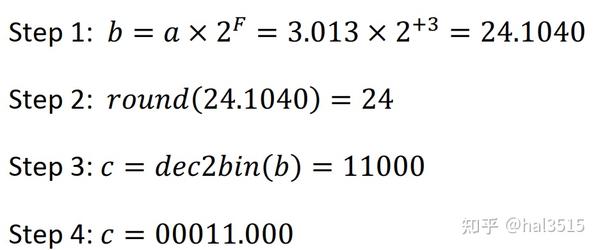FPGA的算法解析3：定点数与浮点数

定点数与浮点数是FPGA数值计算的基础，这里做一下简单的梳理，具体的内容主要是基于 FPGA 的数字信号处理（第二版，高亚军）：这本书讲解比较详细，值得参考。下面这个链接给出了使用 Matlab 完成浮点数定点化的方式。

http://ee.sharif.edu/~digitalvlsi/Docs/Fixed-Point.pdfee.sharif.edu/~digitalvlsi/Docs/Fixed-Point.pdf

（1）浮点数

下面对浮点数的梳理主要根据 IEEE-754 所定义的二进制标准浮点数。这里 $s、m、e$ 分别为符号位、尾数、指数的实际值， $n$ 为相应浮点数的值。

$n=(-1)^{s} \times m \times 2^{e}\\$

更进一步，主要的两种浮点数类型分别是单精度（32位，对应于C语言中的float）、双精度（64位，对应于C语言中的double）。

1、单精度浮点数

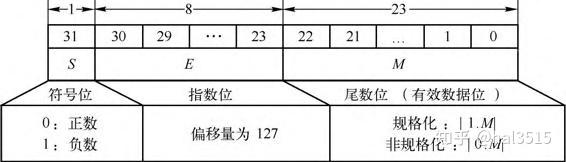
单精度浮点数的符号数 1 位，指数位 8 位，有效数据位 23 位。单精度浮点数又分为规格化与非规格化：

规格化：当 E 所表示的二进制序列不全为 0 也不全为 1 。

$n=(-1)^{S} \times|1 . M| \times 2^{|E|-127} \\$

例如 s = 0，E＝10001000， M＝10010…0（省略部分为0）

$n=(-1)^{0} \times|1 . 5625| \times 2^{|136|-127} = 800\\$

由于 E 所表示的二进制序列不全为 0 也不全为 1，故 0＜|E|＜255，因此 -127<|E| - 127<128 。尾数的实际值 m 的最小值为 1（M 全为 0），最大值为 $2-2^{-23}$ （M全为1）。规格化浮点数所能表示的数的绝对值最大值为 $(2-2^{-23} )×2^{127}$ ，以十进制科学计数法表示为 $3.4×10^{38}$ ，此时M全为1，|E|＝254；最小为 $1.0×2^{-126}$ ，以十进制科学计数法表示为 $1.2×10^{-38 }$ ，此时M全为0，|E|＝1。

非规格化：当E的二进制位全部为0时。

$n=(-1)^{S} \times|0 . M| \times 2^{-126}\\$

把 M 所有位置为 0，就可以表示数 0，将 M 所有位置为 1，就可以表示数 $1- 2^{-23}$ 。非规格化浮点数所能表示的数的绝对值最大值为 $(1-2^{-23} )×2^{-126}$ ，最小为 0 。

特殊数值：

当 $|E| = 255$ ， $|M| = 0$ 时表示无穷大。
当 $|E| = 255$ ， $|M| \ne 0$ 时表示不合法数值。

2、双精度浮点数

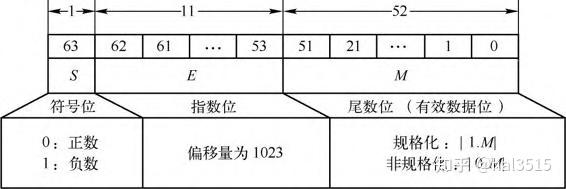
双精度浮点数的符号数 1 位，指数位 11 位，有效数据位 52 位。

规格化：当 E 所表示的二进制序列不全为 0 也不全为 1 。

$n=(-1)^{S} \times|1 . M| \times 2^{|E|-1023} \\$

规格化浮点数所能表示的数的绝对值最大值为 $(2-2^{-52} )×2^{1023}$ ，以十进制科学计数法表示为 $1.8×10^{308}$ ，最小为 $1.0×2^{-1022}$ ，以十进制科学计数法表示为 $2.2×10^{-308 }$ 。

非规格化：当E的二进制位全部为0时。

$n=(-1)^{S} \times|0 . M| \times 2^{-1022}\\$

把 M 所有位置为 0，就可以表示数 0，将 M 所有位置为 1，就可以表示数 $1- 2^{-52}$ 。非规格化浮点数所能表示的数的绝对值最大值为 $(1-2^{-52} )×2^{-1022}$ ，最小为 0 。

特殊数值：

当 $|E| = 2047$ ， $|M| = 0$ 时表示无穷大。
当 $|E| = 2047$ ， $|M| \ne 0$ 时表示不合法数值。

3、浮点数运算

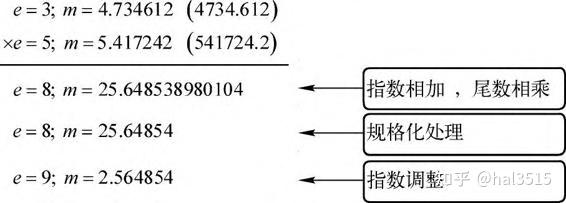
加法：

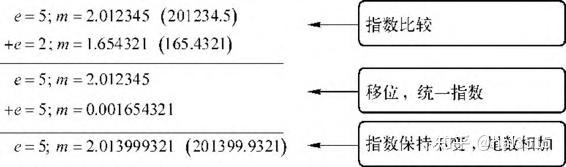
乘法：

（2）定点数

定点数中小数点的位置由两个参数确定，一个是定点数的位宽 $w$ ，小数位的位宽 $wf$ 。

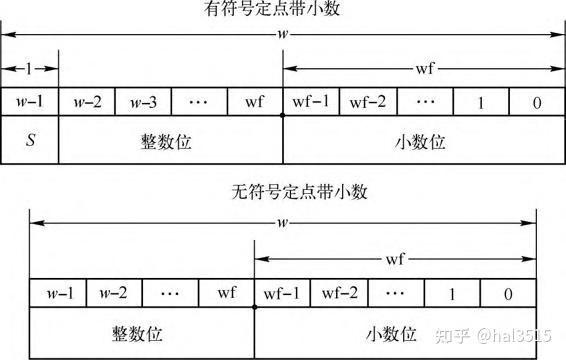
有符号定点带小数：下面给出有符号定点数的值，下面 $b_i$ 表示对应位的数值。

$v=(-1)^{b_{w-1}} 2^{w-1-\mathrm{wf}}+\sum_{0}^{w-2} 2^{i-\mathrm{wf}} b_{i}\\$

无符号定点带小数：下面给出无符号定点数的值，下面 $b_i$ 表示对应位的数值。

$v=\sum_{0}^{w-1} 2^{i-\mathrm{wf}} b_{i}\\$

定点数的表示法

XQN 表示法：XQN 可以表示成 1+X+N ，1 表示符号位，X 表示整数位总位数，N 表示小数总位数。XQN 可以表示 $-2^X\sim2^X-2^{-N}$ 。
System Generator Fix format ：定义为Fixword_length_fractional_length，Fix(1+X+N)_N。

下面给出一个例子，2Q6（Fix9_6）

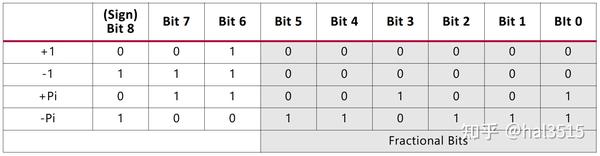
2Q6 包含一个 1 个符号位，2 个整数位，6 个小数位。 $-\pi \approx -2^{2} + 2^{-1} + 2^{-2} + 2^{-4} + 2^{-5} + 2^{-6} = -3.140625\\$

（3）浮点数与定点数的比较

1、浮点数的优势

更宽的动态范围。
可缩短复杂算法的开发周期：采用浮点数由于其较宽的动态范围可以满足绝大多数场合的需求，较少碰到溢出的问题，因此在复杂算法开发中可以省去处理溢出问题的这些时间。
统一的标准数据格式：采用定点数运算时，为满足动态范围或精度要求，算法中的某些操作需要增加字长，某些操作需要减少字长，从而使得定点数的格式根据需求而变化，就会出现一个设计中有不同的定点数格式。而浮点数采用了单精度或双精度，这也增强了代码的复用性，降低了算法建模的复杂度。

2、定点数的优势

消耗资源相对较小，并且计算速度相对浮点数更快。

从应用场合来看，很多场合采用定点数即可满足系统性能需求，但有些场合对精度要求很高，如雷达成像、医学成像、高性能计算等需要采用浮点数。

（4）浮点数到定点数的转换

可利用 Matlab 函数 fi 完成浮点到定点的转换。

% v — Value：fi 对象的值，指定为标量、向量、矩阵或多维数组。  
% s — Signedness：值为1或true表示有符号数据类型，值为0或false表示无符号数据类型。  
% w — Word length：字长，单位是 bit
% f — Fraction length：小数的长度，单位是 bit
a = fi(v,s,w,f)
a = fi(pi,1,8,3)
a = 3.1250
    DataTypeMode: Fixed-point: binary point scaling
    Signedness: Signed
    WordLength: 8
    FractionLength: 3

另一种方法，考虑一个浮点数 a ，依据以下 4 步可以完成浮点向定点的转换：

Step1：计算 $b = a \times 2^F$ ， F 表示小数的字长。
Step2：将 b 转换成最近的整数，例如 round(3.56) = 4，round(-1.9) = -2。
Step3： 将 b 用二进制表示成 c。
Step4：假定 c 用 n 位表示 b。w 表示最终的定点数的字长，f 表示最终的定点数的小数长度。w 应当不小于 n，最终的数最左边（w-n）位补零，小数部分选取 c 的最低 f 位。

下面给一个例子，假设 a = 3.103，w = 8，f = 3。

posted on 2022-06-20 10:11 皮皮祥阅读(654) 评论(0) 编辑收藏举报

刷新页面返回顶部

皮皮祥的博客

导航

公告