数学运算(五)——定点数和科学计数的四则运算
数学运算(五)——定点数和科学计数的四则运算
数学运算(六)——矩阵计算(待更)
数学运算(七)——通用非线性函数计算(待更)
数学运算(八)——通用非线性函数的CORDIC方法(待更)
本系列学习自《IP核芯志》

讲了这么半天的整数运算,今天来点不一样的。小数运算。
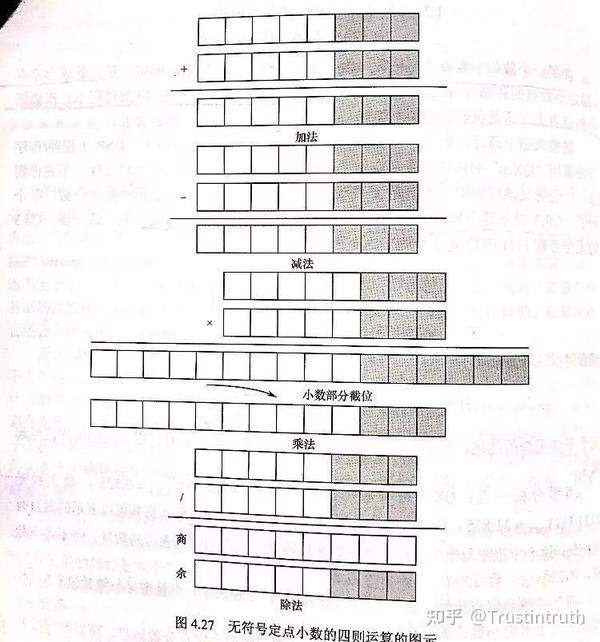
首先定点数就是用整数来表示小数。因为小数点是确定的,所以可以把小数点忽略不存储。对于无符号定点小数的加法和减法运算时,直接按照整数计算即可,小数实际上只存在在设计者心中。而乘法需要左移一个小数位的宽度,除法也可以不会管小数,毕竟小数点后面的尾数相同,就都等于成了一个十的负(小数位数)次方。放一个图大家就很好理解了
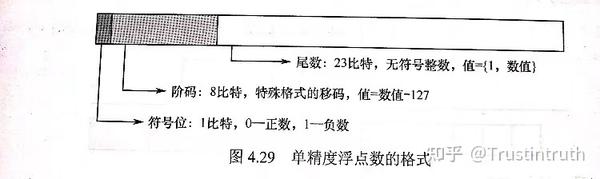
其实定点数真的很简单,所以我们来聊一聊浮点数。IEEE754中规定了多种浮点数精确格式,包括单精度双精度和扩展双精度。一般来说,单精度符号位1bit,阶码8bits,尾数23bits。高标准规定基数为2,阶码用移码表示,尾数用原码表示。数值的最高位默认是1,所以位数的表示范围比实际存储要多一位。如果阶码为0并且尾数也是0,那么这个数的真值为 。如果阶码是255并且尾数是0,马me这个数的真值为
。如果阶码是255并且尾数不是零,那么这不是一个数(NaN)如果觉得这段话云山雾罩(最近看相声看多了,老想这个词)的话,我就要请出第二幅图了
说完了IEEE754,就要好好说一说浮点数加减法操作
相较于定点数的加减直接做,浮点数的加减法不不能是简简单单的把尾数加一起就得了,要考虑阶码。浮点数加减法法的实现方法就是以绝对值大的数字为基准(为什么?因为在后面运算时要进行移位操作,较小数右移实际上就是在舍弃低位。要是让较大数左移不就舍弃高位了吗?),移动绝对值小的数字,然后做加减。所以我们设计的模块要比较大小,要选择减数和被减数,要选择符号,要选择阶码和符号还要移位尾数相加。设计如图:
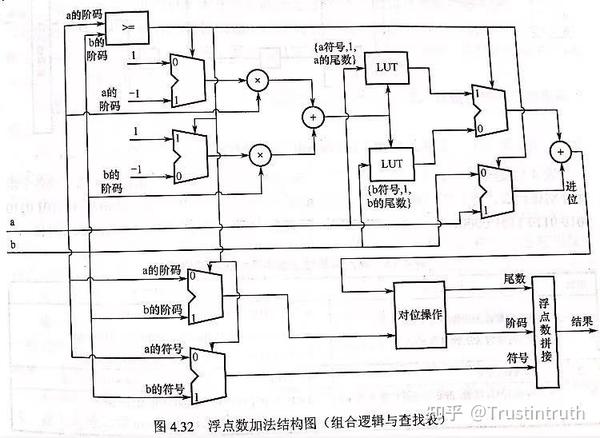
这里,书中特别提醒了一下,由于上述加法是移位后再加,这里会有人这样写
assign y = x >> v ;
这种写法是不可综合的,因为一般的assign语句中x和y都是可变的,但是v是不可以的!我们可以使用case语句来实现:
case v:
6'h00 : y <= x ;
6'h01 : y <= x >>1 ;
……
6'h31 : y <= x >> 8 ;
default : y <= 31'h0 ;
其实代码中default里面的内容,就是位置给到了0.这是因为阶数相差过大了,较小数不能影响较大数的运算了。
但是这种设计的工作时钟频率不会太高,所以我们进行优化,上流水,再进行优化。
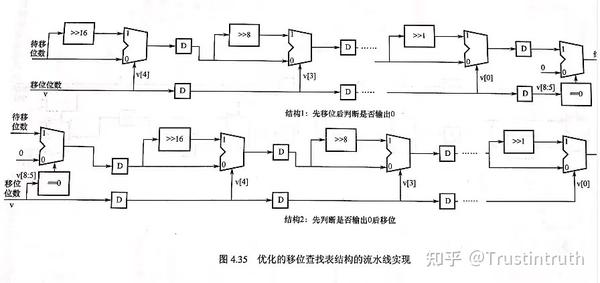
说完加减说乘除,乘法其实很简单,尾数进行乘法运算,阶数进行加法运算。这里注意两件事:1.银行的首位“1”必须要加上。2.尾数是定点数的分数,需要注意结果的小数点的位置。浮点数乘法的主要结构是