Python：层次聚类分析——基于基站定位数据商圈分析

《Python数据分析与挖掘实战》书中本章无原始数据，文中仅展示了聚类分析了各人群聚集区特征（商圈特征，做营销策划住宅区、CBD商场、办公楼这还用聚类分析吗，直接肉眼也能辨别吧，这就是所有的人流特征和规律？）也是没什么实际用处，而且数据源数据预处理过程才是挖掘重点吧，避重就轻。

记录学习一下两点

  • 数据标准化方式（归一化、标准化、正规化）
  • 聚类分析算法

归一化：无量纲化，提升模型的收敛速度、精度；需考虑标准化前后模型是否同解等价

正则化：一般是为解决模型过拟合问题，除降低特征维度外可选用的方法就是给模型目标函数加入正则化项（即惩罚项，如L1范数（如Lasso），L2范数（如ridge））

 

数据标准化 

离差标准化（0-1标准化/max-min标准化）

 

Z标准化（标准差标准化，Z-score标准化）

 

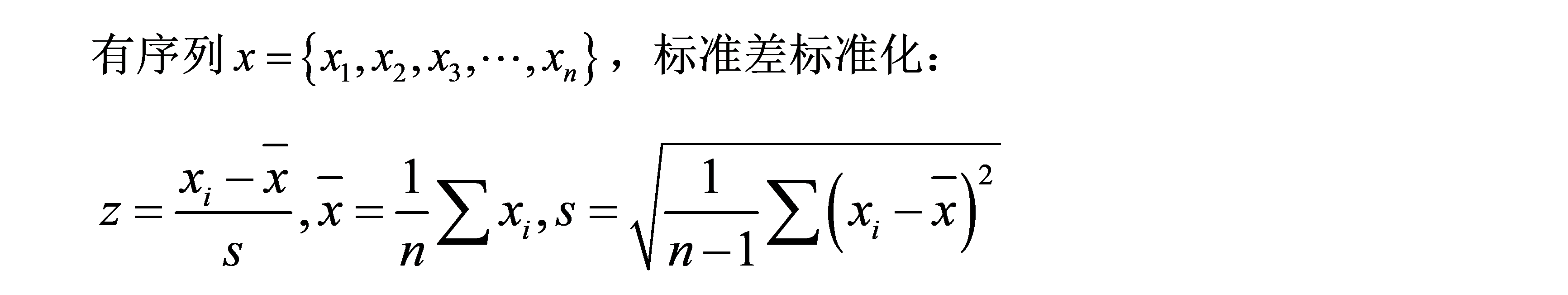
 小数定点标准化，归一化

 

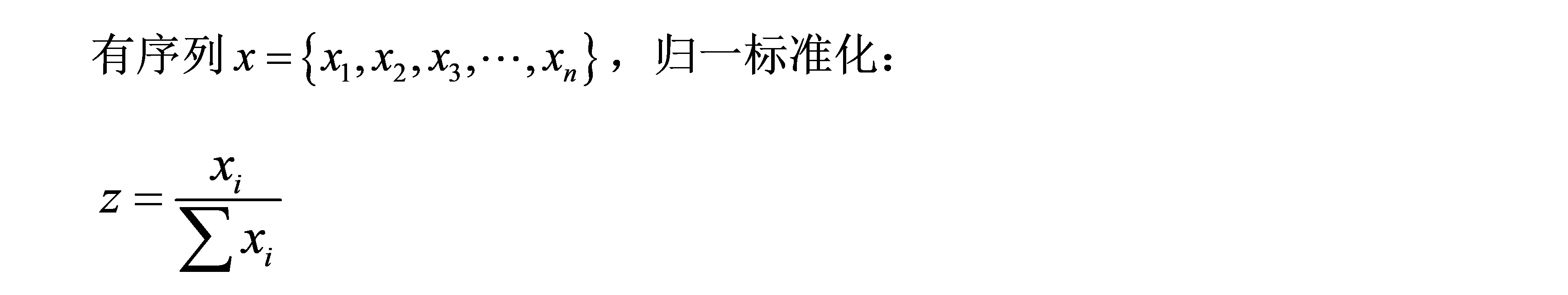
 聚类分析算法

比较经典的有k-means和层次聚类法。

 

层次聚类法

层次聚类法基本过程如下：

  • 每一个样本点视为一个簇；
  • 计算各个簇之间的距离，最近的两个簇聚合成一个新簇；
  • 重复以上过程直至最后只有一簇。

层次聚类不指定具体的簇数，而只关注簇之间的远近，最终会形成一个树形图。

sklearn模块中

1 from sklearn.cluster import AgglomerativeClustering as AC 
2 #sklearn.cluster.AgglomerativeClustering(n_clusters=2, affinity='euclidean', memory=None, connectivity=None, compute_full_tree='auto', linkage='ward')
3 #affinity距离算法
4 #linkage合并的策略
5 model=AC(n_clusters=3,linkage='ward')
6 #linkage : {“ward”, “complete”, “average”}, optional, default: “ward”
7 # “euclidean”, “l1”, “l2”, “manhattan”, “cosine”, or ‘precomputed’. If linkage is “ward”, only “euclidean” is accepted
8 model.fit(data_normal)

 

 linkage criteria 确定用于合并的策略的度量:

  • Ward 最小化所有聚类内的平方差总和。这是一种 variance-minimizing （方差最小化）的优化方向， 这是与k-means 的目标函数相似的优化方法，但是用 agglomerative hierarchical（聚类分层）的方法处理。
  • Maximum 或 complete linkage 最小化聚类对两个样本之间的最大距离。
  • Average linkage 最小化聚类两个聚类中样本距离的平均值。

scipy模块中

 

from scipy.cluster.hierarchy import linkage,dendrogram  # scipy中的层次聚类

Z=linkage(data_normal,method='ward',metric='euclidean')
#method={ ‘single’,‘complete’, ‘average’, ‘weighted’, ‘centroid’, ‘median’,‘ward’ }
#metric={ ‘braycurtis’, ‘canberra’, ‘chebyshev’, ‘cityblock’, ‘correlation’, ‘cosine’, ‘dice’, ‘euclidean’, ‘hamming’, ‘jaccard’, ‘kulsinski’, ‘mahalanobis’, ‘matching’, ‘minkowski’, ‘rogerstanimoto’, ‘russellrao’, ‘seuclidean’, ‘sokalmichener’, ‘sokalsneath’, ‘sqeuclidean’, ‘yule’}
P=dendrogram(Z,0) #系统树图
plot.show()  # 画出聚类图

  

K-means聚类法

 k-means通常被称为 Lloyd’s algorithm（劳埃德算法），其中的k就是最终聚集的簇数。k-means基本过程如下：

  • 首先任取（你没看错，就是任取）k个样本点作为k个簇的初始中心；
  • 对每一个样本点，计算它们与k个中心的距离，把它归入距离最小的中心所在的簇；
  • 等到所有的样本点归类完毕，重新计算k个簇的中心；
  • 重复以上过程直至样本点归入的簇不再变动。

 sklearn模块中

1 sklearn.cluster.KMeans(n_clusters=8, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='auto', verbose=0, random_state=None, copy_x=True, n_jobs=1, algorithm='auto')
2 
3 from sklearn.cluster import KMeans
4 kmeans = KMeans(n_clusters=2, random_state=0).fit(X)
5 kmeans.labels_ #kmeans[1]
6 kmeans.cluster_centers_  #kmeans[0]

 

 scipy模块中

 

from scipy.cluster.vq import vq, kmeans, whiten

whitened = whiten(features)
# kmeans聚类前对每个属性特征标准化，除以各自标准差（列）
codebook, distortion = kmeans(whitened, 2) # 标准化后数据及需要聚成类个数
# 返回两个量分别是类中心和损失
label=vq(whitened,codebook)[0] #vq函数根据聚类中心对所有数据进行分类,[0]表示返回两维中的类别

 本文用到代码比较简短，附于此以作记录

 

 1 # -*- coding: utf-8 -*-
 2 """
 3 Created on Mon Oct  1 00:20:30 2018
 4 
 5 @author: Luove
 6 """
 7 
 8 import os
 9 import pandas as pd
10 import numpy as np
11 from scipy.cluster.hierarchy import linkage,dendrogram  # scipy中的层次聚类
12 from sklearn.cluster import AgglomerativeClustering as AC  # sklearn中的层次聚类
13 import matplotlib.pyplot as plt
14 import scipy.cluster.vq
15 os.getcwd()
16 os.chdir('D:/Analyze/Python Matlab/Python/BookCodes/Python数据分析与挖掘实战/图书配套数据、代码/chapter14/demo/code')
17 filepath='../data/business_circle.xls'
18 
19 data=pd.read_excel(filepath)
20 data.head()
21 data=data.iloc[:,1:]
22 data_normal=(data-data.min())/(data.max()-data.min())  # 离差标准化
23 
24 Z=linkage(data_normal,method='ward',metric='euclidean')
25 P=dendrogram(Z,0)
26 plot.show()
27 
28 model=AC(n_clusters=3,linkage='ward')
29 model.fit(data_normal)
30 data_1=pd.concat([data_normal,pd.Series(model.labels_,index=data.index)],axis=1)
31 data_1.columns=list(data_normal.columns)+['聚类类别']
32 data_1.shape
33 # 正确显示 中文及负号
34 plt.rcParams['font.sans-serif']=['SimHei']
35 plt.rcParams['axes.unicode_minus']=False
36 
37 style=['bo-','ro-','go-']
38 xlabels=['工作日人均停留时间','凌晨人均停留时间','周末人均停留时间','日均人流量']
39 
40 for i in range(3):
41     plt.figure()
42     tmp=data_1[data_1['聚类类别']==i].iloc[:,:4]
43     for j in range(len(tmp)):
44         plt.plot(range(1,5),tmp.iloc[j,:],style[i])
45     plt.xticks(range(1,5),xlabels,rotation=20)
46     plt.subplots_adjust(bottom=0.15)
47

 

 

 

 

 

Ref：

 

三种常用数据标准化方法

数据标准化/归一化normalization

聚类分析：k-means和层次聚类

关于聚类及相似度、距离的知识点及kmeans聚类介绍 

使用scipy进行层次聚类和k-means聚类

K均值聚类和矢量量化（scipy.cluster.vq）

sklearn.cluster.KMeans

sklearn.cluster.AgglomerativeClustering

 

《数据分析与挖掘实战》：源代码及数据需要可自取：https://github.com/Luove/Data

 

posted @ 2018-10-01 04:24  Luove  阅读(3147)  评论(0)  编辑  收藏  举报