Python:Lasso方法、GM预测模型、神经网络预测模型之财政收入影响因素分析及预测
问题重述
通过研究,发现影响某市目前及未来地方财源的因素。结合文中目标:(1)选择模型,找出影响财政收入的关键因素;(2)基于关键因素,选择预测方法、模型预测未来收入。
具体来讲
本文分析了地方财政收入、增值税收入、营业税收入、企业所得税收入、个人所得税收入的影响因素并对未来两年采用灰色预测(GM(1,1))并以已有年度序列训练神经网络(NN),再以得到的模型预测包括未来两年在内的所有年份收入的预测值,由此可以根据预测相比于实际值情况及未来收入变化作出相应的决策判断。
文中的操作流程步骤非常值得学习,思路很清晰(实际类似问题可类比此类框架):
- 从统计局网站及各统计年鉴搜集该市财政收入及各类别收入相关数据;
- 数据预处理,得到建模用数据,构建LassoLars变量选择模型;
- 根据所选择变量建立单变量GM(1,1)Model预测该变量序列下年值,及根据所选变量(特征变量)及收入(类变量,标签变量)构建人工神经网络模型(训练模型)
- 将由GM(1,1)得到的个所选变量的预测值数据所得到的神经网络(模型预测),从而得到各种收入的预测值
方法、模型及代码
Lasso方法:
线性回归的L1正则化通常称为Lasso回归,一般来说,对于高维的特征数据,尤其线性关系是稀疏的,我们会采用Lasso回归。或者是要在一堆特征里面找出主要的特征,那么Lasso回归更是首选了。Lasso回归的损失函数优化方法常用的有两种,坐标轴下降法和最小角回归法(Least Angle Regression)。Lasso类采用的是坐标轴下降法,这里LassoLars模型采用的是最小角回归法。详细介绍参见文末Ref。
1 #导入使用的模块 2 import os 3 import numpy as np 4 import pandas as pd 5 from sklearn.linear_model import LassoLars 6 from sklearn.linear_model import Lasso 7 from keras.models import Sequential #有的同学可能会遇到 kernel died,restarting的问题,可参见我的另一片文章 8 from keras.layers.core import Dense, Activation 9 import matplotlib.pyplot as plt 10 #import tensorflow as tf 11 12 # 13 filepath='../data/data1.csv' 14 data=pd.read_csv(filepath) 15 des=data.describe() 16 r=des.T 17 r=r[['min','max','mean','std']] 18 np.round(r,2) # 保留2位小数,四舍六入五留双(五留双即遇五看五前面是偶数则保留,奇数进位) 19 #np.round([0.15,0.25,0.14,0.16],1) # array([0.2, 0.2, 0.1, 0.2]) 20 np.round(data.corr(method='pearson'),2) # method={'pearson','spearman','kendall'},计算相关系数,相关分析 21 22 model = LassoLars(alpha=1) # LASSO回归的特点是在拟合广义线性模型的同时进行变量筛选和复杂度调整,剔除存在共线性的变量 23 model.fit(data.iloc[:,:data.shape[1]-1],data.iloc[:,data.shape[1]-1]) 24 #pd.DataFrame(model.coef_,columns=['x%d' %i for i in np.arange(13)+1]) 25 model_coef=pd.DataFrame(pd.DataFrame(model.coef_).T) 26 model_coef.columns=['x%d' %i for i in np.arange(13)+1] 27 model_coef 28 #由系数表可知,系数值为零的要剔除,得到特征变量'x3','x5','x7','x11'
GM-Model
GM-Model即灰色预测模型,灰色预测法是一种预测灰色系统的预测方法。灰色预测通过鉴别系统因素之间发展趋势的相异程度,即进行关联分析,并对原始数据进行生成处理来寻找系统变动的规律,生成有较强规律性的数据序列,然后建立相应的微分方程模型,从而预测事物未来发展趋势的状况。
灰色系统相对于白色、黑色系统,白色系统即系统的内部特征是完全已知的,既系统信息是完全充分的;黑色系统系统的内部信息对外界来说是一无所知的,只能通过它与外界的联系来加以观测研究;灰色处于二者之间,部分已知部分未知,系统内各因素间有不确定的关系。
GM(1,1)重要概念
原始序列
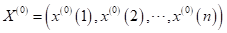
一次累加(1-AGO,Accumulating Generation Operator)及与原序列关系
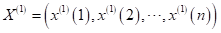
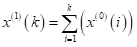
紧邻均值生成(也可加权生成)及与AGO序列关系
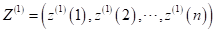

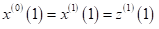
GM(1,1)白化方程
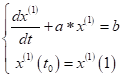
白化方程的解及还原值
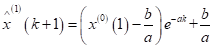
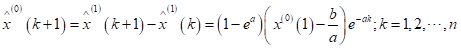
模型检验相关的残差序列

后验差检验中的p和C
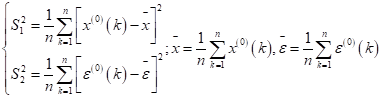
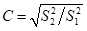
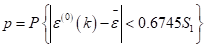
更多详细可参加Ref或自行百度。
后验差检验
指标C(后验差)和p(小误差概率)是后验差检验的两重要指标【和计算得序列对应,非针对模型和某一特定值而是序列】,C越小越好,C越小即原始数据方差大,离散程度大,残差方差越小,离散程度小;C小表明尽管原始数据很离散,而模型所得计算值与实际值之差并不太离散。
指标p越大越好,p越大残差与残差平均值之差小于给定值0.6745的点较多,即拟合值(或预测值)分布比较均匀。
|
模型精度等级 |
均方差比值C |
小误差概率p |
|
1级(好) |
C<=0.35 |
0.95<=p |
|
2级(合格) |
0.35<C<=0.5 |
0.8<=p<0.95 |
|
3级(勉强) |
0.5<C<=0.65 |
0.70<=p<0.8 |
|
4级(不合格) |
0.65<C |
p<0.7 |
模型精度级别=Max(p的级别,C的级别)。
1 # GM模型,预测 2 def GM11(x0): #自定义灰色预测函数 3 import numpy as np 4 x1 = x0.cumsum() #1-AGO序列 5 x1 = pd.DataFrame(x1) 6 z1 = (x1 + x1.shift())/2.0 #紧邻均值(MEAN)生成序列 7 z1 = z1[1:].values.reshape((len(z1)-1,1)) # 转成矩阵 8 B = np.append(-z1, np.ones_like(z1), axis = 1) # 列合并-z1和形状同z1的1值矩阵 19X2 9 Yn = x0[1:].reshape((len(x0)-1, 1)) # 转成矩阵 19 10 [[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Yn) #计算参数,基于矩阵运算,np.dot矩阵相乘,np.linalg.inv矩阵求逆 11 f = lambda k: (x0[0]-b/a)*np.exp(-a*(k-1))-(x0[0]-b/a)*np.exp(-a*(k-2)) #还原值 12 delta = np.abs(x0 - np.array([f(i) for i in range(1,len(x0)+1)])) # 残差绝对值序列 13 C = delta.std()/x0.std() 14 P = 1.0*(np.abs(delta - delta.mean()) < 0.6745*x0.std()).sum()/len(x0) 15 return f, a, b, x0[0], C, P #返回灰色预测函数、a、b、首项、方差比、小残差概率 16 17 #x0=data_1['x3'][:-2].values 18 19 20 21 l=['x3','x5','x7','x11','y'] 22 data_1=data[l].copy() 23 data_1.index=range(1994,2014) 24 data_1.loc[2014]=None # 添加预测行 25 data_1.loc[2015]=None 26 27 for i in l: # 列计算,预测每列2014、2015预测值 28 f=GM11(data_1[i][:-2].values)[0] # 利用返回的灰色预测函数,仅和对对应期数及位置有关 29 data_1[i][2014]=f(len(data_1)-1) 30 data_1[i][2015]=f(len(data_1)) 31 data_1[i]=data_1[i].round(2)
神经网络预测
关于神经网络的文章较多,不展开介绍,主要说明一点书中的代码有点旧keras更新后代码要调整一下。
代码中输出时是没有激活函数的,即直接输出。或者说把激活函数看作f(x)=x。
1 # 预测财政收入,2014、2015(y) 神经网络,用到data_1 2 data_train=data_1.loc[range(1994,2014)].copy() 3 data_train_normal=(data_train-data_train.mean())/data_train.std() # 数据标准化,按列索引(列名)计算 4 y_class=l.pop() 5 x_train=data_train_normal[l] # 特征数据提取 6 y_train=data_train_normal[y_class] #标签数据提取 7 # 构造神经网络模型 8 nn_model=Sequential() # create the NN-model 9 nn_model.add(Dense(input_dim=4,units=12)) # 10 nn_model.add(Activation('relu')) # 11 nn_model.add(Dense(1)) # 最后一层不激活,直接输出。或者说把激活函数看作f(x)=x 12 nn_model.compile(loss='mean_squared_error', optimizer='adam',metrics=['accuracy']) 13 #net.fit(train_data[:,:3],train_data[:,3],epochs=10,batch_size=1)#keras 2.0之前版本 14 nn_model.fit(x_train,y_train,epochs=10000,batch_size=16,verbose=1)#keras 2.0,推荐,verbose=0,不显示过程,默认等于1显示过程 15 # 预测,还原结果 16 x=((data_1[l]-data_train[l].mean())/data_train[l].std()).values 17 data_1['y_pred']=nn_model.predict(x)*data_train['y'].std()+data_train['y'].mean() 18 #ax1=plt.subplot(211) 19 #ax1.plot(data_1['y'],'b-o') 20 #ax1.legend() 21 #ax2=plt.subplot(212) 22 #ax2.plot(data_1['y_pred'],'r-*') 23 #ax2.legend() 24 #plt.show() 25 plt.plot(data_1['y'],'b-o') 26 plt.plot(data_1['y_pred'],'r-*') 27 plt.legend() 28 # 政府性基金收入采用GM11预测2006-2015年份收入,并和原值2006-2013比较 29 x0 = np.array([3152063, 2213050, 4050122, 5265142 ,5556619, 4772843, 9463330]) 30 f, a, b, x00, C, P = GM11(x0) # 得到预测函数f,可计算接下来预测值(和序号相关,按序预测) 31 len(x0) 32 print('2014、2015年预测结果分别是:%.2f和%.2f'%(f(len(x0)+1),f(len(x0)+2))) 33 print('x0序列的后验差比值为%.2f'%C) 34 35 p=pd.DataFrame(x0,index=range(2007,2014),columns=['y']) # 'y'要带上中括号 36 p.loc[2014]=None 37 p.loc[2015]=None 38 p['y_pred']=[f(i+1) for i in range(len(p))] 39 p=p.round(2) 40 p.index=pd.to_datetime(p.index,format='%Y') 41 #for i in range(len(p)): 42 # print(i+1) 43 plt.plot(p['y'],'b-o') 44 plt.plot(p['y_pred'],'r-*') 45 plt.legend() 46 #plt.show()
输出图形:
上图为财政收入预测(其中y的2014、2015值是GM(1,1)预测结果)
下图为政府性基金收入预测
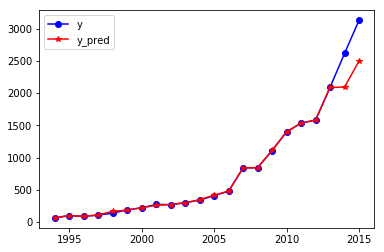
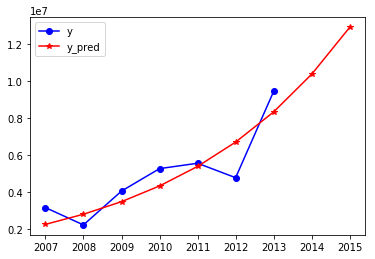
注:以上仅以财政收入分析为例,其余方法完全一致,政府性基金收入与其他不同采用的是单序列单变量GM模型(即GM(1,1)),相比原序列很平滑可以看出趋势,二者均有稳中有升的趋势。
Ref:
scikit-learn实现线性回归之Lassolars模型
《数据分析与挖掘实战》源代码及数据需要可自取:https://github.com/Luove/Data

 浙公网安备 33010602011771号
浙公网安备 33010602011771号