Sequential Recommendation via Stochastic Self-Attention阅读笔记

动机

本文是2022年WWW的一篇论文。序列推荐中有类种方法是基于transformer的，它用向量表示一个物品并利用点积计算两个物品之间的相似程度。用户的兴趣通常是通过它的交互序列表示的，之前的工作是通过一个确定的向量表示用户的兴趣，但是用户实际的交互序列是不确定的（这里我的理解是用户的兴趣并不确定，直接用一个向量表示会出现不能充分表达用户兴趣的情况），直接用上述方式很难捕获到协同传递性。作者提出了一种随机自注意力模型(STOSA)解决上述问题，将物品用随机高斯分布表示，并且在BPR损失中加入正则化约束正项和负项的关系。

算法

模型整体结构如图，首先将物品表示为多维椭圆高斯分布的embedding，其中包括平均embedding和协方差embedding(平均embedding可看作基础兴趣，协方差embedding可看作变化兴趣)，之后通过一个基于Wasserstein距离的自注意力层计算不确定序列的embedding，最后通过向BPR损失中加入正则化，使得正项和负项之间的距离增大。

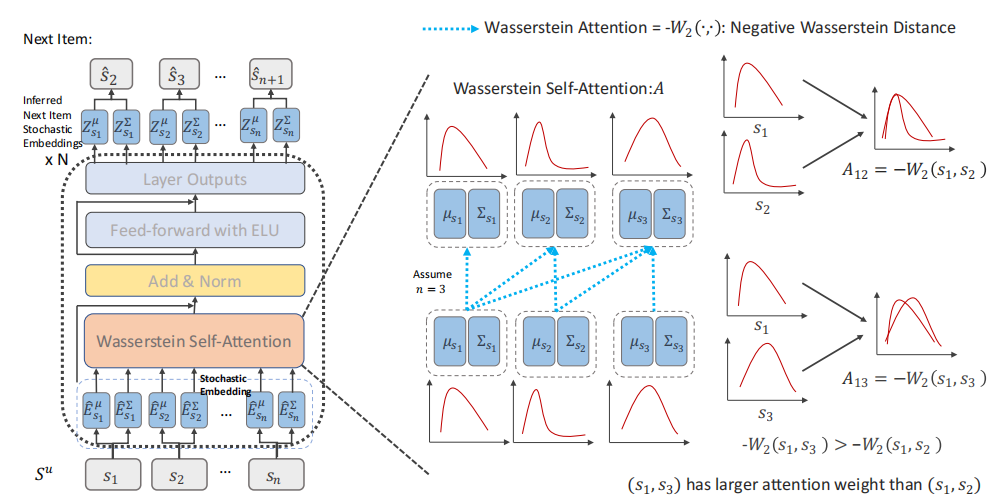
随机嵌入层

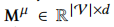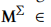
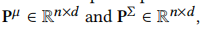作者使用多维椭圆高斯分布表示物品embedding，使物品覆盖更广的空间，拥有更多协作邻居。用表示平均embedding，表示协方差embedding。分别表示均值和协方差的位置embedding。我们可以得到用户u的平均和协方差序列embedding

Wasserstein自注意力层

令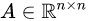表示自注意力的值，\(A_{kt}\)表示位置k的物品和位置t的物品的注意力分数，k<=t

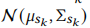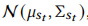这里点积不适合计算分布之间的差异，这里使用Wasserstein距离计算，上述两个物品分布分别为和。其中，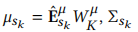
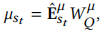
我们使用2-Wasserstein距离计算注意力权重

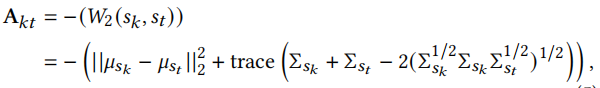
这里使用Wasserstein距离是因为：1.Wasserstein距离用于测量分布之间的距离。2.它可以捕获序列中的协同传递性，一定程度上解决冷启动问题。3.使训练过程更稳定。
Wasserstein注意力聚合，将注意力权重归一化后对embedding加权求和


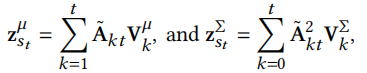
其中

前馈网络和输出

这里公式就可以很容易看懂，前馈网络

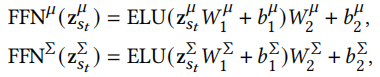
输出

这些输出Z组成的新序列可作为下一个Wasserstein自注意力层的输入。

预测层

在得到最终输出后，对于位置t的物品\(s_t\)和位置t+1的物品j，使用2-Wasserstein计算它们之间的距离

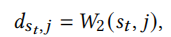
其中，，，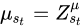

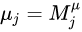损失函数

本文使用标准BPR损失函数，但是标准BPR损失函数没有考虑到正样本和负样本之间的距离，因此我们添加正则化来增大其之间的距离

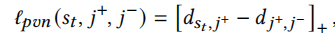
其中[x]=max(x,0)，\(j^+\)是实际的下一个物品，\(j^-\)是采样的负样本。总的损失函数为

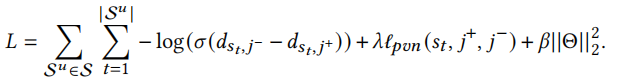
结果

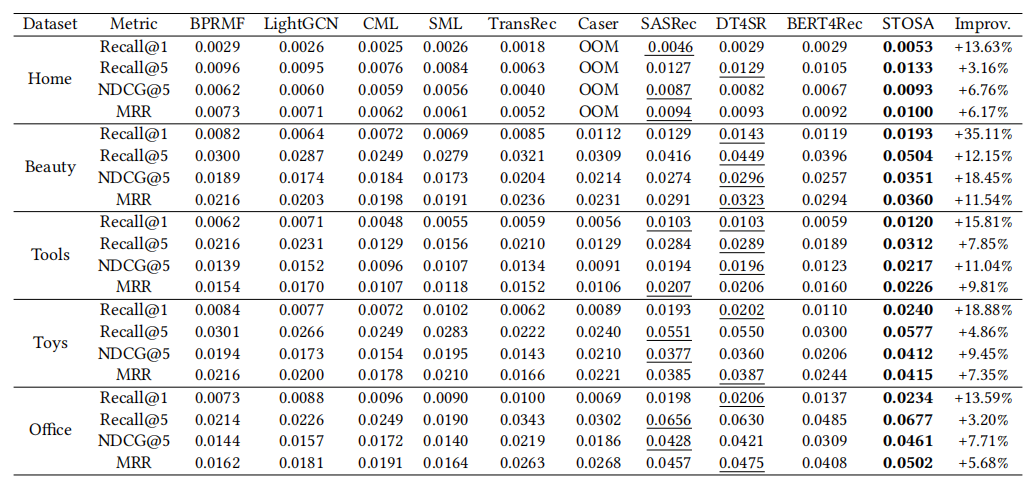
作者在亚马逊的五个数据集上测试，与基线模型相比，本文提出的STOSA均取得最好效果。

总结

本文的创新点主要是在序列推荐中，使用了Wasserstein Self-Attention，从衡量向量之间的距离转变为衡量分布之间的距离。最后向BPR loss加入的正则化是为了增大正项与负项之间的距离，这一点我觉得和对比学习应该是有类似的效果的，不确定对比学习方法是否可以应用在本文中，如果以后有机会复现本论文，会尝试用对比正则化。