Neural Collaborative Filtering阅读笔记
动机
本篇论文是2017年IW3C2上的一篇论文。在当时深度神经网络已经在计算机视觉、自然语言处理等领域取得巨大成功,但是却很少应用在推荐系统中。虽然当时也有一些工作采用深度学习来进行推荐,但它们主要是用深度学习为辅助信息建模,例如项目的文本描述等等。在涉及到协同过滤推荐算法中用户与物品的交互中,这些工作仍然使用矩阵分解并将用户和物品的隐向量内积。由于隐向量内积这一方法过于简单,难以发现用户和物品之间更深的关系,对此,本篇论文提出了一种称为NCF(Neural network based Collaborative Filtering)的通用框架,该框架可以从数据中学习任意函数,捕捉到更深层的用户与物品之间的关系,具有很强的灵活性和表达能力。该框架主要针对隐反馈数据。
算法
基本框架
NCF的框架如下图所示,首先输入的是用户和物品的特征向量(可以采用one-hot编码),之后输入经过Embedding层由稀疏的向量投影为稠密的向量,之后用户的embedding和物品的embedding输入到一个多层的神经网络结构中,最终输出层输出预测的分数。该算法的核心就是学习到一个能挖掘出更深层的用户和物品的关系的函数。
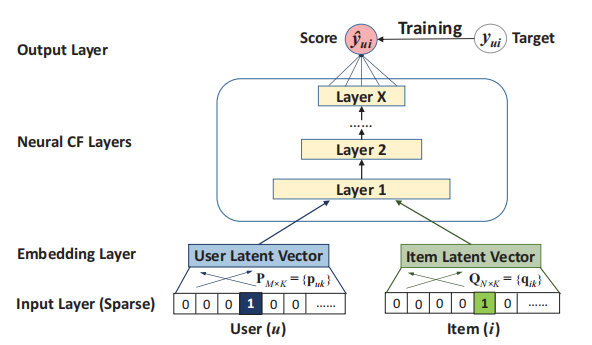
我们可以将该问题看做一个二分类问题,即预测某一个用户与某一个物品是否会有交互,则该框架的损失函数为
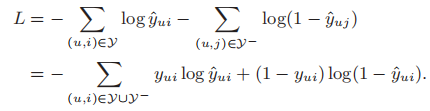
其中集合\(\mathcal{Y}\)表示可以观测到的数据,即意味着该用户与该物品有交互,\(\mathcal{Y}^{-}\)表示缺失的数据,\(y^{ui}\)表示实际的数据,\(\hat{y}^{ui}\)表示预测的数据,1表示可以观测到,0表示观测不到(即缺失)。
框架的三个实例化
Generalized Matrix Factorization (GMF)
矩阵分解(MF)可以看作是NCF框架的一种特例,我们假设\(p_{u}\)为用户的隐向量,\(q_{i}\)为物品的隐向量,神经协同过滤层的映射函数为
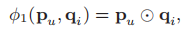
其中\(\bigodot\)表示两个向量对应的元素相乘,将其输入到output层
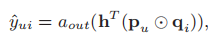
\(a_{out}\)表示的是激活函数,h表示的是边权重。如果我们设置\(a_{out}\)为恒等函数,h为元素都是1的均匀向量,那么我们就可以准确地还原MF模型。
在本次工作中,我们使用sigmoid函数作为激活函数\(a_{out}\),利用对数损失学习h,以上就是GMF的描述。
Multi-Layer Perceptron (MLP)
在此方法中,我们将用户向量\(p_{u}\)和物品向量\(q_{i}\)连接在一起,并且在连接的向量上添加隐藏层,使用MLP学习用户和物品潜在特征之间的交互。
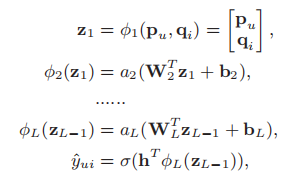
其中\(W_{x},b_{x},a_{x}\)分别表示第x层的权重矩阵,偏置向量和激活函数。激活函数选择ReLU,因为Sigmoid和tanh会出现梯度消失的问题。
Fusion of GMF and MLP(NeuMF)
在第三个实例化中,我们尝试融合上述的GMF和MLP方法。因为对于GMF和MLP这两个模型,它们的最佳embedding大小很可能有很大差别,如果强行让它们的embedding大小相等,最终效果会较差。因此,我们允许这两个模型分别学习它们的embedding层,并通过连接最后一个隐藏层来组合这两个模型,如下图。
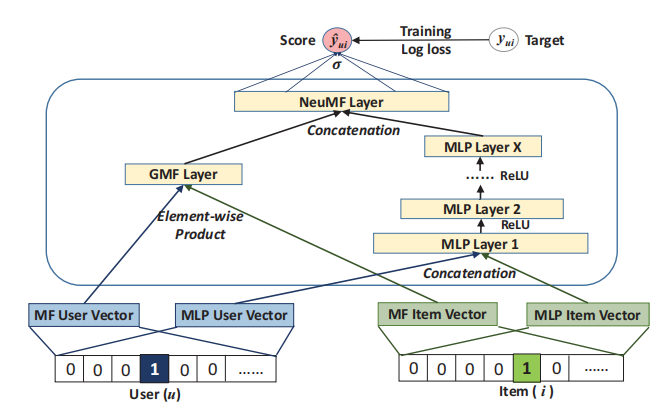
方程如下
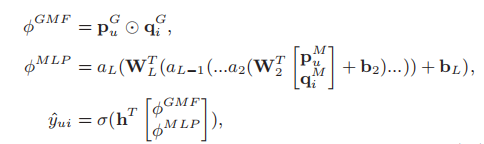
其中\(p^{G}_{u}\)和\(p^{M}_{u}\)分别表示GMF和MLP的用户的embedding,同理\(q^{G}_{i}\)和\(q^{M}_{i}\)为GMF和MLP的物品的embedding。
我们可以使用预训练的GMF和MLP模型去初始化融合后的模型,只需要调整h为
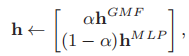
其中\(h^{GMF}\)和\(h^{MLP}\)分别表示预训练好的GMF和MLP中的h,α是权衡两个模型的超参数。
结果
作者提出三个问题,并且以回答作为本次实验的结果。
- Q1:我们的NCF模型是否超越了当前最先进的隐反馈协同过滤方法?
- A1:在本文中的实验中是的。本次选择MovieLens和Pinterest数据集,使用HR和NDCG为评测标准,将本文中实例化的三个方法与ItemPop、ItemKNN、BPR、eALS方法相比,其中NeuMF,即GMF和MLP的融合模型,取得了最好的结果。
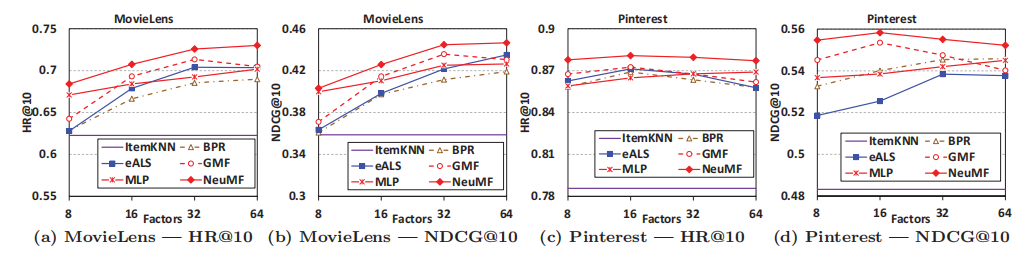
- Q2:我们提出的优化框架如何为推荐系统工作?
- A2:我们将推荐任务转为二分类任务,并且使用对数损失函数进行优化。由下图实验结果可以看出,初期随着损失下降,我们的推荐系统性能上升,但是过多的训练会出现过拟合现象,反而导致推荐性能下降。
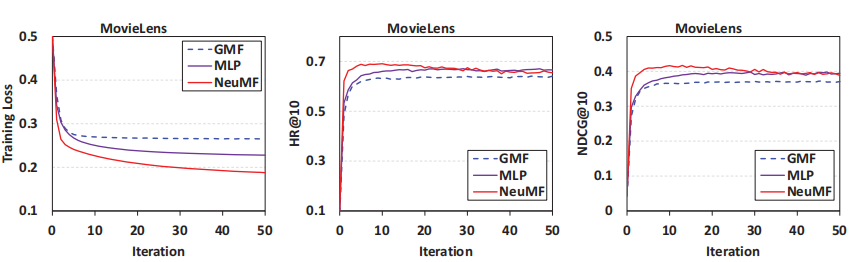
- Q3:更深层的网络是否有助于学习用户和物品交互数据?
- A3:通常情况下,更深层的网络可以带来更好的推荐性能。如下图所示,即使是具有相同能力的模型(文章中提到模型的能力由最后一个隐藏层的维度决定),通常来说,堆叠更多的层可以提高模型的性能。MLP-0代表没有隐藏层,评价指标是HR。
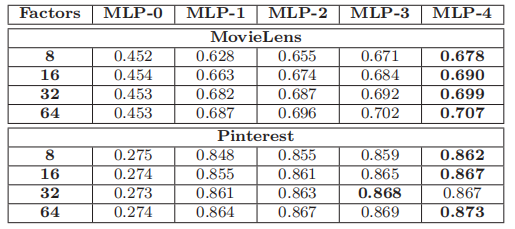
展望
文章中提出了之后的工作会研究RNN在推荐系统中的应用,因为这篇文章已经是四年前的,所以相对于现在来说,方法可能会有些过时。目前较为流行的Attention机制也应该可以应用在推荐系统中,之后我会找一些相关的文献去阅读。


