Probabilistic Matrix Factorization with Non-random Missing Data阅读笔记

动机

本篇论文是出自2014年ICML的一篇论文，矩阵分解模型在协同过滤的方法中表现出卓越的性能，这些模型通常都是假设数据是随机缺失(MAR)的，但是现实生活中常常不是这样，例如部分用户会只给自己喜欢或者讨厌的商品进行评价打分，部分商品被人们认为其正常工作是理所当然的事情，因此它们收到的评价更多的是无法工作时的差评。正因为有这些情况的出现，我们的数据就不能称为为是随机缺失的，而是非随机缺失(NMAR)。当MAR假设不正确时，我们的推断会有偏差，预测性能也会受到影响。因此，本文提出了一种用于协同过滤的概率矩阵分解模型，该模型从非随机缺失数据中学习，在本文中分别对数据生成过程和数据缺失机制建模，联合学习两个模型。

算法步骤

首先，我们有一个评分矩阵R，形状为n*d，其中\(r_{i,j}\)表示用户i给物品j的评分，R={\(R^{O} , R^{¬O}\)}，\(R^{O} , R^{¬O}\)分别表示观测到的和为观测到的数据。对于每个\(r_{i,j}\)，我们定义了一个二元变量\(x_{i,j}\)，当\(x_{i,j}\)为1时\(r_{i,j}\)可被观测到，当\(x_{i,j}\)为0时\(r_{i,j}\)不可被观测到，所有的\(x_{i,j}\)组成矩阵X。我们假设R是由一个参数为\(\Theta\)的完全数据模型(CDM)生成，X是由一个参数为\(\Omega\)缺失数据模型(MDM)生成。两个模型共享一组隐变量Z。联合模型为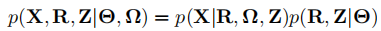
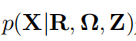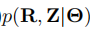其中 为CDM， 为MDM，通常的机器学习模型只关注CDM。

我们现在有一个数据集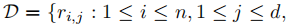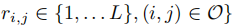，它包含n个用户在d个物品上的评价，可能的评价的值为1<...<L，O是一个(用户,物品)集合,其中用户对物品进行了评价。D是完全评价矩阵R的一个子集，根据D可构建出X，当\(r_{i,j} \in D\)时，\(x_{i,j}\)为1，反之为0。

CDM模型

假设R由两个低秩矩阵\(U \in \mathbb{R} ^{n \times h}\)和\(V \in \mathbb{R} ^{d \times h}\)生成，其中\(h \ll min(n,d)\)。\(r_{i,j}\)由两部分决定，分别是：(1)\(u^{T}_{i}v_{j}\)（原文中是这样写，其实我觉得应该是\(u_{i}v^{T}_{j}\)），其中\(u_{i}\)和\(v_{j}\)分别是U的第i行和V的第j行。(2)L-1个相邻区间，区间边界是\(b_{j,0}<...<b_{j,L}\)，其中\(b_{j,0} = -\infty\)，\(b_{j,L} = \infty\)。引入变量\(a_{i,j} = u^{T}_{i}v_{j} + \epsilon _{i,j}\)，其中\(\epsilon _{i,j}\)为均值为0的高斯噪声，给定\(a_{i,j}\)和\(b_{j}\)的情况下，\(r_{i,j}\)的概率为

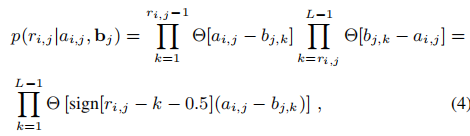
边界B的相关计算如下


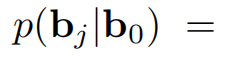
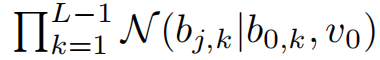
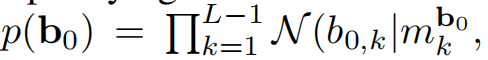
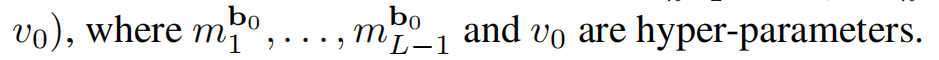
A的相关计算如下，其中\(c_{i,j}=u^{T}_{i}v_{j}\)，\(\gamma _{i}^{row}\)和\(\gamma _{j}^{col}\)分别为R的第i行和第j列噪声。

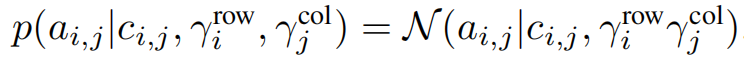
我们对低秩矩阵U和V使用了层次化高斯先验，得到

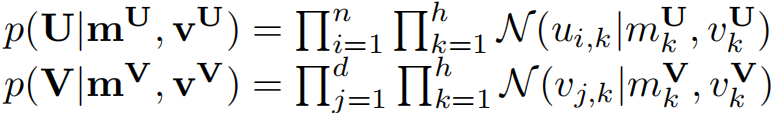
其中\(m^U\)和\(m^V\)是U和V的行平均值，\(v^U\)和\(vv^V\)是U和V的行方差。
另外补充，

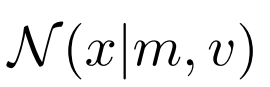
表示均值为m，方差为v的高斯密度。
综上，\(\Theta\)和R的联合概率为

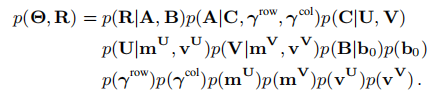
MDM模型

MDM生成一个二元变量矩阵X。我们定义两个低秩矩阵\(E \in \mathbb{R} ^{n \times h}\)和\(F \in \mathbb{R} ^{d \times h}\)。X由E、F、R和一些噪声计算得出。通常情况下，我们假设

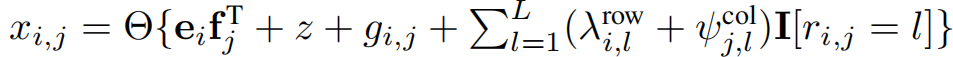
其中\(\Theta \left \{ \cdot \right \}\)是Heaviside阶跃函数，z是偏置，\(g_{i,j}\)是独立同分布的噪声。参数\(\lambda _{i,l}^{row},\varphi _{j,l}^{col}\)决定了\(r_{i,j}\)的值对是否观测到\(r_{i,j}\)的影响。由此得出

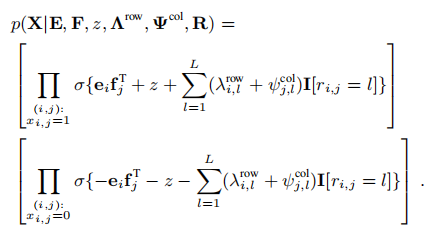
在给定R的情况下，X和\(\Omega\)的联合概率为

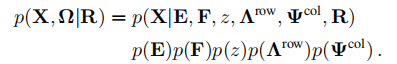
联合模型

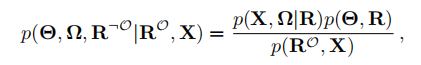
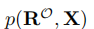为归一化因子。

近似计算

由于上述后验概率难以计算，使用期望传播(EP)和变分贝叶斯(VB)进行近似计算，我们假设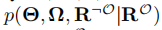为

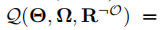
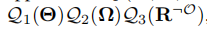
其中，


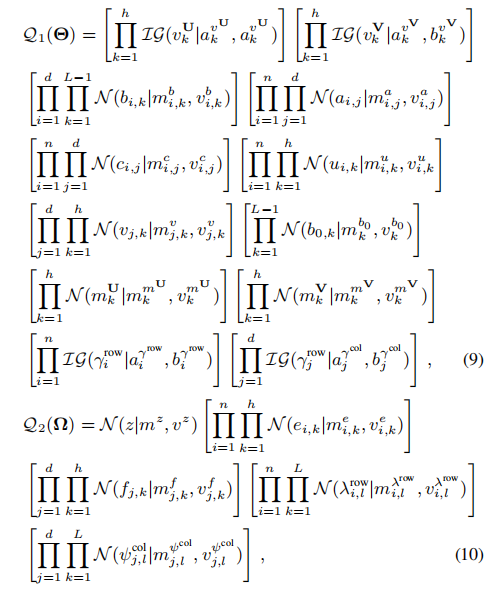
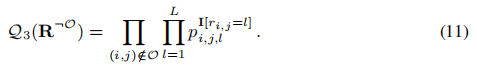
算法流程为

预测

我们可以使用\(\tilde{p}_{i,j,l}^{JM}(x_{i,j})\)计算R中第i行第j列取值为l的概率，当\(x_{i,j}\)为0时，假设这项缺失。当\(x_{i,j}\)为1时，该项应该被观测到，但是它的值是未知的。\(\tilde{p}_{i,j,l}^{JM}(x_{i,j})\)的估计为

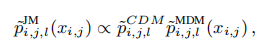
\(\tilde{p}_{i,j,l}^{CDM}\)和\(\tilde{p}_{i,j,l}^{MDM}(x_{i,j})\)分别是CDM和MDM使用近似后验Q生成的预测值。

总结

本篇文章核心思想就是考虑到数据不是随机缺失的，并为之建立起CDM和MDM，这两个模型分别用来生成完整的数据和生成数据缺失的模式，并且联立学习这两个模型，最终进行预测。论文中涉及到大量数学公式，对我来说难度有点大，读了两遍还有些地方不明白，因为这篇论文还有附加材料，可能要读完附加材料才能完全理解。总体感觉这篇论文有很多细节的地方没有讲的很清楚，讲的只是一个大概的思想，可能论文+附加材料才算是真正完整的论文，但是内容实在是太多了，而且难度较大，目前我还很难去读懂。