FISM-Factored Item Similarity Models for Top-N Recommender Systems阅读笔记

动机

本篇论文是在13年KDD上发表的一篇关于Top-N推荐系统的一篇论文。因为在Top-N推荐中，随着数据集矩阵的稀疏性增大，Top-N推荐系统的有效性会随之降低。为了缓解这个问题，本论文提出了一种将item-item相似性矩阵分解为两个低秩潜因素矩阵的乘积的方法。在实验中表明，本论文提出的方法可以有效地处理稀疏数据集矩阵，并且随着矩阵稀疏性增大，本模型的相对与其他模型的性能在不断增大。

符号定义

粗体小写字母表示向量，例如p,q。粗体大写字母表示矩阵，例如R,W。矩阵A的第i行表示为\(a_{i}\)，书法字体表示集合。预测值加^，例如\(\hat{a}\)，估计值加~，例如\(\tilde{a}\)。C和D分别表示用户和物品集合，|C|和|D|分别表示集合大小n,m。在R中，\(r_{ui}\)表示用户对物品的反馈，如果有反馈则为1，否则为0。

与当时较为流行的模型对比

SLIM通过学习一种类似与item-item相似矩阵的聚合系数矩阵，但是它只能找出被一些共同用户购买或评价的物品之间的关系，它不能捕捉到物品之间关系的传递性。NSVD通过将item-item相似矩阵分解成两个低秩矩阵的积,P和Q,\(P\in R^{m\times k}\)，\(Q\in R^{m\times k}\)。FISM与SLIM不同之处在于，FISM求的是item-item相似性矩阵的分解，而SLIM直接求的是这个相似矩阵，相同的是它们在评估\(r_{ui}\)时，都不适用已知的评级信息\(r_{ui}\)。FISM与NSVD相同之处在于它们都是将item-item相似性矩阵分解为两个低秩矩阵，不同之处在于FISM是解决Top-N问题，NSVD解决的是评级问题，FISM不用已知的\(r_{ui}\)评估\(r_{ui}\)，而NSVD使用，这可能导致NSVD中一个项目去推荐自己，此外两种模型估计矩阵的方法也不同。

FISM算法

作者定义了两种FISM的损失函数。

FISMrmse

首先定义损失函数

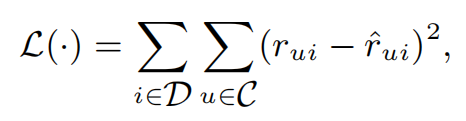
其中\(r_{ui}\)是真实标注值，\(\hat{r}_{ui}\)是估计值。\(\hat{r}_{ui}\)计算公式如下

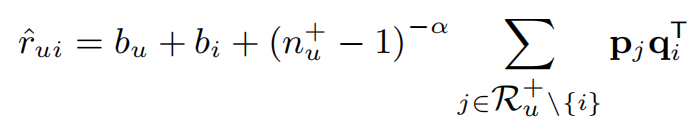
其中\(R_{u}^{+} \setminus \left \{ i \right \}\)代表用户u评价过的物品的集合，集合中不包括物品i。\(p_{j}\)和\(q_{i}\)来自于分解后的低秩矩阵P和Q，\(n_{u}^{+}\)是用户u评价过的物品数，α是一个超参数，用来控制一个物品得到较高的排名需要和多少邻近物品相似，\(b_{u}\)和\(b_{i}\)是用户u和物品i的偏置。在此损失函数下，目标是求出使以下式子最小化的P和Q

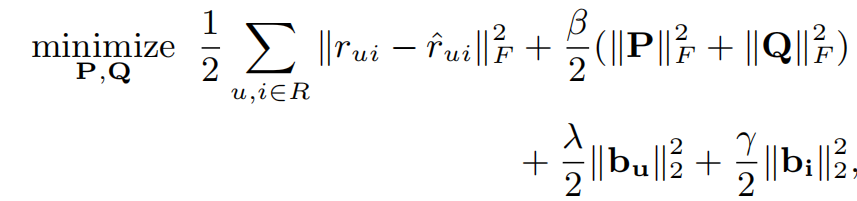
在该损失函数中，使用了所有的用户和所有的物品的组合计算损失，为了减少计算量，每一轮更新可以使用所有\(r_{ui}\)为1的组合和随机抽出\(\rho \cdot nnz\left ( R \right )\)个为0的组合，其中\(\rho\)一般取3~15，nnz(R)是R中不为0的条目数。
整个算法伪代码如下

FISMauc

这个损失函数主要是针对排名的损失函数，定义如下

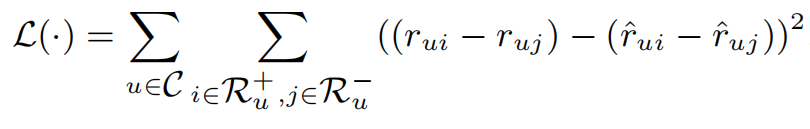
其他定义与FISMrmse相似，在此损失函数下，目标是求出使以下式子最小化的P和Q

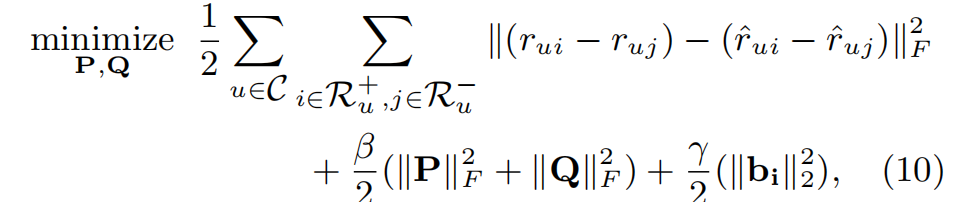
整个算法伪代码如下

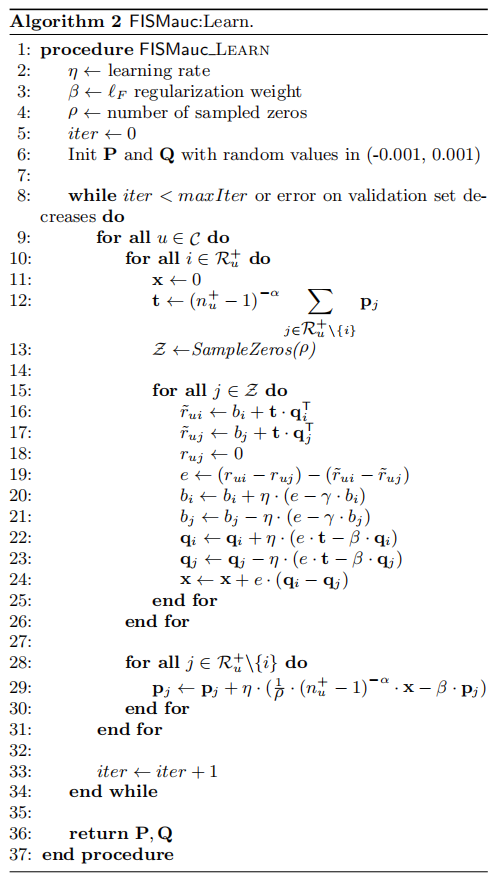
实验部分

定义评估函数HR为

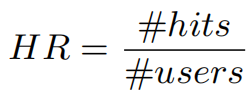
其中#users为总的测试用户数，#hits为测试用户对应的物品在大小为N的推荐列表中的用户数。
评估函数ARHR如下，此函数考虑了测试项目在推荐列表中的位置，相当于加入权重的HR

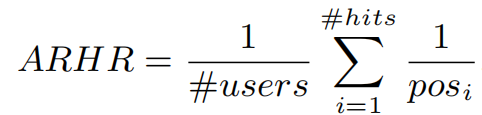
下面是模型参数对结果的影响，偏置部分b对结果总体影响较大，其中item的偏置影响最大；在本次使用的数据集中（ML-100k，Netflix和Yahoo），超参数取值为0.4-0.5之间有较好的结果；如果强制将原矩阵的元素都设置为非负的，效果并没有增强，反而降低；低秩矩阵的维度k越大，通常有越好的效果；矩阵稀疏度在0.1-0.15时，既能保证计算速度够快，同时模型的效果减少很小。另外有一个比较奇怪的现象，在实验结果中，使用FISMrmse损失函数的模型比使用FISMauc的模型效果更好，理论上来讲应该FISMauc效果更好，因为FISMauc是针对排名的损失函数，而Top-N推荐依据就是排名，在当时论文中作者也没有解决这个问题。
另外，我实现了FISMrmse中的关键代码，因为跑这个实验需要的时间有点长，所以我没有完整跑下来。

view code

for _ in range(100):
    zero_idx_pick = zero_idx[np.random.choice(zero_idx.shape[0], pick, replace=False)]
    new_idx = np.concatenate((one_idx, zero_idx_pick), axis=0)
    np.random.shuffle(new_idx)
    for u, i in new_idx:
        nu = 0
        pj = np.zeros_like(P[0][1:], dtype=np.float32)
        for j in range(R[u].shape[0]):
            if R[u][j] == 1 and j != i:
                nu += 1
                pj += P[j,1:]
        x = nu ** (-alpha) * pj
        r_ui = Bu[u] + Bi[i] + Q[i,1:].T @ x
        eui = R[u][i] - r_ui
        Bu[u] = Bu[u] + lr * (eui - Lambda * Bu[u])
        Bi[i] = Bi[i] + lr * (eui - Gamma * Bi[i])
        Q[i, 1:] = Q[i, 1:] + lr * (eui * x - Beta * Q[i,1:])
        for j in range(R[u].shape[0]):
            if R[u][j] == 1 and j != i:
                P[j,1:] = P[j,1:] + lr * (eui * nu ** (-alpha) * Q[i,1:] - Beta * P[j,1:])

总结

本论文核心就是解决item-item相似矩阵稀疏化的问题，解决方法是将该相似矩阵分解为两个低秩矩阵的乘积，这个方法借鉴了SLIM和NSVD这两种方法的思想。该方法在当时的模型中效果是最好的，尤其随着矩阵的稀疏性增大，该模型相对与其他模型的效果会更好。