BPR: Bayesian Personalized Ranking from Implicit Feedback论文笔记

1.动机

本篇论文是2009年有关隐反馈个性化推荐系统的一篇论文，在当时已经有较为先进的方法从隐式反馈的场景为用户推荐商品，如矩阵分解和K近邻方法，但是这些方法没有直接针对排名进行优化。本文中提出了一种用于个性化排名的通用优化标准BPR-Opt，它来源于本问题贝叶斯分析的最大后验概率。

2.一些符号定义及预处理

U表示用户集合，I表示物品集合，隐反馈集\(S \subseteq U\times I\)，隐反馈集形式如下图。

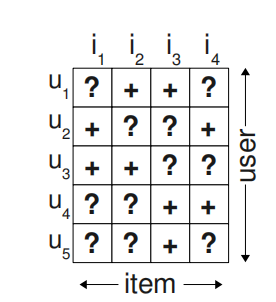
\(> _{u}\)表示用户的偏好，\(i > _{u} j\)表示在有物品i和j的情况下，用户选择i。\(> _{u}\)满足完整性、反对称性和传递性。

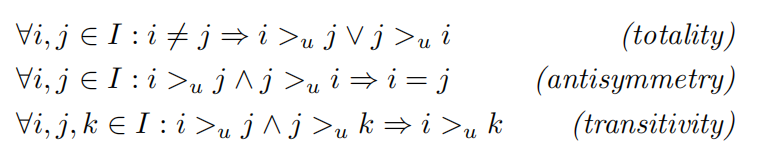
另外定义：

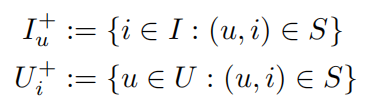
在本论文中需要先把隐反馈集处理成一个个三元组：

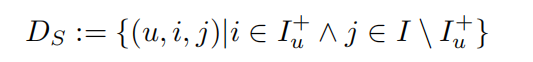
其中\(D_{s}\subseteq U\times I \times I\)，原隐反馈集转换成以下格式

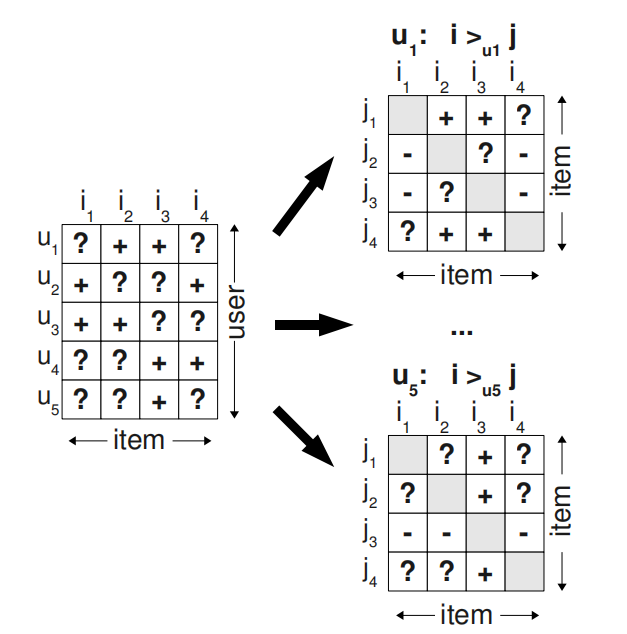
(u,i,j)表示用户u在物品i和j之间更偏好i。

3.BPR算法

BPR基本思想就是最大化后验概率确定所有\(i\in I\)的排名，贝叶斯公式为

其中\(\Theta\)为模型参数。
在这里有两个假设，一是假设用户偏好是独立的，不受其他用户影响，二是假设用户对于每组物品(i,j)偏好也是独立的，不受其它物品影响。

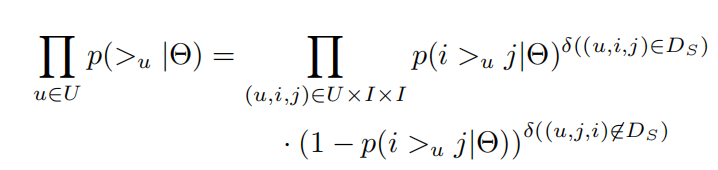
其中\(\delta\)为

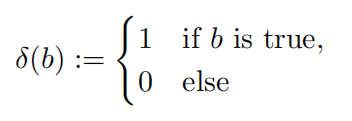
由完整性和反对称性可将上式简化为

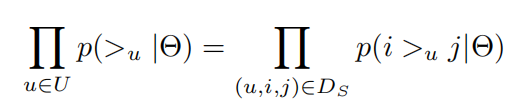
对于\(p\left ( i > _{u} j | \theta \right )\)

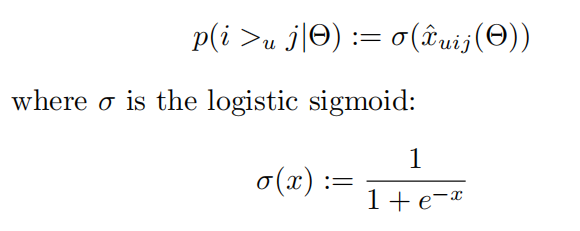
接下来引入先验密度函数\(p\left ( \Theta \right )\)，θ是未知的，这里为了方便计算，假设它服从均值为0，方差为\(\Sigma _{\Theta }\)的正态分布

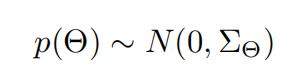
为了减少未知超参数的数量，这里设置

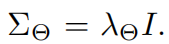
至此，我们就得到了需要最大化的式子

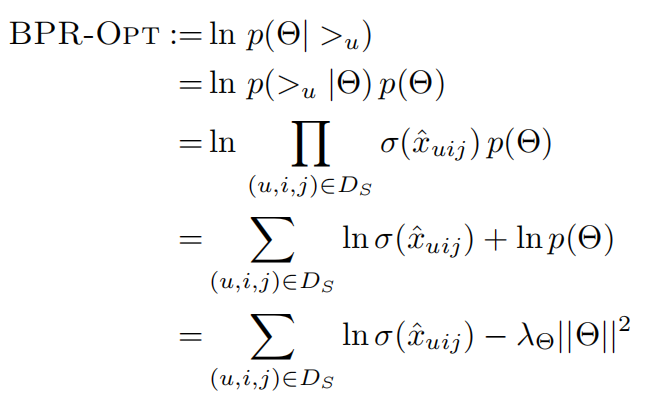
其中\(\lambda _{\Theta }\)是模型特定的正则化参数。

下面一部分我的理解和论文有些出入，最大化上述式子应该是使用梯度上升的方法，论文中这里说的是gradient descent（梯度下降），这里我认为求解一个式子最大值应该是用梯度上升，如果求解的是最小值应当用梯度下降，不过这两个方法可以互相转换，只需要在式子前加一个负号就可以，另外原论文中的求偏导最后一行应该是有误的，多了一个负号。

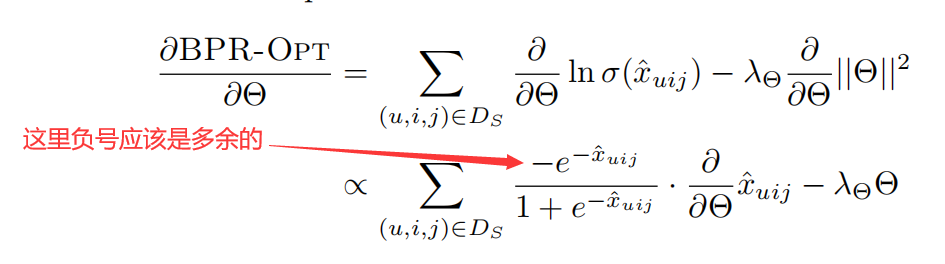
算法步骤如下，使用随机梯度下降的方法，即每次随机抽取一个样本进行参数更新。

4.应用在矩阵分解中

在矩阵分解方法中首先将矩阵\(X:U\times I\)分解为两个低秩矩阵相乘

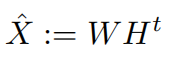
其中\(W:|U| \times k\)，\(H:|I|\times k\)，k是近似矩阵的维度。
\(\hat{x} _{uij}\)计算公式为

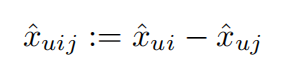
其中\(\hat{x} _{ui}\)为

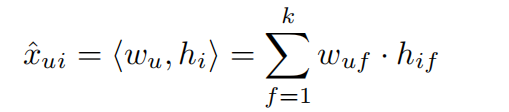
\(\hat{x} _{uij}\)对Θ求导

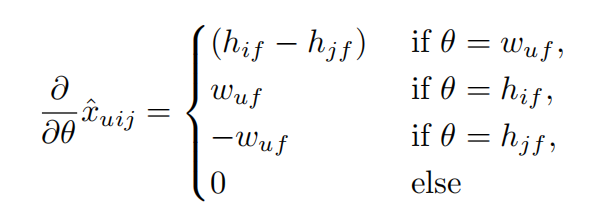
综上，模型的参数更新公式为

\[w_{uf}=w_{uf}+\alpha \left ( \frac{1}{1+e^{\hat{x} _{uij}}}\left ( h_{if}-h_{jf} \right ) +\lambda w_{uf} \right ) \]

\[h_{if}=h_{if}+\alpha \left ( \frac{1}{1+e^{\hat{x} _{uij}}} w_{uf} +\lambda h_{if} \right ) \]

\[h_{jf}=h_{jf}+\alpha \left ( \frac{1}{1+e^{\hat{x} _{uij}}} \left ( -w_{uf} \right ) +\lambda h_{jf} \right ) \]

5.应用在k近邻算法中

k近邻算法依赖于计算物品或用户之间的相似度，对于用户u和物品i的预测取决于物品i与用户u过去喜欢的其他k个物品的相似度，\(x_{ui}\)计算公式为

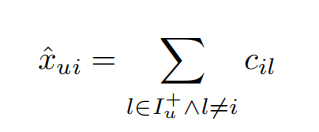
其中\(C: I \times I\)是物品相似度矩阵，因此模型的参数就是C。
\(\hat{x} _{uij}\)的梯度为

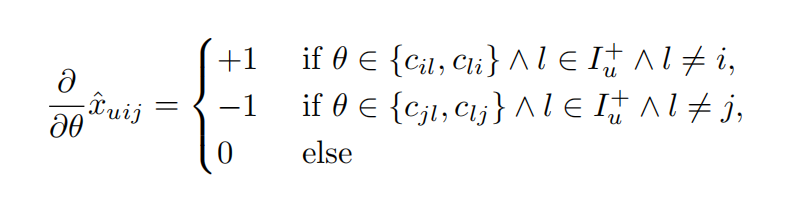
参数更新公式为

\[c_{il}=c_{il}+\alpha \left ( \frac{1}{1+e^{\hat{x} _{uij}}} +\lambda c_{il} \right ) \]

\[c_{jl}=c_{jl}+\alpha \left ( \frac{-1}{1+e^{\hat{x} _{uij}}} +\lambda c_{jl} \right ) \]