20172324 2018-2019-1 《程序设计与数据结构》第九周学习总结
20172324 2018-2019-1 《程序设计与数据结构》第九周学习总结
教材学习内容总结
无向图
- 无向图是一种边为无序结点对的图:
-
图由顶点和边组成
-
顶点由名字或标号来表示,如:A、B、C、D;
边由连接的定点对来表示,如:(A,B),(C,D),表示两顶点之间有一条边。 -
如果图中的两个顶点之间有边连接,则称它们是邻接的
-
A和B邻接(两个顶点之间有边连接),而A和D不邻接。边(A,A)表示的是连接A到自身的一个环(自循环)。
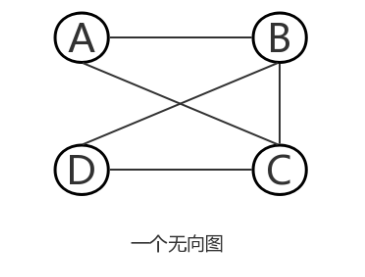
-
完全图:含有最多条边的无向图:
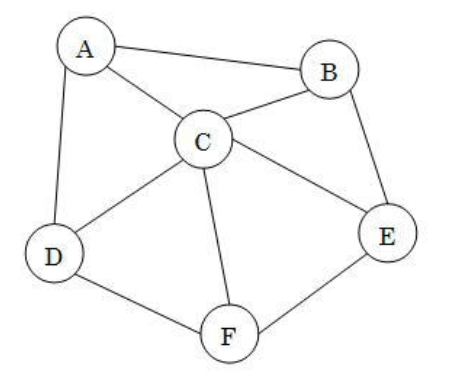
-
要使该图是完全的,要求有n(n-1)/2条边,当然,这里假设其中没有边是循环的
- 路径:连接图中两个顶点的边的序列,可以由多条边组成。 是图中连接两个顶点的边的序列
- 路径长度:路径中所含边的数目(或者是顶点个数减1)
- 连通的:无向图中任意两个顶点间都有路径,书上p313给的简单解法:在一个含有n个顶点的图中,当且仅当对每个顶点v,从v开始的广度优先遍历的resultList大小都是n,则改图就是连通的。
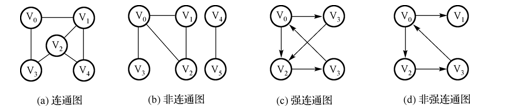
完全图一定是连通图,连通图不一定是完全图
-
环路:首顶点与末顶点相同且没有重复边的路径
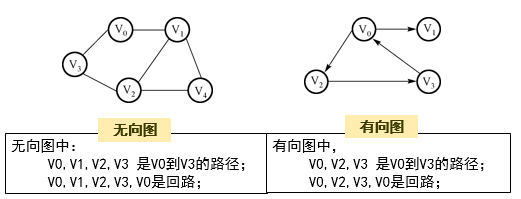
-
无环图是没有环的图。无向树是一种连通的无环无向图,其中一个元素被指定为树根。
有向图
-
有向图:也称双向图。顶点之间有序连接,边是顶点的有序对。也就是边(A,B)和(B,A)方向不同。
-
注意联通有向图与无向图不同,有向边决定连通性。例如:
左图为联通图,右图不联通,因为从任何顶点到顶点1都没有路径。
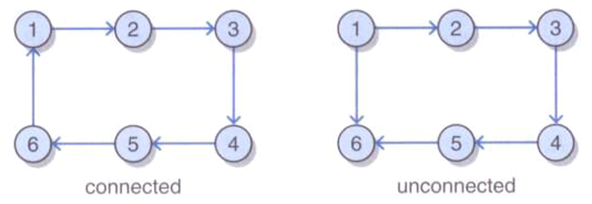
-
拓扑序:有向图中没有环路,且有一条从A到B的边,则可以吧顶点A安排在顶点B之前,这种排列得到的顶点次序称为拓扑序。
-
树也是图,且有如下属性:
- 不存在其他顶点到树根的连接。
- 每个非树根元素恰好有一个连接。
- 树根到每个其他顶点都有一条路径。
网络
- 也称作加权图,每条边都对应一个权值(数据信息)的图
- 可以是无向的也可以是有向的
- 对于网络,用一个三元组来表示每条边:由起始顶点、终止顶点和权重构成。

常用的图算法
- 遍历:
- 广度优先遍历:从一个顶点开始,辐射状地优先遍历其周围较广的区域。类似于树的层序遍历
- 深度优先遍历:图的深度优先搜索,类似于树的先序遍历,所遵循的搜索策略是尽可能“深”地搜索图。
- 深度优先遍历与广度优先遍历的唯一不同是,使用的是栈而不是队列来管理遍历。
- 测试连通性:
- 最小生成树:所含边权值之和小于其他生成树的边的权值之和。
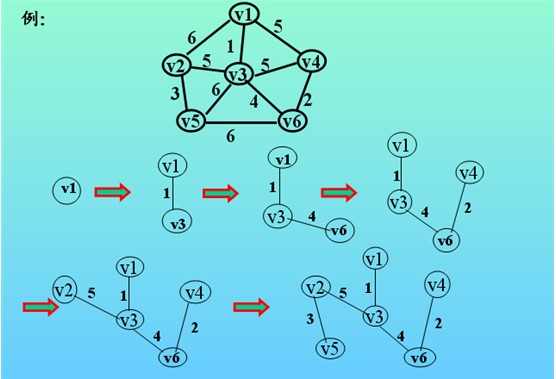
- 判定最短路径:(1)判定起始顶点和目标顶点之间是否存在最短路径(两个顶点之间边数最少的路径)。(2)在带权图中找到最短路径。
- 最小生成树:所含边权值之和小于其他生成树的边的权值之和。
图的实现策略
- 邻接列表:详情参考这个博客图的存储结构之邻接列表

以图a所示的无向图为例,只需将如图b所示的邻接矩阵,逐行地转换为图c所示的一组列表,即可分别记录各顶点的关联边(或等价地,邻接顶点)。这些表便称之为邻接表(adjacency list)。
以上图为例,对于图a的四个顶点A,B,C,D四个顶点的属性上添加一个对于弧的指针,指向以该顶点为起点的一条弧(被称为该顶点为起点的所有弧的首弧)。而对于弧的属性也增加一个对顶点的指针和对弧的指针,其中对于顶点的指针指向该弧的终点(弧头),而对弧的指针指向已该弧的起点(弧尾)的另一条弧。
这样,根据一个顶点的弧的指针,通过这个弧对于其他的弧的指针即可定义出该顶点作为起点(弧尾)的所有弧。也可以根据一个顶点的弧的指针,通过这个弧对于弧的终点的指针(弧头)便可定义出由该顶点起的一条路。
- 邻接矩阵:详情参考这个博客图的邻接矩阵的实现
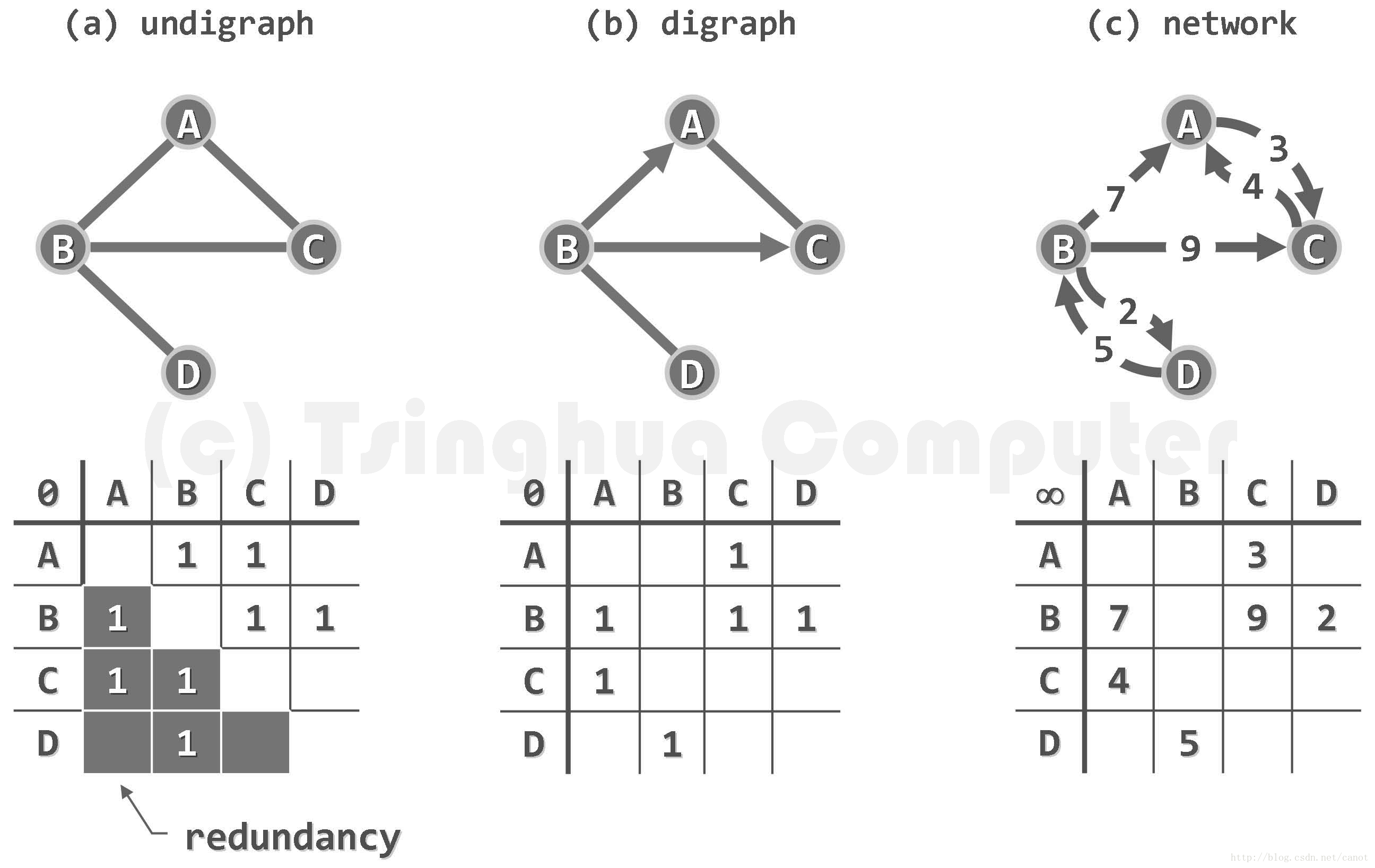
邻接矩阵(adjacency matrix)是图ADT最基本的实现方式,使用二维数组A[n][n]来表示由n个顶点构成的图。二维数组中的A[i][j]表示一条从来顶点i为起点到顶点j的弧。对于无权图,存在(不存在)从顶点u到v的边,当且仅当A[u][v] =1(0)。上图a,b即为无向图和有向图的邻接矩阵实例。图c所示,矩阵各单元可从布尔型改为整型或浮点型,记录所对应边的权重。对于不存在的边,通常统一取值null。
教材学习中的问题和解决过程
-
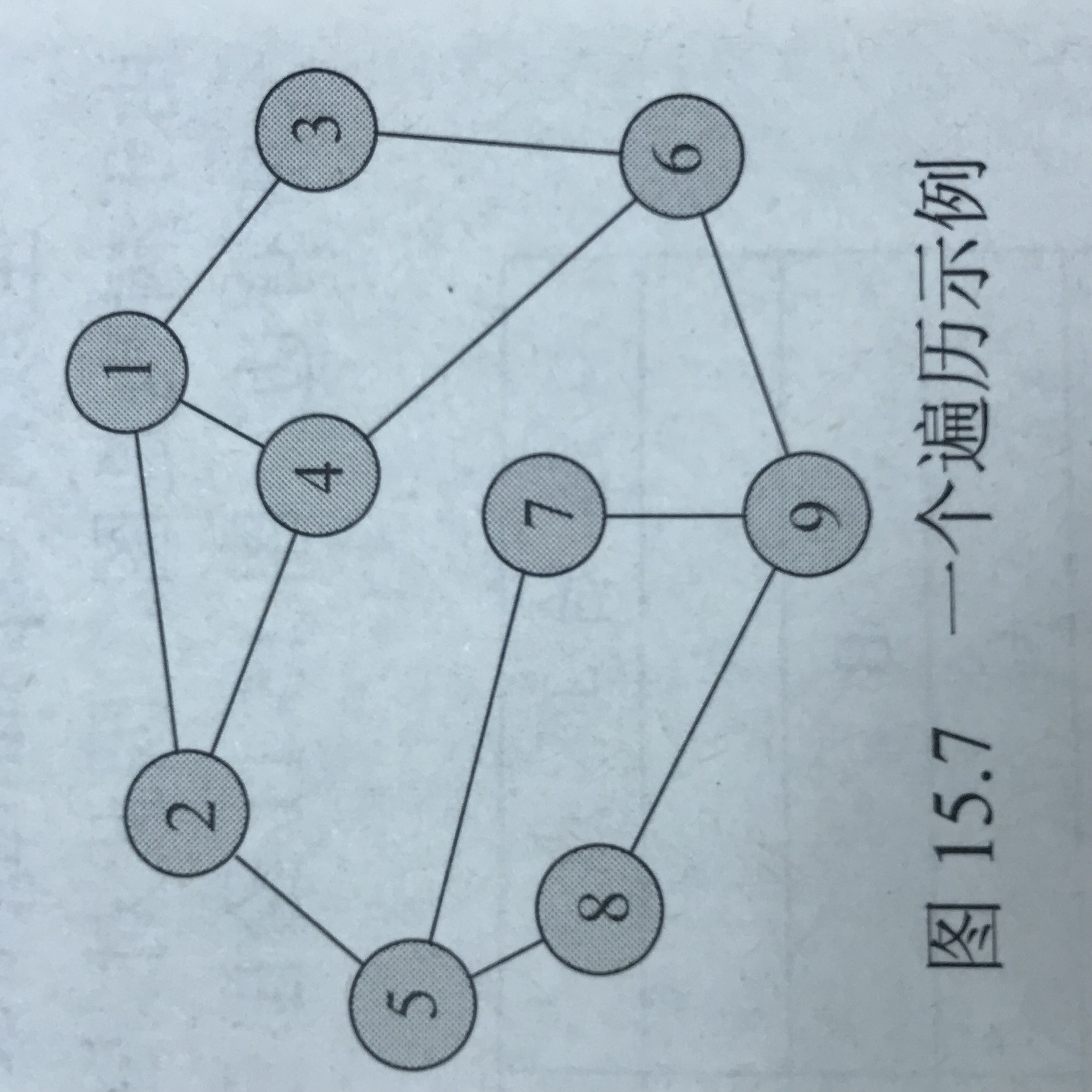
问题1:如何进行广度优先遍历,书上给了一个例子,但是只看书有一点不能理解,特别是312-313的代码和汉字
-
问题1解决方案:我就将书上比较正式的文字转化成了口水文字写在旁边了,然后在图上画了一下大概和层序遍历差不多的顺序,不怎么会做图,所以就用照片代替了


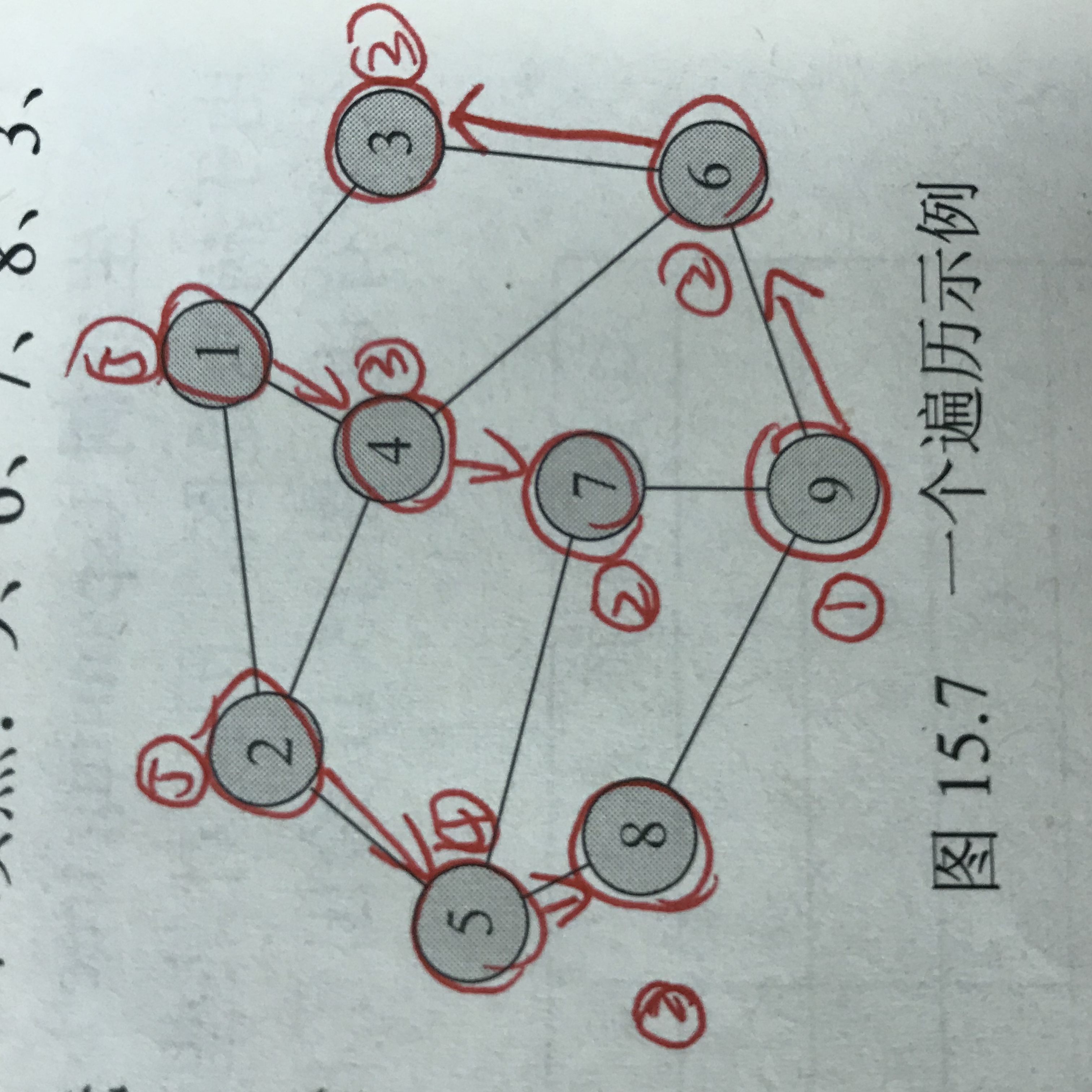
最后通过广度优先遍历的序列是:9、6、7、8、3、4、5、1、2
- 问题2:如何进行深度优先遍历,书上也没说
- 问题2解决方案:在网山找到一个图文并茂又简答易懂的博客,引用一下:
现在我们从1号顶点开始遍历这个图(遍历指的是把每一个顶点都访问一次)。使用深度优先搜索来遍历这个图我们将得到以下结果:
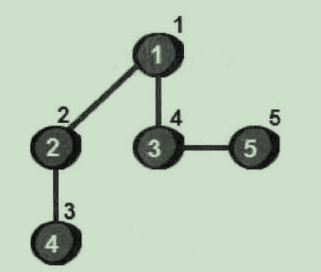
使用深度优先搜索来遍历这个图的具体过程是:
首先从一个未走到过的顶点作为起始顶点,比如1号顶点作为起点。
沿1号顶点的边去尝试访问其它未走到过的顶点,首先发现2号顶点还没有走到过,于是来到了2号顶点。
再以2号顶点作为出发点继续尝试访问其它未走到过的顶点,这样又来到了4号顶点。
再以4号顶点作为出发点继续尝试访问其它未走到过的顶点。
但是,此时沿4号顶点的边,已经不能访问到其它未走到过的顶点了,所以需要返回到2号顶点。
返回到2号顶点后,发现沿2号顶点的边也不能再访问到其它未走到过的顶点。此时又会来到3号顶点(2->1->3),再以3号顶点作为出发点继续访问其它未走到过的顶点,于是又来到了5号顶点。
至此,所有顶点我们都走到过了,遍历结束。
深度优先遍历的主要思想是:
首先以一个未被访问过的顶点作为起始顶点,沿当前顶点的边走到未访问过的顶点;
当没有未访问过的顶点时,则回到上一个顶点,继续试探别的顶点,直到所有的顶点都被访问过。
在此我想用一句话来形容 “一路走到头,不撞墙不回头”。
代码调试中的问题和解决过程
- 问题一:在做pp15.1为什么无向图的边会出现输入错误,抛出的异常
Exception in thread "main" java.lang.:4
- 问题一解决方案:开始的时候无法解决,问了半天也不知道怎么办。后来调试之后我发现是我的输入格式出了问题,因为我用的是scan.next(),这个输入的时候只要加上空格就不会有问题 没有空格就有问题了....以后有问题 先加空格
代码托管
上周考试错题总结
A minheap stores its largest element at the root of the binary tree, and both children of the root of a minheap are also minheaps.
A .True
B .Flase(正确答案)
小顶堆根结点的键值是所有堆结点键值中最小者。
To maintain the completeness of the tree, there is only one valid element to replace the root, and that is the element stored in the first leaf in the tree.
A .True
B .Flase(正确答案)
为了保持树的完整性,需要一个元素来替代根的元素,是根的元素不是第一个叶子中的元素
结对及互评
正确使用Markdown语法(加1分)
模板中的要素齐全(加1分)
教材学习中的问题和解决过程, (加3分)
代码调试中的问题和解决过程, 无问题
感想,体会真切的(加1分)
点评认真,能指出博客和代码中的问题的(加1分)
- 结对同学学号21
基于评分标准,我给以上博客打分:8分。
点评过的同学博客和代码
-
本周结对学习情况
- 教材第15章,运行教材上的代码
内容详略得当;
代码调试环节比较详细
- 教材第15章,运行教材上的代码
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0 | 1/1 | 20/20 | |
| 第二周 | 300/500 | 1/2 | 18/38 | |
| 第三周 | 300/600 | 1/3 | 18/38 | |
| 第四周 | 400/1000 | 2/5 | 18/38 | |
| 第五周 | 300/1300 | 1/6 | 18/38 | |
| 第六周 | 300/1300 | 3/9 | 18/38 | |
| 第七周 | 300/1300 | 3/9 | 18/38 | |
| 第八周 | 300/1600 | 2/11 | 18/38 | |
| 第九周 | 300/1900 | 1/12 | 18/38 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号