20172324 2018-2019-1 《程序设计与数据结构》第八周学习总结
20172324 2018-2019-1 《程序设计与数据结构》第八周学习总结
教材学习内容总结
堆
- 具有两个附加属性的二叉树:
- 是一颗完全树
- 对每一结点,它小于或等于其左孩子和右孩子(最小堆)
- 最大堆的结点大于或等于它的左右孩子
- 最小堆将其最小元素存储在该二叉树的根处,其根的两个孩子同样也是最小堆
| 操作 | 说明 |
|---|---|
| addElement | 将给定元素添加到该堆中 |
| removeMin | 删除堆的最小元素 |
| findMin | 返回一个指向堆中的最小元素的引用 |
-
addElement操作
- 要求插入元素是可比较的
- 维持该堆的完全性属性和有序属性,插入的元素位置只存在一个正确的位置,要不然在h层左边的下一个空位置,要不然在h+1层左边的第一个位置。
- 添加之后进行排序(过程名叫筛选)
- 在堆实现中,会对最末一片叶子进行跟踪记录。
-
removeMin操作
- 对于最小堆来说,Min就是根的位置的元素
- 维持该堆的完全性,能替换根的合法元素只有一个就是最末一片叶子上存储的元素。
- 删除之后进行排序(过程名叫筛选)
-
findMin操作:
- 最小堆中的最小元素存储在根中,所以只需要返回存储在根中的元素。
使用堆:优先级队列
- 两个规则:
- 具有更高优先级的项排在前面。(不是FIFO)
- 具有相同优先级的项按先进先出的规则排列。(FIFO)
- 解决方案:
- 使用队列列表
- 使用最小堆。
//要先解决对相同优先级的进行先进先出的排序
//创建一个PriorityQueueNode对象,存储将被放置在队列中的元素,该元素的优先级,以及元素放进队列的顺序
public PrioritizedObject(T element, int priority)
{
this.element = element;//元素
this.priority = priority;//优先级
arrivalOrder = nextOrder;//放入队列的顺序
nextOrder++;
}
//再解决优先级相同时的比较
//为PriorityQueueNode类定义一个CompareTo方法,来完成优先级相同时的比较
public int compareTo(PrioritizedObject obj)
{
int result;
if (priority > obj.getPriority())
result = 1;
else if (priority < obj.getPriority())
result = -1;
else if (arrivalOrder > obj.getArrivalOrder())
result = 1;
else
result = -1;
return result;
}
堆的实现
-
用链表实现堆:堆是二叉树的一种扩展,所以在插入元素后仍旧能够向上遍历该树,所以堆中的结点必须存储指向其双亲的指针。
-
用数组实现堆:首先检查可用空间,如有需要进行扩容。
-
链表实现和数组实现的addElement操作的时间复杂度同为O(log n)
-
链表实现和数组实现的removeMin操作的复杂度同为O(log n)
-
findMin操作只需要返回一个引用,因此复杂度为O(1)
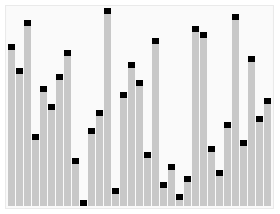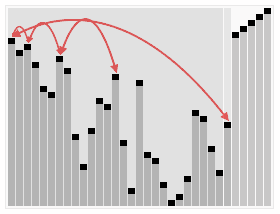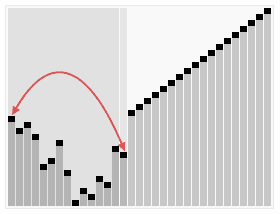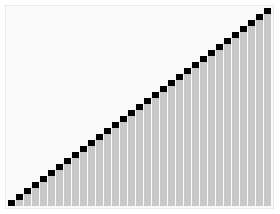
堆排序
- 最小堆排序结果为升序排序,最大堆排序结果为降序排序。
- 复杂度为O(n log n)
- heapSort方法将一组元素一项项地插入到堆中,然后一次删除一个。因为最大元素最先从堆中删除,所以一次次删除得到的元素将是有序序列,而且是降序的。同理,一个最小堆可用来得到升序的排序结果。
教材学习中的问题和解决过程
-
问题1:对于堆排序的详细步骤(具体顺序)不清楚,教材上也只提供了思路。
-
问题1解决方案:
构造初始堆,以小顶堆为例,给无序序列构造一个大顶堆,就像下面这棵树一样,但这个例子要求先删除最小的再插入:
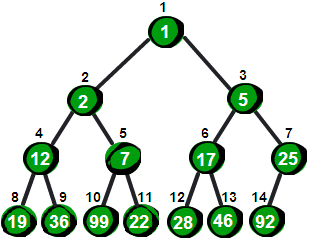
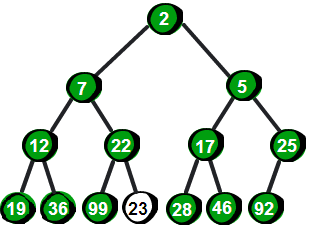
首先我们先把这个14个数按照最小堆的要求(就是所有父结点都比子结点要小)放入一棵完全二叉树,就像下面这棵树一样。
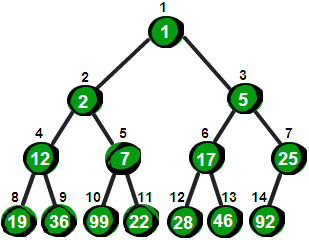
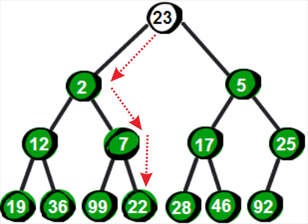
很显然最小的数就在堆顶,假设存储这个堆的数组叫做h的话,最小数就是h[ 1]。接下来,我们将堆顶的数删除,并将新增加的数23放到堆顶。显然加了新数后已经不符合最小堆的特性,我们需要将新增加的数调整到合适的位置。那如何调整呢?

向下调整!我们需要将这个数与它的两个儿子2和5比较,并选择较小一个与它交换,交换之后如下。
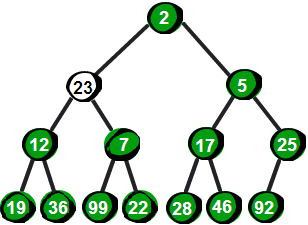
我们发现此时还是不符合最小堆的特性,因此还需要继续向下调整。于是继续将23与它的两个儿子12和7比较,并选择较小一个交换,交换之后如下。
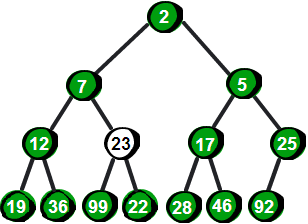
到此,还是不符合最小堆的特性,仍需要继续向下调整直到符合最小堆的特性为止。
我们发现现在已经符合最小堆的特性了。综上所述,当新增加一个数被放置到堆顶时,如果此时不符合最小堆的特性,则将需要将这个数向下调整,直到找到合适的位置为止,使其重新符合最小堆的特性。
-
问题2:对书上getNextParentAdd代码的理解
-
问题2解决方案:和刘辰一讨论,发现我俩在这个问题上出现的疑惑是一样的,在这里要分三种情况讨论,当是一颗平衡二叉树时,lastnode的父节点是根结点的左孩子,往上判断发现父节点没有兄弟节点说明是根节点,那么父节点的右孩子就是下一个父节点了。当是一颗完全二叉树的时候,lastnode的父节点是根节点的右孩子,经历两次循环到lastnode那一层的第一个左孩子,最后进入打的else和while循环,它多了一个左孩子。当不是一颗满二叉树也不是一颗平衡二叉树且lastnode是左孩子的时候,进入if语句父节点为根节点的右孩子,直接return后就变成一颗完全二叉树了。
private HeapNode<T> getNextParentAdd() {
HeapNode<T> result = lastNode;
while ((result != root) && (result.getParent().getLeft() != result))
result = result.getParent();
if (result != root)
if (result.getParent().getRight() == null)
result = result.getParent();
else {
result = (HeapNode<T>) result.getParent().getRight();
while (result.getLeft() != null)
result = (HeapNode<T>) result.getLeft();
}
else
while (result.getLeft() != null)
result = (HeapNode<T>) result.getLeft();
return result;
}
具体的图片我就直接把刘辰画的图拿来了
代码调试中的问题和解决过程
-
问题一:heapifyAdd操作的代码
-
问题一解决方案:
思路:找到插入元素的双亲结点进行比较,把插入元素放入temp暂存,如果比双亲结点小(或者大),则把双亲结点向下移(或者不动),直到找到双亲结点不动的情况,则找到该插入元素的位置,把temp给双亲结点的孩子。
private void heapifyAdd()
{
T temp;
int next = count - 1;
temp = tree[next];
while ((next != 0) &&
(((Comparable)temp).compareTo(tree[(next-1)/2]) < 0))
{
tree[next] = tree[(next-1)/2];
next = (next-1)/2;
}
tree[next] = temp;
}
代码托管
上周考试错题总结
What type does "compareTo" return?
A .int
B .String
C .boolean
D .char
compareTo返回的是-1,0,1。所以为int值
结对及互评
正确使用Markdown语法(加1分)
模板中的要素齐全(加1分)
教材学习中的问题和解决过程, (加3分)
代码调试中的问题和解决过程, 无问题
感想,体会真切的(加1分)
点评认真,能指出博客和代码中的问题的(加1分)
- 结对同学学号21
基于评分标准,我给以上博客打分:8分。
点评过的同学博客和代码
-
本周结对学习情况
- 教材第12章,运行教材上的代码
内容详略得当;
代码调试环节比较详细
- 教材第12章,运行教材上的代码
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0 | 1/1 | 20/20 | |
| 第二周 | 300/500 | 1/2 | 18/38 | |
| 第三周 | 300/600 | 1/3 | 18/38 | |
| 第四周 | 400/1000 | 2/5 | 18/38 | |
| 第五周 | 300/1300 | 1/6 | 18/38 | |
| 第六周 | 300/1300 | 3/9 | 18/38 | |
| 第七周 | 300/1300 | 3/9 | 18/38 | |
| 第八周 | 300/1600 | 2/11 | 18/38 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号