20172324 2018-2019-1 《程序设计与数据结构》第六周学习总结

20172324 2018-2019-1 《程序设计与数据结构》第六周学习总结

教材学习内容总结

概述

树由一个包含结点(node)和边(edge)的集构成，其中的元素被存储在这些结点中，边将一个结点和另一个结点连接起来，每一结点都位于该树层次结构中某一特定层上，树的根(root)就是那个位于该树顶层的唯A,B,C,D,E,H

  1. 结点的子树的根称为该结点的孩子，此结点就是孩子的双亲，一个结点只能有一个双亲，但是一个结点可以有多个孩子；
  2. 同一个双亲的孩子称为兄弟；
  3. 根结点是树中唯一一个没有双亲的结点，没有任何孩子的结点称为叶子，至少有一个孩子的非根结点称为一个内部结点
  4. 结点的祖先是从根节点到该结点所经过的所有结点；结点的子孙是以此结点为根的子树的子树的任一结点；双亲在同一层的结点称为堂兄弟
  5. 结点的层次（Level）从根开始定义起，根为第一层，根的孩子为第二层，树中结点的最大层次成为树的深度（Depth）或高度。
  6. 树的度是树内任意节点可以具有的最大孩子数目

【基本术语】

  • 结点的度（Degree）：结点的子树个数；
  • 树的度：树的所有结点中最大的度数；
  • 叶结点（Leaf）：度为0的结点；
  • 父结点（Parent）：有子树的结点是其子树的根节点的父结点；
  • 子结点/孩子结点（Child）：若A结点是B结点的父结点，则称B结点是A结点的子结点；
  • 兄弟结点（Sibling）：具有同一个父结点的各结点彼此是兄弟结点；
  • 路径和路径长度：从结点n1到nk的路径为一个结点序列n1，n2，...，nk。ni是ni+1的父结点。路径所包含边的个数为路径的长度；
  • 祖先结点（Ancestor）：沿树根到某一结点路径上的所有结点都是这个结点的祖先结点；
  • 子孙结点（Descendant）：某一结点的子树中的所有结点是这个结点的子孙；
  • 结点的层次（Level）：规定根结点在1层，其他任一结点的层数是其父结点的层数加1；
  • 树的深度（Depth）：树中所有结点中的最大层次是这棵树的深度；

例题：

上图D是A的孩子，A是D的双亲。H,I,J为互为兄弟。G与E、F、H、I、J互为堂兄弟。M的祖先为A、D、H。K、L、F、G、M、I、J都是树的叶子。A、B、C、D、E、H为非终端结点。A的度为3，C的度为1，F的度为0。树的度为 3 。树的深度为4。

  • 树的分类
    • 按照树中任一结点可以具有的最大孩子数目(二叉树：结点最多具有两个孩子)
    • 按照该树平衡与否(完全树、满树)

实现树的策略

运用链式结构，每一结点定义成TreeNode类，每一结点都包括一个指针，它指向将要存储在该结点的元素，以及该结点所有可能孩子的指针。

  • 树的数组实现之计算策略

一种可能的策略就是将元素n的左孩子置于位置位于(2xn+1)，将右孩子置于(2x(n+1))

  • 树的数组实现之模拟链接策略

每一结点存储的将是每一孩子(甚至还可能是双亲)的数组索引，而不是作为指向其孩子(甚至还可能是双亲)指针的对象引用变量

树的遍历

前序 中 左 右
中序 左 中 右
后序 左 右 中

  • 前序遍历

    若树为空，则空操作返回。否则，先访问根节点，然后前序遍历左子树，再前序遍历右子树。

    • 中序遍历

    若树为空，则空操作返回。否则，从根节点开始（注意并不是先访问根节点），中序遍历根节点的左子树，然后是访问根节点，最后中序遍历根节点的右子树。

    • 后序遍历

    若树为空，则空操作返回。否则，从左到右先叶子后节点的方式遍历访问左右子树，最后访问根节点。

    • 层序遍历

    若树为空，则空操作返回。否则，从树的第一层，也就是根节点开始访问，从上到下逐层遍历，在同一层中，按从左到右的顺序结点逐个访问。

举个例子：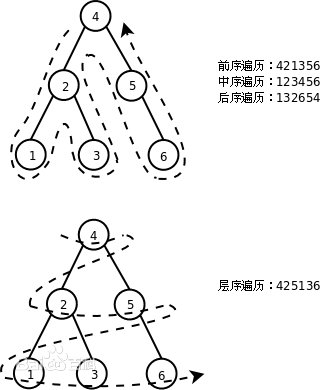

二叉树

public interface BinaryTreeADT<T> {
    public T getRootElement();
    public boolean isEmpty();
    public int size();
    public boolean contains(T targetElement);
    public T find(T targetElement);
    public String toString();
    public Iterator<T> iterator();
    public Iterator<T> iteratorInOrder();
    public Iterator<T> iteratorPreOrder();
    public Iterator<T> iteratorPostOrder();
    public Iterator<T> iteratorLevelOrder();

}

二叉树的性质

（性质一）在二叉树的第 i 层上至多有 2^(i-1)个结点 （i >=1）

第一层 ：1(2^0) 第二层：2(2^1)
第三层：4(2^2) 第四层：8(2^3)

（性质二）深度为 k 的二叉树至多有2^k -1个结点（k>=1）
由性质一得：第k层，2^k - 1 个结点
1+2+22+....+2(k-1) = ( 1 - 2^k)/(1-2) = 2^k - 1

（性质三）★对任何一棵二叉树 T ，如果其终端结点数位n0，度为2的结点数位n2，则n0=n2+1。
式一： n = n0 + n1 + n2 （结点总数 等于 度为0 加 度为1 加 度为2）
式二： n = n0 + 2*n2 +1（n = 分支总数+1 ；分支总数 = n1+n2 （分支是由度为1，度为2的结点射出的））
式二 - 式一得： n0 = n2 + 1

★完全二叉树

一棵深度为 k 且有2^k - 1个结点的二叉树为满二叉树
（性质一）具有n个结点的完全二叉树的深度为 」 log 2 n」+1
由普通的二叉树性质二得：深度为k，结点数最多2^k - 1个，那么log一下就出来了

（性质二）如果对一棵有n个结点的完全二叉树（其深度为」 log 2 n」+1 ）的结点按层序编号（从第一层到最后一层，每层从左到右），对任一结点i（1<= i <=n）有

（1）如果 i =1，则结点 i 是二叉树的根，无双亲；
如果 i >1，则其双亲Parent( i ) 是结点 」i / 2」

（2）如果2xi >n，则结点 i 无左孩子（结点 i 为叶子节点） ；否则其左孩子LChild( i )是结点2*i。

（3）如果2xi+1>n，则结点 i 无右孩子；否则其右孩子RChild( i )是结点2xi+1。

使用二叉树：表达式树

表达式树的根及其内部结点包含着操作，且所有的叶子也包含着操作数，对表达式树的求值是从下往上的。

从一个后缀表达式构建一颗表达式树(书上的例子太复杂了找了简单多的进行理解)：
如同后缀表达式求值一样，我们逐次读取后缀表达式的每一个符号，如果符号是操作数，那么我们就建立一个单节点树并将一个指向它的指针推入栈中；如果符号是操作数，则从栈中弹出两棵树T1和T2（先弹出T1），并形成一颗以操作符为根的树，其中T1为右儿子，T2为左儿子；然后将新的树压入栈中，继续上述过程。

用链表实现二叉树

教材学习中的问题和解决过程

  • 问题1：程序列表10.4与10.5对表达式树的计算太长了有点难以理解...

  • 问题1解决方案：从一个后缀表达式构建一颗表达式树(书上的例子太复杂了找了简单多的进行理解)：
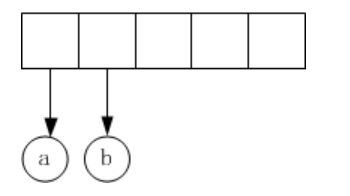
    如同后缀表达式求值一样，我们逐次读取后缀表达式的每一个符号，如果符号是操作数，那么我们就建立一个单节点树并将一个指向它的指针推入栈中；如果符号是操作数，则从栈中弹出两棵树T1和T2（先弹出T1），并形成一颗以操作符为根的树，其中T1为右儿子，T2为左儿子；然后将新的树压入栈中，继续上述过程。如“a b + c d e + * *”生成表达式树的主要过程如下图所示：

    （1）依次读入操作数a 和 b，并压入栈中

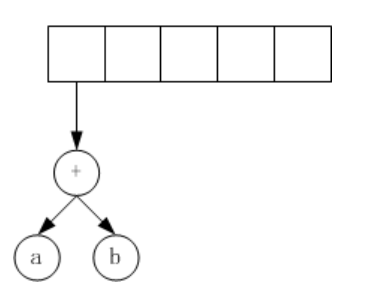
    （2）遇到操作符“+”

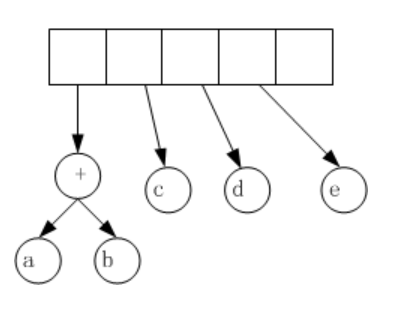
    （3）遇到c d e 操作数

    （4）遇到“+”操作符

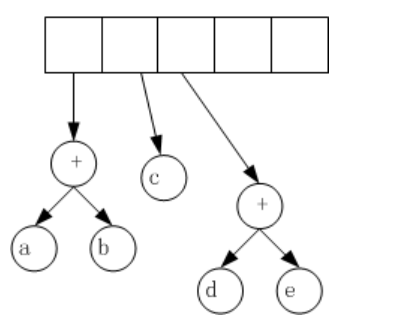
    （5）遇到“*”操作符

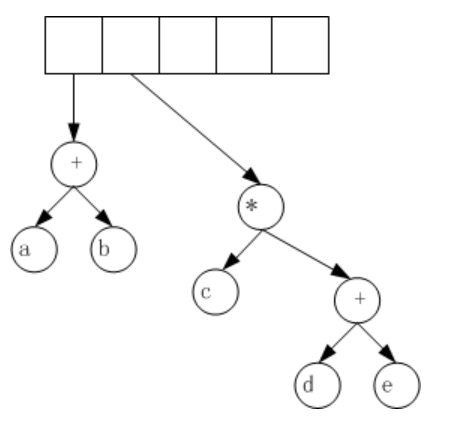
    （6）遇到“*”操作符

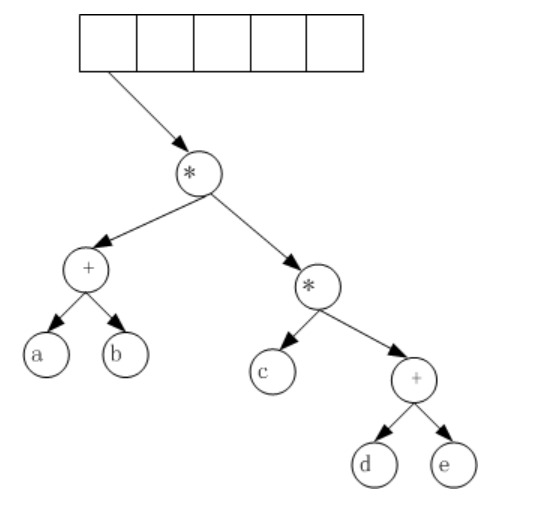
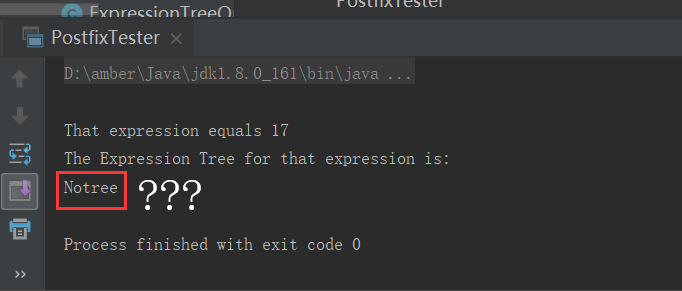
  • 问题2：弄明白了如何使用链表建立二叉树，可是测试书上的代码的时候发现noTree...玩呢

  • 问题2解决方案：首先现在书上找答案，感觉问题应该是出在printTree方法里，打开果然发现直接打印"noTree"的下面注释掉了一句return (treeStack.peek()).printTree();本来我满心欢喜，结果消去注释后再尝试发现只能输出两个操作符，佛了，最后问了同学才知道是因为代码没有完整，书上pp的内容才能将tree输出

代码调试中的问题和解决过程

  • 问题一：我的BackPainAnaylyzer出现问题如下

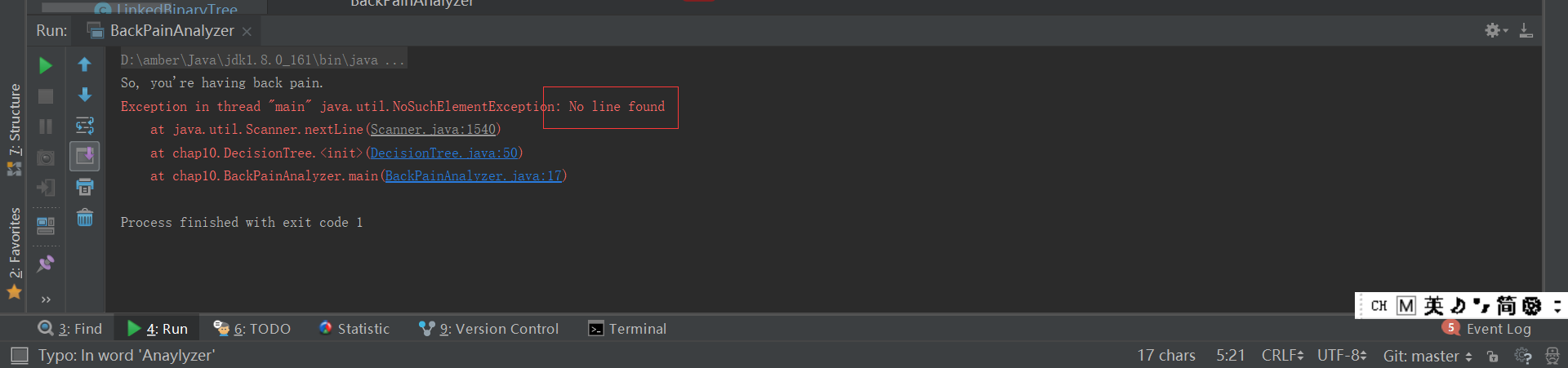
  • 问题一解决方案：
    我无法解决...
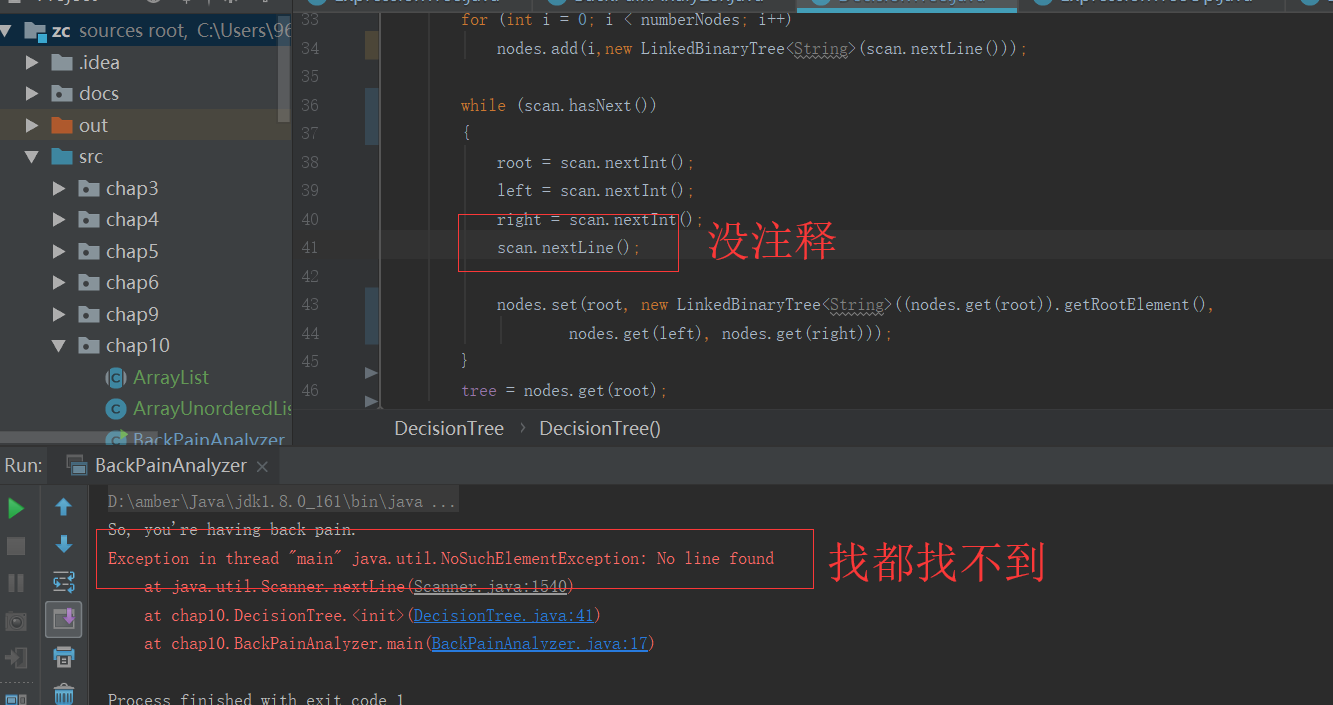
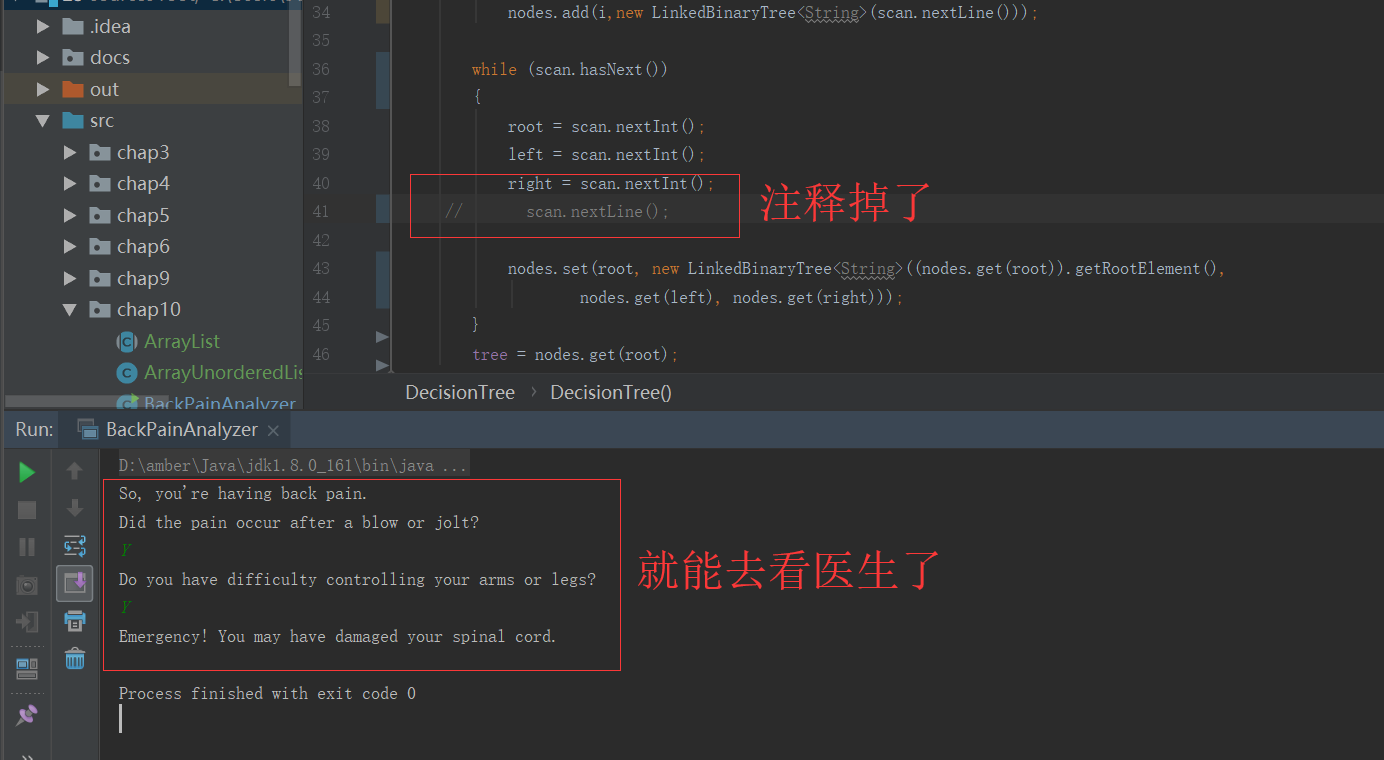
    更新：解决了，但是原因我有一、不太明白为什么。之前和别人对比，代码并没有什么大问题，但是就是提示

Exception in thread "main" java.util.NoSuchElementException: No line found
	at java.util.Scanner.nextLine(Scanner.java:1540)
	at chap10.DecisionTree.<init>(DecisionTree.java:41)
	at chap10.BackPainAnalyzer.main(BackPainAnalyzer.java:17)

不管怎么变，问题就出现在chap10.DecisionTree.(DecisionTree.java:41)中 scan.nextLine();这一行，我实在没办法就想着先把这一句注释了，结果注释之后就可以运行了，但是原因真不太明白

代码托管

上周考试错题总结

上周测试总结上周写了

结对及互评

点评过的同学博客和代码

  • 本周结对学习情况
    • 结对同学学号21
    • 本周结对学习情况
      内容详略得当；
      代码调试环节比较详细，出现得问题都差不多

其他（感悟、思考等，可选）

学习进度条

代码行数（新增/累积） 博客量（新增/累积） 学习时间（新增/累积） 重要成长
目标 5000行 30篇 400小时
第一周 0 1/1 20/20
第二周 300/500 1/2 18/38
第三周 300/600 1/3 18/38
第四周 400/1000 2/5 18/38
第五周 300/1300 1/6 18/38
第六周 300/1300 3/9 18/38

参考资料

posted @ 2018-10-25 15:05  amberR  阅读(248)  评论(1)  编辑  收藏  举报
/*头部导航栏*/ #navigator { font-size:15px; border-bottom: 1px solid #ededed; border-top: 1px solid #ededed; height: 60px;/*导航栏高度，原始50*/ clear: both; margin-top: 25px; } /*导航栏设置,可以自定义导航栏的目录*/ #navList { min-height: 35px; float: left; } #navList li { /*每一个栏目节点*/ float: left; margin: 0 5px 0 0; /*这里原来是0 40px 0 0 */ } #navList a { /*栏目文字的格式*/ display: block; width: 5em; height: 22px; float: left; text-align: center; padding-top: 19px; }