强化学习TD3论文阅读及实验

简介

论文名称：Addressing Function Approximation Error in Actor-Critic Methods

论文地址：https://arxiv.org/abs/1802.09477

论文来源：ICML 2018

针对问题

在value-based强化学习方法，如DQN中，值函数近似误差可能会导致过估计（overestimated）和次优策略。此外，在actor-critic架构的算法中也会存在此类问题。

本文研究

本文提出了Twin Delayed DDPG (TD3)算法，通过引入三个关键技巧来解决这个问题：

• Clipped Double Q-Learning

• Delayed Policy Updates

• Target Policy Smoothing

Clipped Double Q-Learning

尽管之前有许多方法来解决overestimation的问题，但是它们在actor-critic架构中是无效的。

在Double DQN中，将“动作的选择与动作的评估都由target网络来定”这个操作进行“解耦”来减少overestimation，即使用current network来获取a'，使用target network来计算Q(s',a')。在actor-critic架构中也可以使用类似的思想：

\[y=r+\gamma Q_{\theta^{\prime}}\left(s^{\prime}, \pi_{\phi}\left(s^{\prime}\right)\right) \]

但是实际上，由于actor-critic策略更新很缓慢，导致current net与target net非常相似，即\(\pi_\phi(s')\)与\(\pi_{\phi'}(s')\)选择的动作非常相似，从而无法达到“解耦”的目的。

然而原始的Double Q-learning方法却好的效果：

\[\begin{aligned} &y_{1}=r+\gamma Q_{\theta_{2}^{\prime}}\left(s^{\prime}, \pi_{\phi_{1}}\left(s^{\prime}\right)\right) \\ &y_{2}=r+\gamma Q_{\theta_{1}^{\prime}}\left(s^{\prime}, \pi_{\phi_{2}}\left(s^{\prime}\right)\right) \end{aligned} \]

本文也通过实验证明了Double Q-learning的方法确实比Double DQN的方法更能解决overestimation，具体如下：

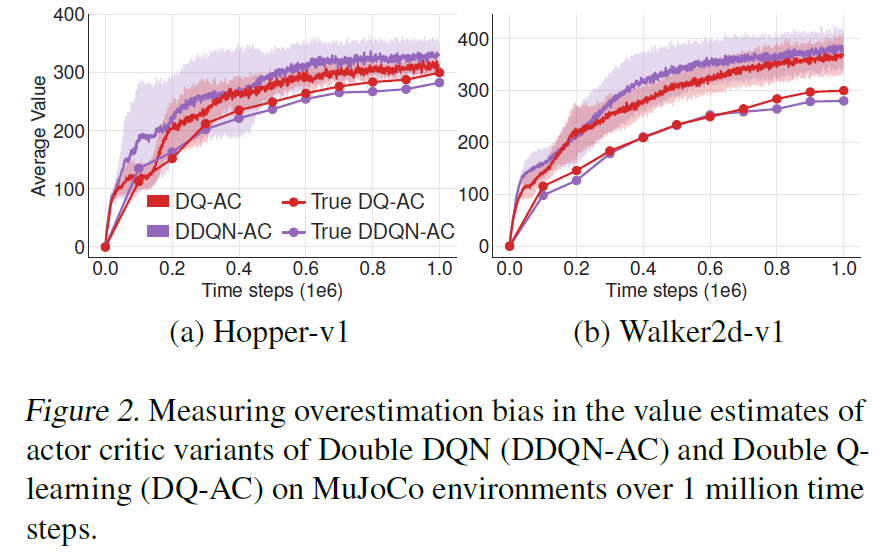
但是直接使用Double Q-learning也是不行的，因为两个critic也不是完全独立的，它们在更新自己时也会用到对方的critic，并且都使用的同一个经验池，也会导致对某些状态的过估计。为了解决这个问题，本文提出了Clipped Double Q-Learning，即取两个Q中小的作为target：

\[y_{1}=r+\gamma \min _{i=1,2} Q_{\theta_{i}^{\prime}}\left(s^{\prime}, \pi_{\phi_{1}}\left(s^{\prime}\right)\right) \]

虽然这个会导致对状态价值的underestimation，但是这远比overestimation要好。

此外，对于policy net只使用一个，即通过\(Q_{\theta_1}\)来更新\(\pi_\phi\)。那么当\(Q_{\theta'_2}>Q_{\theta'_1}\)时，就会选\(Q_{\theta'_1}\)来更新\(Q_{\theta_1}\)，也就是标准的更新，没有额外偏差。当\(Q_{\theta'_2}<Q_{\theta'_1}\)时，就会选\(Q_{\theta'_2}\)来更新\(Q_{\theta_1}\)，表示产生了过估计，用Double Q-learning的思想来解决。

Delayed Policy Updates

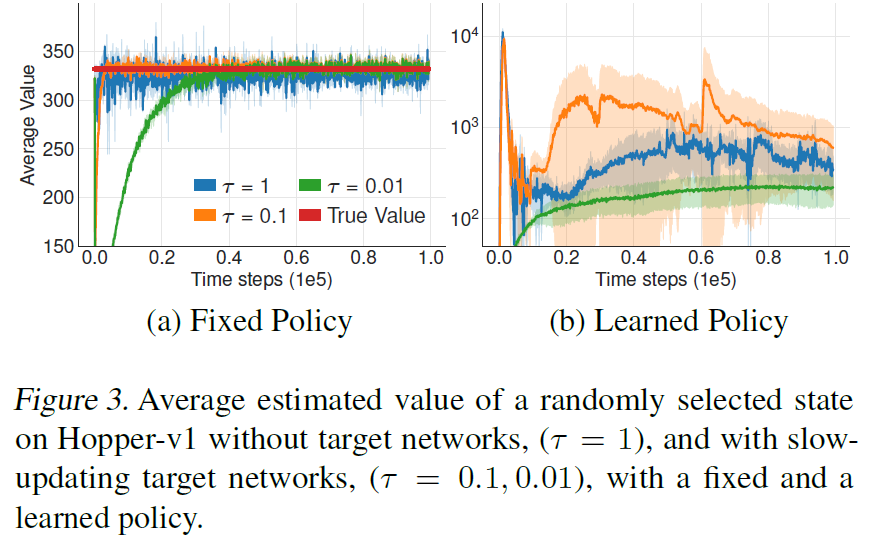
上面解决了高方差引起的overestimation bias，那高方差本身如何解决呢？使用Target net确实可以减少Q值的方差，但是Target net更新的快慢也会影响方差，本文通过如下实验说明了使用更快的Target更新速度(黄色和蓝色线)，会导致高的方差（对Q值的估计波动大）。这种高方差的Q估计会影响policy net的更新，导致策略网络无法收敛。原因是DDPG的policy net也是根据Q来更新的，如果Q一直大幅抖动变化，那么policy net就不知道到底哪个Q是好的，也就是一会Q大，一会Q小的时候，policy net不知道去逼近哪一个了。

因此本文的方法是，让policy net和Target net在Q net更新之后延迟更新，一来保证了Target net更新不那么快，二来使得Q net有一定收敛度之后（方差不那么大之后），再来更新policy net。

Target Policy Smoothing

确定性策略可能会对Target net的局部最优过拟合，因此在计算Target net时给a'加上噪声，使其current net在Target net周围的一定范围内更新。

\[\begin{aligned} y &=r+\gamma \min _{i=1,2} Q_{\theta_{i}^{\prime}}\left(s^{\prime}, \pi_{\phi^{\prime}}\left(s^{\prime}\right)+\epsilon\right) \\ \epsilon & \sim \operatorname{clip}(\mathcal{N}(0, \sigma),-c, c) \end{aligned} \]

注意区分几个noise：

• 采样时，为了增加探索，给actor的结果加上noise。
• 更新critic而计算Target Q时，为了避免过拟合与局部最优，给actor的结果加上noise。
• 更新actor时，因为就是要找使Q值最大的action，所以不需要加noise。

伪代码

实验效果

代码参照Github

在Mujoco的Hopper-v2，HalfCheetah-v2和Walker2d-v2上各训练100万步的训练曲线如下：

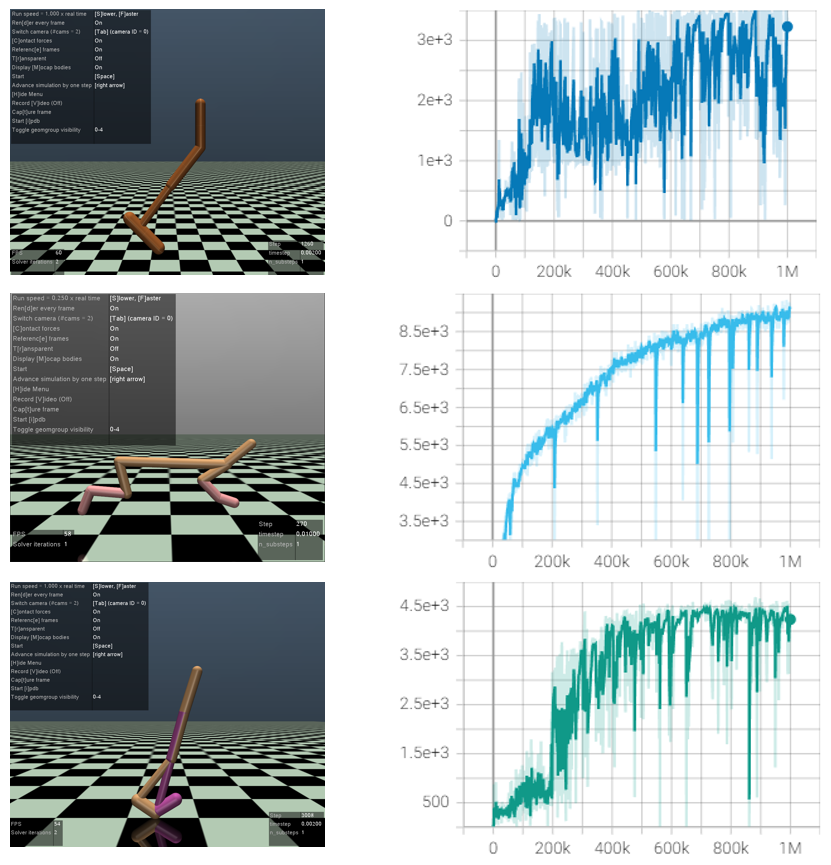
注：本文部分内容仅个人见解，如有错误也欢迎读者批评指正。

参考

https://zhuanlan.zhihu.com/p/111334500
https://spinningup.openai.com/en/latest/algorithms/td3.html
https://blog.csdn.net/weixin_39059031/article/details/104654259