梯度下降做做优化（batch gd、sgd、adagrad ）
首先说明公式的写法
上标代表了一个样本，下标代表了一个维度；
然后梯度的维度是和定义域的维度是一样的大小；
1、batch gradient descent：
假设样本个数是m个,目标函数就是J(theta)，因为theta 参数的维度是和 单个样本 x(i) 的维度是一致的，theta的维度j thetaj是如何更新的呢？？
说明下 这个公式对于 xj(i)
需要说明，这个代表了样本i的第j个维度；这个是怎么算出来的，要考虑 htheta
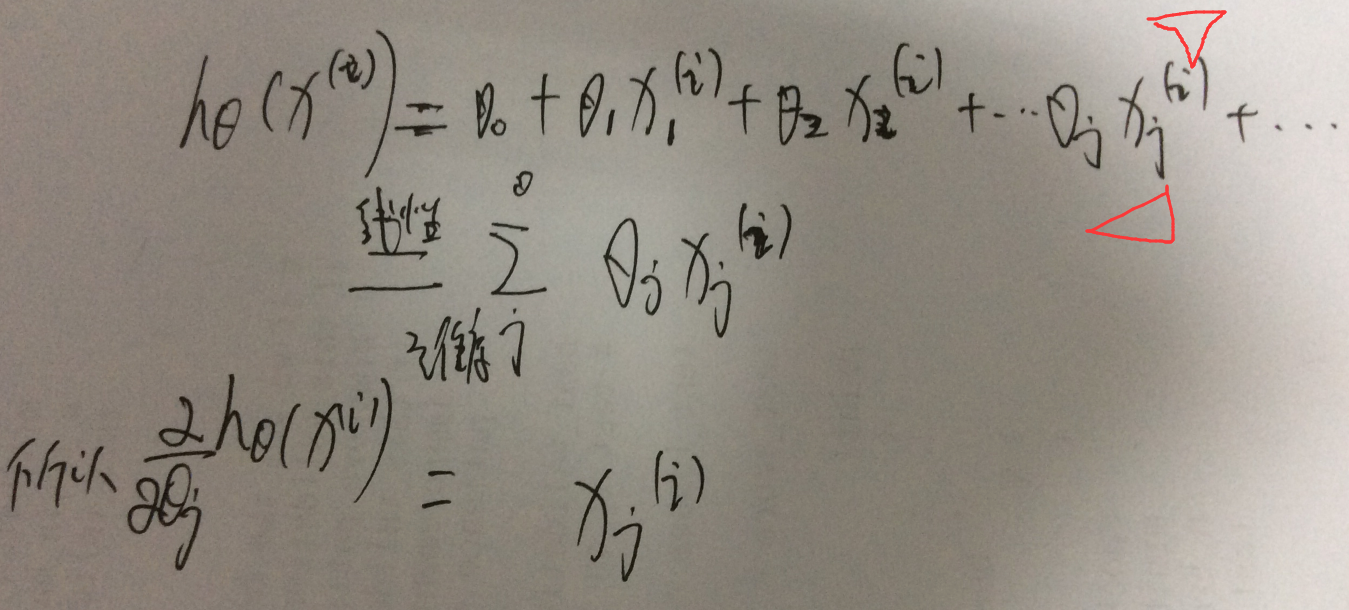
2、SGD
可以看到 theta的一个维度j的一次更新是要遍历所有样本的，这很不科学
转换为 单个样本更新一次，就是sgd
3、什么是adagrad
就是 自适应sgd，是在sgd上的改进
3.1、首先总结sgd的缺点
就是参数 theta的第t+1次更新的时候
使用theta的上一次取值-learning rate* 目标函数C在theta的上一个取值时候的梯度；-----其实梯度是一个向量既有大小也要方向（一维的时候，斜率就是梯度越大代表月陡峭 变化快）----梯度大小代表了变化快慢程度，梯度越大代表变化越快
但是learning raste eta是固定的，这会有问题的，实际希望 eta是可以动态变化的
也就是说如果梯度 steep，那么希望eta 可以小一点，不要走那么快吗！如果梯度 很平滑，那么可以走快一点
3.2、adagrad具体推理过程
4、具体实现：关于sempre中是如何做的？这里传入的梯度是没有做L1之前的梯度
所以总共有三种情况，这里的实现主要是2这种情况；
》》最早的解决L1就是sgd-l1（naive） 是用次梯度
缺点 不能compact 更新所有特征
》》sgd-l1(clipping) 做剪枝
》》sgd-l1(clipping+lazy_update)<=====>sgd-l1(cumulative penalty) 做懒更新
4.1、实现 sgd-l1(clipping)
首先看下 sgd-l1 nonlazy的操作，就是 做 clipping sgd-l1(clipping)，所谓cliping就是对于penalty 做拉成0的操作。
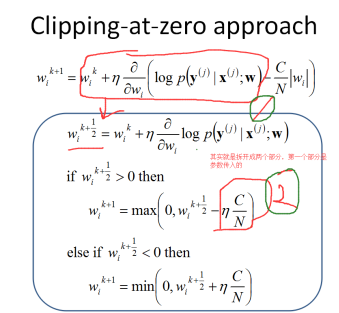
就是简单看下 wi是正还是负，然后取值{1,0,-1},然后那个参数C是控制 the strength of regularization。这种对应的就是 sempre的 nonlzay的情况：
Params.opts.l1Reg = "nonlazy" will reduce the sizes of all parameter weights for each training example, which takes a lot of time.
Adagrad如何计算梯度呢？
