Geometric Deep Learning

看了一遍Geometric Deep Learning 这篇综述。详细看了ChebNet 和Geodesic CNN的原文。

Spetral—fixed domain.

charting – multiple domains. 如果要做shape correspondence 的话GeodesicCNN ,AnisotropicCNN 和MoNet中MoNet效果最好。

讲manifolds的主要是在charting-based methods部分。

第一个问题：shift invariance. 非欧几何没有平移不变性，如图1所示。

 

 

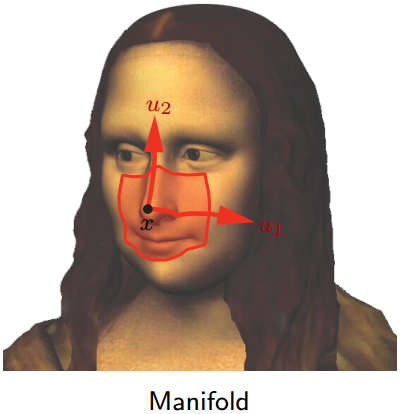
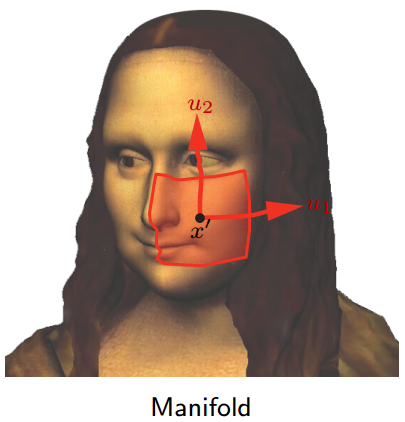
图1 无平移不变性

解决方案：GeodesicCNN中利用polar coordinates 解决了这个问题，如图2所示。

 

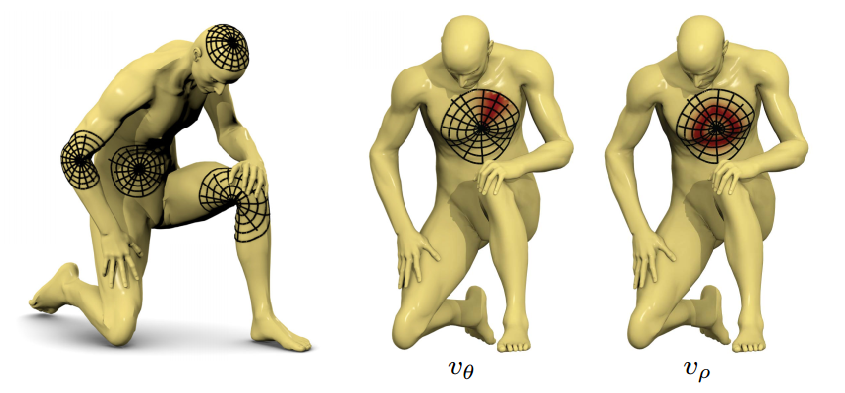
图2. Geodesic CNN

第二个问题：由于将图或流形全局参数化（例如将所有顶点的特征降维到一个向量中）会导致空间信息全部丢失，我们不得不寻找一种表示局部patch的方式。

解决方案：寻找patch的过程就是建立点x的邻域点和x的映射关系，简单的看就是用一系列（J个）加权函数vj(x,x’)来做平均，公式39。这些加权函数可以是各式各样的，geodesic polar coordinates（固定核函数）, anistropic heat kernel, gaussian kernel（高斯混合的协方差矩阵和均值向量都是通过学习得到的）。权重函数的选取可以参考spectrum-free methods 比如利用切比雪夫多项式，便于递归求解进行加速。

 

 

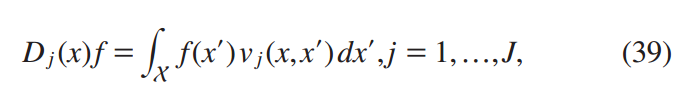
在卷积时也需要patch及参数。