「AHOI2022」山河重整

今年的独立命题除了福建都很一可赛艇啊！

首先有个经典结论是，如果选出的子集 \(S\) 合法，那么 \(\forall i, \sum_{j \in S,j \leq i} j \geq i\)。

那么可以得到一个 \(O(n^2)\) 的 DP。定义 \(dp_{i,j}\) 为在前 \(i\) 个数中，可以构出 \([1,j]\) 内的所有数（第二维与 \(n\) 取最小值），直接转移即可。

陷入困境。一方面这个 DP 的形式不好优化，另一方面容易发现这个 DP 的劣势在于第二维进行了压缩，我们无法得知准确的信息。

那么考虑算不合法的方案数。我们在每一个方案中第一个无法被表示的位置 \(i+1\) 计数。容易发现此时小于等于 \(i\) 的数的和就是 \(i\)。

那么定义 \(f_i\) 为集合 \(\{1,2,\cdots,i\}\) 有多少子集使得和为 \(i\)，且可以表示 \([1,i]\) 内的所有数。遗憾的是在这里我们陷入困境，一方面是直接朴素 DP 和上面的形式毛区别也没有，另一方面可以表示 \([1,i]\) 内的所有数这个限制非常的离谱。

但是，注意到和为 \(i\) 这个限制，并且选出的数都不相同，容易发现我们选出来的数是 \(O(\sqrt n)\) 级别的，并且避免了信息的压缩。那我们转换计数视角，下面给出一个实例：

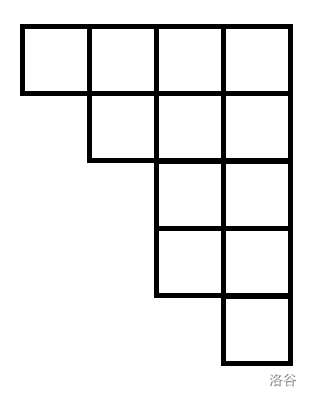
容易发现我们选择了 \(S=\{1,2,4,5\}\)，和为 \(12\)。其中大小不同的行数量级别为 \(O(\sqrt{12})\)。（也可以按整数拆分选择的不同数个数这个角度来考虑。）

那么考虑我们之前 DP 的实质，我们是每次加入一列。那么这里我们按行来考虑。发现这个图有如下特点：

• 行的最大值是 \(O(\sqrt n)\) 的，已经强调了很多次了；
• 上面的行大小都不小于下面的行；
• 如果大小为 \(i\) 的行出现了，那么大小在 \([1,i-1]\) 内的行都出现了。

根据实际意义容易发现到上面的结论。

注意到我们直接计算 \(f_i\) 仍然困难，因为可以表示 \([1,i]\) 内的所有数这个限制确实比较难处理。我们考虑容斥，先算出一个不考虑这个限制的 \(f_i\)。

如何算这个不带限制的 \(f_i\) 呢？容易发现每个大小的行可以出现任意次，类似于完全背包，区别在于带了类似「如果要选 \(i\)，必须先选 \([1,i-1]\) 内的每个数至少一次」限制。那么我们考虑从大的数选起，每次枚举到 \(i\) 的时候为了保证更上面的方案是合法的，我们先选择一个 \(i\)，然后再更新。

	// 此时 f[0] 不等于 1
	for(int i=n;i;--i)
	{
		if(LL(i)*(i+1)/2>n)	continue;
		// 从大的开始选，要保证 i 一定要被选到。从小的开始选的话可能会缺。考虑实际意义，因为 1~p 都要被选到才合法。
		for(int j=n;j>=i;--j)	f[j]=f[j-i];
		// 我先单选个 i，保证之前选择的方案合法
		++f[i];
		for(int j=i;j<=n;++j)	add(f[j],f[j-i]);
		// 做完全背包。
	}
	f[0]=1;

那么对每个 \(i\) 考虑容斥掉不合法的方案数，得到正确的 \(f_i\)。

先考虑对 \(i\) 有贡献的 \(j\)。首先为了方便计数，并且为了满足定义，显然我们后来选的最小的数为 \(j+2\)（因为我们要满足选之后，\(j+1\) 是最小的不能被构出的数，并且和为 \(i\)）。那么不难发现对 \(i\) 有贡献的 \(j\)，满足 \(2j+2 \leq i\)。

注意到这个点，我们在处理 \(f_{1 \sim n}\) 的时候，可以先处理 \(f_{1 \sim \frac{n}{2}}\)，然后继续处理后面的东西。

那么我们已经知道了前面一半的 \(f\)，要求后面一半。

这个时候继续考虑加入每一行之类的想法就非常的没有前途（主要是我没找到）。注意到我们现在要的是，通过选择 \([j+2,i]\) 里面的数，使得和为 \(i-j\)。我们考虑划分数相关的想法。

假设没有选择的数限制（但是还是有选择的数不能重复的限制），不妨写作生成函数的形式：

\[F(x) = \prod_{i=1}^{∞} (1+x^i) \]

再来考虑这个东西的意义……我们按上面的方格图的形式把它排好，然后第 \(i\) 列从下往上删去 \(i\) 个方格（可以发现不会发现没东西删的情况，因为第 \(i\) 列的格子数显然不小于 \(i\)），容易发现上面的行仍然大于等于下面的行，当然这没有什么用。现在减去这个之后形式变成了类似于整数拆分的形式，并且有限制选择的最大的数。

那么，枚举选择的集合的大小：

\[F(x) = \sum_{i=1}^∞ x^{\frac{i(i+1)}{2}} \prod_{j=0}^{i} \dfrac{1}{1-x^j} \]

不难发现 \([x^{i-j}]F(x)\) 就是没有限制的情况下我们要的结果。

但是现在带限制。首先上界我们不用管，可以考虑对 \(x^n\) 之类的东西取模；主要的是下界 \(j+2\)，在我们上面设计的模型下相当于每一列多了 \(j+1\) 个格子，只跟 \(j+1\) 有关系。

记 \(F_p(x)\) 为下界为 \(p+1\) 时的生成函数，那么有：

\[\begin{aligned} F_p(x) &= \prod_{i=p+1}^∞ (1+x^i) \\ &= \sum_{i=1}^∞ x^{\frac{i(i+1)}{2}} x^{ip} \prod_{j=0}^i \dfrac{1}{1-x^j} \end{aligned} \]

再记生成函数 \(G(x)\) 表示一下需要减去的贡献：

\[G(x) = \sum_{j=0}^{n} f_j x^j F_{j+1}(x) \]

把 \(G\) 求出来，更新 \(f\) 的后一半即可。

注意到计算 \(F_p(x)\) 的过程中，\(i\) 的上界为 \(O(\sqrt n)\)，后面 \(\prod\) 内的内容是完全背包（感觉可以和一开始的做法产生有机联系，可惜我没有发现），可以做到 \(O(n \sqrt n)\)。

可以采用其他的手段得到更优的做法。

Key observation: 正难则反，视角转换，生成函数。

int f[500005],g[500005];
void Solve(int n)
{
	if(n<=1)	return ;
	Solve(n/2);
	for(int i=1;i<=n;++i)	g[i]=0;
	for(int i=n;i;--i)
	{
		if(LL(i)*(i+1)/2>n)	continue;
		for(int j=n;j>=i;--j)	g[j]=g[j-i];
		for(int j=0,t=j+(j+2)*i;t<=n;++j,t=j+(j+2)*i)	add(g[t],f[j]);
		for(int j=i;j<=n;++j)	add(g[j],g[j-i]);
	}
	for(int i=n/2+1;i<=n;++i)	sub(f[i],g[i]);
}
int main(){
	int n=read();
	MOD=read();
	for(int i=n;i;--i)
	{
		if(LL(i)*(i+1)/2>n)	continue;
		for(int j=n;j>=i;--j)	f[j]=f[j-i];
		++f[i];
		for(int j=i;j<=n;++j)	add(f[j],f[j-i]);
	}
	f[0]=1;
	Solve(n);
	int ans=1;
	for(int i=0;i<n;++i)	add(ans,ans),sub(ans,f[i]);
	write(ans);
	return 0;
}