Lyndon Word 学习笔记
浅谈 \(\text{Lyndon Word}\)
前置知识,约定与定义
\(\text{Lyndon Word}\) 的学习似乎并不需要太多的前置芝士,但是如果在进阶的时候不学一些基础的字符串算法会比较麻烦,在此之前请保证自己会拓展 KMP,后缀数组,最小表示等一些基础字符串算法,有些可能还会比较冷门。
一个字符可以看成一个长度为 \(1\) 的字符串。
字符和字符串没有特别区分,注意区别。
对于一个字符串 \(s\),记其长度为 \(|s|\)。对于两个字符串 \(u,v\),记 \(uv\) 为两个字符串按顺序拼接成为的新字符串,对于 \(n\) 个字符串 \(s_1,s_2,\dots,s_n\),同理记 \(s_1s_2\dots s_n\) 为 \(n\) 个字符串拼接形成的新字符串。请注意,\(s_is_{i+1} \dots s_j\) 有特别区分 \(s[i\dots j]\) 这一部分。如果单取一个字符串 \(s\) 中的第 \(x\) 个字符,则直接写为 \(s[x]\)。
定义 \(\operatorname{pre}(s,x)\) 为 \(s\) 的前缀,长度为 \(x\);\(\operatorname{suf}(s,x)\) 为 \(s\) 的后缀,长度为 \(x\)。真前缀定义为对于字符串 \(s\),使得\(v=\operatorname{pre}(s,x)\) 且 \(x \neq |s|\),\(v\) 即是 \(s\) 的真前缀,真后缀同理。
若 \(0 \leq r < |s|\),满足 \(\operatorname{pre}(s,r)=\operatorname{suf}(s,r)\),即称 \(\operatorname{pre}(s,r)\) 为 \(s\) 的 \(\operatorname{border}\)。长度为 \(k\) 的 \(\operatorname{border}\) 即 \(\operatorname{pre}(s,k)=\operatorname{suf}(s,k)\)。
对于一个字符串 \(s\),\(s^r\) 为它的反串。
对于一个字符串 \(s\),\(s^a\)(\(a\) 为一个具体数值)表示 \(a\) 个 \(s\) 相拼接。
定义
\(\text{Lyndon Word}\) 定义
定义一个字符串 \(s\) 为 \(\text{Lyndon Word}\),当且仅当 \(s\) 是所有后缀中最小的。
简单来说,如果 \(s\) 满足其最小后缀为 \(s\) 本身的串,即为 \(\text{Lyndon Word}\)。也就是 \(\forall i \in [1,|s|),s<\operatorname{suf}(s,i)\)。
在 Wiki 上还有另外一个等价的定义:\(s\) 是其所有循坏位移中最小的一个。相对来说上面那个会好理解一些。
\(\text{Lyndon}\) 分解定义
\(\text{Lyndon}\) 分解即是将字符串 \(s\) 分解成 \(s_1,s_2,\dots ,s_n\),使得 \(\forall i \in [1,n],s_i\) 为 \(\text{Lyndon Word}\),并且 \(\forall 1 \leq i < n:s_i \geq s_{i+1}\)。
性质
引理 1
若两个字符串 \(u,v\) 为 \(\text{Lyndon Word}\) 并且 \(u<v\),则 \(uv\) 同为 \(\text{Lyndon Word}\)。
证明:
考虑分类讨论长度大小关系:
1,若 \(|u|>|v|\):
因为 \(v\) 是一个 \(\text{Lyndon Word}\),所以 \(v\) 的所有后缀大于 \(v\);考虑证明 \(v>uv\),因为 \(v>u\),显然;
2,若 \(|u| \leq |v|\):
- 如果 \(u\) 不是 \(v\) 的前缀,显然 \(v>uv\);
- 如果 \(u\) 是 \(v\) 的前缀,若 \(uv\) 不为 \(\text{Lyndon Word}\),也就是 \(v<uv\),则有 \(\operatorname{suf}(v,|v|-|u|)<v\),而这和 \(v\) 是 \(\text{Lyndon Word}\) 矛盾,故得证。
引理 2
\(\text{Lyndon}\) 分解唯一。(唯一性)
证明:
假设有两种 \(\text{Lyndon}\) 分解使得分解不唯一,则:
同时有:
假设 \(|s_i| > |s_i'|\),且令 \(s_i=s_i's_{i+1}'\dots s_k' \operatorname{pre}(s_{k+1}',l)\),所以有 \(s_i < \operatorname{pre}(s_{k+1}',l) \leq s_{k+1}' \leq s_i' <s_i\),推出矛盾,故分解唯一。
引理 3
对于每一个字符串,都有其 \(\text{Lyndon}\) 分解。(存在性)
证明:
假设在开始的时候有 \(n\) 个长度为 \(1\) 的字符串 \(s_1,s_2,\dots ,s_n\),我们对于每一次合并,只需要将相邻的两段 \(s_i < s_{i+1}\) 进行合并就行了。
引理 4
如果字符串 \(v\)(\(|v|=r-1\)) 与某个字符串 \(c\)(\(|c|=1\)),满足 \(vc=\operatorname{pre}(s,r)\)(满足 \(s\) 是一个 \(\text{Lyndon Word}\)),则对于一个字符串 \(d\)(\(d>c\) 并且 \(|d|=1\)),使得 \(vd\) 是一个 \(\text{Lyndon Word}\)。
证明:
设 \(s=vct\),则 \(\forall i \in[2,|v|],\operatorname{suf}(v,|v|-i+1)ct>vct\),因而 \(\operatorname{suf}(v,|v|-i+1)c\geq v\)。且 \(d>c\),所以 \(\operatorname{suf}(v,|v|-i+1)d>\operatorname{suf}(v,|v|-i+1)c\geq v\)。
因为 \(\forall i \in [1,|v|]:c>v[i]\),所以有 \(d>c>v[1]\),得证。
引理 5
设有三个字符串 \(s_1,s_2,s_3\),其中 \(s_1\) 是一个 \(\text{Lyndon Word}\) 并且 \(s_1>s_2\geq s_3\)。那么 \(s_1>s_2^2\geq s_2+s_3\)。
证明:
- 如果 \(s_2\) 为 \(s_1\) 的后缀,根据定义有 \(s_1>\operatorname{pre}(s_1,|s_2|)>s_2 \geq s_3\),成立;
- 如果 \(s_2\) 不为 \(s_1\) 的后缀,显然成立。
性质 1
如果 \(s\) 为 \(\text{Lyndon Word}\),则 \(s\) 不存在 \(\operatorname{border}\)。
证明:
如果 \(s\) 存在 \(\operatorname{border}\),则根据 \(\operatorname{border}\) 的定义,存在某个前缀等于后缀,因此这个后缀小于整个串,得证。
性质 2
如果 \(s\) 是 \(\text{Lyndon Word}\),\(s=uv\) 且 \(|u|>0,|v|>0\),满足 \(u<v\)。
\(u<uv\) 而 \(uv<v\),所以 \(u<v\)。
性质 3
如果 \(|s|>2\),\(s\) 是一个 \(\text{Lyndon Word}\) 充要条件是满足 \(s=uv\),且 \(|u|>0,|v|>0,u<v\) 并且 \(u,v\) 都是 \(\text{Lyndon Word}\)。
证明:
-
充分性:查引理 1;
-
必要性:
假设有字符串 \(s\) 有后缀 \(\operatorname{suf}(s,|s|-i+1)\),满足其是 \(s\) 的次小后缀。
又假设 \(\operatorname{pre}(s,i-1)\) 有长度为 \(k\) 的 \(\operatorname{border}\),而 \(k<i-1\),所以 \(k+1 \neq i\)。
因为 \(s\) 是 \(\text{Lyndon Word}\),而 \(\operatorname{suf}(s,|s|-i+1)\) 是其次小后缀,所以 \(\operatorname{suf}(s,|s|-i+1)<\operatorname{suf}(s,|s|-k)\),所以 \(\operatorname{suf}(s,|s|-i+k+1)<s\),与假设 \(s\) 是一个 \(\text{Lyndon Word}\) 矛盾,所以假设不成立,\(\operatorname{pre}(s,i-1)\) 没有 \(\operatorname{border}\)。
根据 \(s\) 是一个 \(\text{Lyndon Word}\) 和 \(\operatorname{pre}(s,i-1)\) 没有 \(\operatorname{border}\) 可以推出:\(\forall 1<j \leq i-1\),\(\exists j \leq k \leq i-1\),满足 \(s[k]>s[k-j+1]\),也就是 \(s[j\dots i-1]>\operatorname{pre}(s,i-1)\),所以 \(\operatorname{pre}(s,i-1)\) 是一个 \(\text{Lyndon Word}\)。
而 \(\operatorname{suf}(s,|s|-i+1)\) 是 \(s\) 的次小后缀,不存在 \(j>i\),使得 \(\operatorname{suf}(s,|s|-j+1)<\operatorname{suf}(s,|s|-i+1)\),所以 \(\operatorname{suf}(s,|s|-i+1)\) 是一个 \(\text{Lyndon Word}\)。
综上,因为 \(s=\operatorname{pre}(s,i-1)\operatorname{suf}(s,|s|-i+1)\),而 \(\operatorname{pre}(s,i-1)\) 和 \(\operatorname{suf}(s,|s|-i+1)\) 均为 \(\text{Lyndon Word}\),得证。
证明了这些性质,主要是用于介绍下面的算法及题目。
算法
不难想到 二分+Hash 和 后缀数组 的做法,下面只介绍专用的算法。
\(\text{Duval}\) 算法
\(\text{Duval}\) 算法可以在 \(O(n)\) 的时间复杂度和 \(O(1)\) 的额外空间复杂度求出一个串的 \(\text{Lyndon}\) 分解。
在整个算法流程中维护三个变量 \(i,j,k\)。\(i\) 的意思是接下来开始划分的位置,意为 \([1,i-1]\) 区间内的字符都已经划分成功。
类似于维护一个循环不变式:
-
\(\operatorname{pre}(s,i-1)=s_1s_2\dots s_g\) 已经固定,且满足 \(s_l\) 为 \(\text{Lyndon Word}\),并且 \(s_l \geq s_{l+1}\);
-
\(s[i \dots k-1]=t_1t_2\dots t_hv(h\geq 1)=t^hv\) 还没有固定,满足 \(t_1\) 是 \(\text{Lyndon Word}\),\(t_1=t_2=\dots=t_h\),\(v\) 是 \(t_h\) 的真前缀,且有 \(s_g \gg s[i,k-1]\)。

这里就直接截 pdf 里面的图了。(其实是懒)
由图可见,\([1,i-1]=s_1s_2\dots s_g\) 已经分解完毕,\([i,k-1]=t^hv\),我们正准备加入 \(k\)。
流程可以表示成维护指针 \(j \gets i,k \gets i+1\),循环分类判断:
- 若 \(a[k]>a[j]\),由引理 4 得到 \(v+s[k]\) 为一个 \(\text{Lyndon Word}\)。根据 \(\text{Lyndon}\) 分解的要求,必须 \(s[i] \geq s[i+1]\),则往前合并,所以 \(j \gets i,k \gets k+1\);
- 若 \(a[k]=a[j]\),有一定可能比原来的小,\(j \gets j+1,k \gets k+1\),继续查找,周期保持;
- 否则这里一定要进行划分,\(t_h\) 固定,退出循环,重新开始。
可以证明一个字符最多经过 \(3\) 次,因此时间复杂度为 \(O(n)\)。
真·板子题。
#include<cstdio>
#include<cstring>
char s[5000005];
int main(){
scanf("%s",s+1);
int len=strlen(s+1);
int i,j,k,ans=0;
i=1;
while(i<=len)
{
for(j=i,k=i+1;k<=len && s[k]>=s[j];++k)
if(s[k]>s[j]) j=i;
else ++j;
while(i<=j) ans^=(i+k-j-1),i+=k-j;
}
printf("%d",ans);
return 0;
}
另外,这个算法可以用同样的思路求出所有 \(s\) 前缀字符串的最大/小的后缀。可以自己思考上手实验。
从入门到进阶
因为这道题实在是钛毒瘤啦,于是借鉴了一下 wcstdio 与 xht37 的题解。
分类讨论。下文中的 \(n=|s|\)。
\(k=1\)
输出 \(s\) 与 \(s^r\) 两个间小的一个。
\(k=n\)
相当于每一个字符都有反转的机会。现在要求的问题是给定 \(s^r\),每次截取一个后缀,拼接于当前字符串之后。显然可以使用 \(\text{Lyndon}\) 对 \(s^r\) 进行分解。
\(k<n\)
相比 \(k=n\) 的情况,我们的操作没有那么随心所欲了。分析发现有两种情况可以合并:
- 若截取的字符串相同,两次操作合并为一次;
- 若截取的字符串都是回文串,两次操作合并为一次并进行反转。
\(k>2\)
有了上面发现的情况,我们考虑指定一个策略进行执行:
设 \(s^r\) 的 \(\text{Lyndon}\) 分解为 \(s_1,s_2,\dots,s_p,t_1,t_2,\dots ,t_q\),满足 \(s_p \not = t_1 = t_2 = \cdots = t_q\)(多次加入相同字符串)或者 $|s_p|>|t_1|=|t_2|=\cdots = |t_q| =1 $(这个字符串长度为 \(1\),一定满足其为回文串)。取出 \(t_1t_2\dots t_q\),接下来继续按这个策略执行。直至 \(k \leq 2\)。同时我们可以发现,\(k=n\) 的特殊情况也是这样的。
\(k \leq 2\)
\(k=1\)
上文已经讨论。
\(k=2\)
现在我们把字符串分成两个部分。继续分情况讨论。
- 两部分都反转。
即 \(s\)。
- 两部分都不反转。
即 \(s^r\) 的最小表示。
- 第一部分反转,第二部分不反转。
枚举字符串断开的位置。反转后缀取最优答案。直接处理是 \(O(n^2)\) 的,我们可以考虑使用拓展 \(\text{KMP}\) 算法(即 \(\text{Z-Algorithm}\))预处理,达到 \(O(1)\)。
原问题可以转化为 \((s^r[i,j-1])^r+\operatorname{pre}(i-1)\) 与 \(s^r\) 的字典序。这个问题可以通过两次询问解决:
- \((s^r[i,j-1])^r\) 与 \(s^r\) 的字典序;
- \(s^r[j-i+1,j-i]\) 与 \(s^r\) 的字典序。
两个问题都与 \(s^r\) 有关,所以说可以用拓展 \(\text{KMP}\) 算法解决这个问题。
- 第一部分不反转,第二部分反转。
设 \(s^r\) 的 \(\text{Lyndon}\) 分解为 \(a_1^{x_1}a_2^{x_2}\dots a_e^{x_e}\),令 \(b_i=a_i^{x_i}\),满足 \(a_1>a_2>\cdots>a_e\)。又令 \(B(i)=b_ib_{i+1} \dots b_e\)。
性质 1:存在整数 \(f \in [1,e]\),使得 \(t_1=B(f)\) 并且答案最优。
这条性质等价于在 \(b_g,b_{g+1}(1 \leq g \leq e-1)\) 间进行划分能够得到最优解。
证明:
- 如果截取的位置恰巧在 \(a\) 的分割线上,那么分割线左右都是两个相等的串 \(a_k\)。这样的话这个 \(a\) 的两个端点至少有一个答案不会更差;
- 如果截取的位置不在 \(a\) 的分割线上,假设截取的位置在 \(a_k\) 中间。因为 \(a_k\) 是 \(\text{Lyndon Word}\),所以截取的位置可以往左挪动直到 \(a\) 的分割线上更优。
性质 2:\(B(i)>B(i+1)\)。
根据引理 5 得证。
根据这个性质,我们可以得到更多的东西。观察发现,取最后一个使得 \(B(p)\) 不是 \(B(p-1)\) 的前缀的 \(p\),因为前面已经讨论得到了 \(t_1=B(p)\) 优于前面的任何 \(B(i)\)。即若最优答案中 \(t_1=B(i)\),满足 \(i \geq p\)。
性质 3:\(|B(i+1)| \leq \dfrac{|B(i)|}{2}\)。
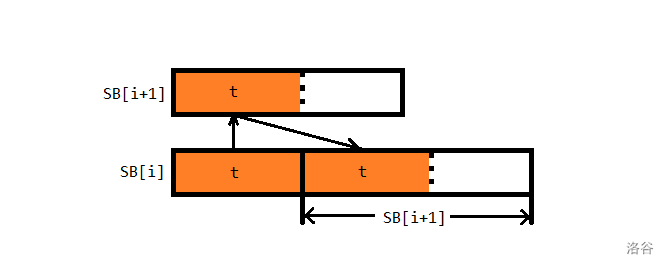
(图源 wcstdio,其中的 \(SB_i\) 即 \(B(i)\))
\(B(i)\) 前面出现了两个 \(t\),但是 \(t=b_i=a_i^{x_i}\),矛盾推出。
根据定理 3,我们能够得到一个优秀的算法——我们只需要找到最大的 \(q\) 使得 \(B(q)\) 比 \(B(q-1)\) 优秀即可。令 \(t_1=B(q)\),此时的答案最优。
于是我们考虑从 \(B(m)\) 开始往前暴力比较,时间复杂度 \(O(n)\)。
综上,问题解决。如果有问题再评论区说说吧。。。思路打完一遍都不敢检查了。
代码太丑不敢放了。/kk
参考文章
如有不对请指出。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号