Normal Equation
一、Normal Equation
我们知道梯度下降在求解最优参数\(\theta\)过程中需要合适的\(\alpha\),并且需要进行多次迭代,那么有没有经过简单的数学计算就得到参数\(\theta\)呢?
下面我们看看Ng 4-6 中的房价预测例子:
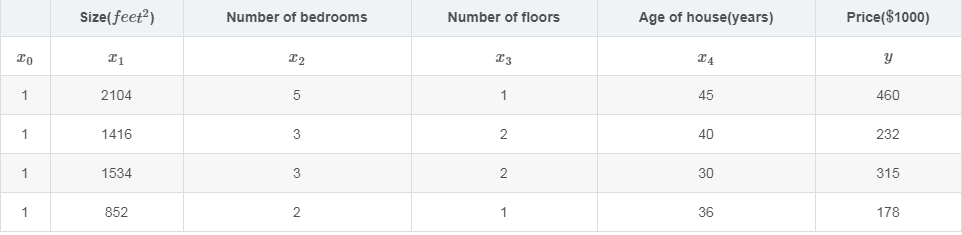
其中\( m = 4, n = 4 \)。在机器学习中,线性回归一般都增加额外的一列特征\(x_0 = 1\),其中我们特征矩阵\(X\)和值向量\(y\)分别为:
\begin{bmatrix}1 & 2104 & 5 & 1 & 45 \\ 1 & 1416 & 3 & 2 & 40 \\ 1 & 1534 & 3 & 2 & 30 \\ 1 & 852 & 2 & 1 & 36 \end{bmatrix}
\begin{bmatrix}460\\ 232\\ 315\\178\end{bmatrix}
而我们的参数\(\theta\)为:
\begin{bmatrix}\theta_0\\ \theta_1\\ \theta_2\\ ...\\\theta_n\end{bmatrix}
那最终的参数\(\theta\)应该为:
\(\theta = (X^TX)^{-1}X^Ty\)
二、证明
我们知道单位矩阵\(E\)有一个性质:
\( A \times A^{-1} = A^{-1} \times A = E \)
首先:
\( y = X \cdot \theta \)
左右同时乘\(X^T\):
\(X^Ty = X^TX \cdot \theta\)
左右再同时乘\(X^TX^{-1}\):
\((X^TX)^{-1}X^Ty = (X^TX)^{-1}X^TX \cdot \theta\)
而我们已知矩阵的逆乘以矩阵得到单位矩阵\(E\):
\((X^TX)^{-1}X^Ty = \theta\)
三、和梯度下降作比较
Normal Equation有一个好处:不需要进行Feature scaling,而Feature scaling对于梯度下降是必须的

如何来选择使用哪种方法么呢?一般如果特征维度不超过1000的话,Normal Equation还是可选的。
此外,如果\((X^TX)^{-1}\)不可逆怎么办?
1)确保不存在冗余特征,比如

因为\(1m = 3.28feet\),所以\(x_1 = (3.28)^2 * x_2\),我们知道线性代数中出现这种线性相关的情况,其行列式值为0,所以不可逆,我们只需确保不会出现冗余特征即可。
2)特征数量\(n\)过多,而样本数量\(m\)过少:解决方法为删除一部分特征,或者增加样本数量。
四、说明



