聚类算法中的距离度量有哪些

一、你知道聚类中度量距离的方法有哪些吗？

　1）欧式距离

　欧氏距离是最易于理解的一种距离计算方法，源自欧氏空间中两点间的距离公式。即两点之间直线距离，公式比较简单就不写了

　应用场景：适用于求解两点之间直线的距离，适用于各个向量标准统一的情况

 

　2）曼哈顿距离(Manhattan Distance)

　从名字就可以猜出这种距离的计算方法了。想象你在曼哈顿要从一个十字路口开车到另外一个十字路口，实际驾驶距离就是这个“曼哈顿距离”。而这也是曼哈顿距离名称的来源， 曼哈顿距离也称为城市街区距离(City Block distance)

　应用场景：主要应用场景，如棋盘、城市里两个点之间的距离等

 

　3）切比雪夫距离 (Chebyshev Distance )

　国际象棋玩过么？国王走一步能够移动到相邻的8个方格中的任意一个（国王可以直行、横行、斜行，但是每次只能动一个格。国王是生命的象征，国王死掉，棋局结束）。那么国王从格子\((x_1,y_1)\)走到格子\((x_1,y_1)\)最少需要多少步？自己走走试试。你会发现最少步数总是\(max(|x_2-x_1|,|y_2-y_1|)\)步 。有一种类似的一种距离度量方法叫切比雪夫距离，公式是：

\( Cdist = max(|x_i - y_i)) \)

　应用场景：计算国际象棋中国王走步

 

　4) 夹角余弦相似度（Cosine）

　夹角越小越相似，\(cos\theta = \frac{a^Tb}{|a||b|}\)

　应用场景：常用于文本识别，比如新闻的挖掘

　举例：

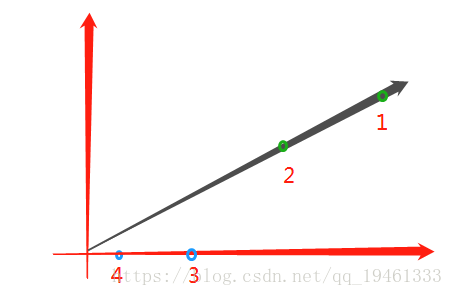
　　文本1中词语a,b分别出现100,50次，向量表示为（100,50）

　　文本2中词语a,b分别出现50,25次，向量表示为（50,25）

　　文本3中词语a,b分别出现10,0次，向量表示为（10,0）

　　文本4中词语a,b分别出现2,0次，向量表示为（2,0）

　　可以得知，1，2点向量平行（词频比例相同），3，4点向量平行，那么是不是可以判断1，2文本更相似，3，4文本更相似呢？

 

　5）Pearson相关系数

　皮尔逊相关系数考察两个变量的关系，值越大，两个变量越近强相关，即距离越近，所以距离：\(dist(X,Y) = 1 - \rho_{X,Y}\)

　\(\rho_{X,Y} = Cov(X, Y)/\sigma_X\sigma_Y = E((X-\mu_X)(Y-\mu_Y))/\sigma_X\sigma_Y\)

 

　6）马氏距离

　用来度量一个样本点P与数据分布为D的集合的距离。

　假设一个样点P为：\(x = (x_1,x_2,x_3,...,x_N)^T\)

　数据集D均值为：\(\mu = (\mu_1,\mu_2,\mu_3,...,\mu_N)^T\)，协方差矩阵是\(S\)

　则这个样本点P与数据集合D的马氏距离为：\(D_M(x) = \sqrt{(x-\mu)^TS^{-1}(x-\mu)}\)

　马氏距离也可以衡量两个来自同一分布的样本x和y的相似性，其中x和y是向量：\(d(x,y) = \sqrt{(x-y)^TS^{-1}(x-y)}\)

　当样本集合的协方差矩阵是单位矩阵时，即样本的各个维度上的方差均为１．马氏距离就等于欧式距离相等。 

　不难发现，如果去掉马氏距离中的协方差矩阵，就退化为欧氏距离。那么我们就需要探究这个多出来的因子究竟有什么含义

　例子：

　　如果我们以厘米为单位来测量人的身高，以克（g）为单位测量人的体重。每个人被表示为一个两维向量，如一个人身高173cm，体重50000g，表示为（173，50000），根据身高体重的信息来判断体型的相似程度。

　　我们已知小明（160，60000）；小王（160，59000）；小李（170，60000）。根据常识可以知道小明和小王体型相似。但是如果根据欧几里得距离来判断，小明和小王的距离要远远大于小明和小李之间的距离，即小明和小李体型相似。这是因为不同特征的度量标准之间存在差异而导致判断出错。

　　以克（g）为单位测量人的体重，数据分布比较分散，即方差大，而以厘米为单位来测量人的身高，数据分布就相对集中，方差小。马氏距离的目的就是把方差归一化，使得特征之间的关系更加符合实际情况。

　　图（a）展示了三个数据集的初始分布，看起来竖直方向上的那两个集合比较接近。在我们根据数据的协方差归一化空间之后，如图（b），实际上水平方向上的两个集合比较接近

 

　为什么马氏距离是与尺度无关的？

　　也许你认为那只要将数据标准化后，不就可以计算距离了吗？但是如果是单纯使每个变量先标准化，然后再计算距离，可能会出现某种错误，原因是可能在有些多维空间中，某个两个维之间可能是线性相关的，协方差矩阵的引入可以去除特征的线性相关性。

 

　7）海明距离

　　在信息领域，两个长度相等的字符串的海明距离是在相同位置上不同的字符的个数，也就是将一个字符串替换成另一个字符串需要的替换的次数。

　　例如：

　　　"toned" and "roses" is 3

　　　1011101 and 1001001 is 2

　　　2173896 and 2233796 is 3

　　海明距离若用于分类变量，如果X与Y的值相同，距离D为0，否则D为1：

\(D_H = \sum_{i=1}^{n}|x_i - y_i|\)

\(x=y => D = 0\)

\(x\neq y => D = 1\)