多维高斯分布
一、一维高斯分布
先来看看一维正态(高斯)分布的公式:\( N(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}exp[-\frac{(x-\mu)^2}{2\sigma^2}] \)
比如对334个人的身高进行统计,如下图:
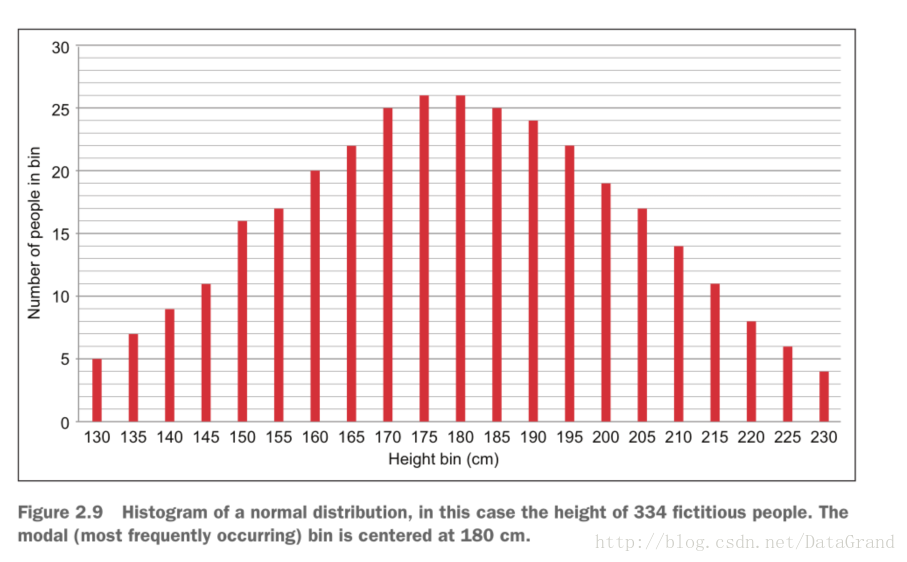
学过大学高数的同学应该还记得,正态分布的一个背景知识点是,95%的数据分布在均值周围2个标准差的范围内。本例中大约20到30左右是标准差参数的取值,均值在180cm左右,因此大多数数据都分布在120cm到240cm之间
上面的一维高斯公式是概率密度函数,也就是在已知参数的情况下,输入变量指x,可以获得相对应的概率密度。还要注意一件事,就是在实际使用前,概率分布要先进行归一化,也就是说曲线下面的面积之和需要为1,这样才能确保返回的概率密度在允许的取值范围内。
如果需要计算指定区间内的分布概率,则可以计算在区间首尾两个取值之间的面积的大小。另外除了直接计算面积,还可以用更简便的方法来获得同样的结果,就是减去区间x对应的累积密度函数(cumulative density function,CDF)。因为CDF表示的是数值小于等于x的分布概率。
二、多维高斯分布
一维拓展到高维:\( N(\bar{x}|\bar{\mu},\sum) = \frac{1}{({2\pi})^{D/2}}*\frac{1}{|\sum|^{1/2}}*exp^{\frac{-(\bar{x}-\bar{\mu})^T*\sum ^{-1}*(\bar{x}-\bar{\mu})}{2}} \)
其中\( \bar{x} \)表示维度为D的向量,\( \bar{\mu} \)表示这些向量的平均值,\( \sum \)表示向量\( \bar{x} \)的协方差矩阵
下面以二维为例,试着推导上面的多维高斯分布公式:
假设所有变量都是相互独立的。即对于概率分布函数\( f(x_1,x_2,...,x_n) \)而言,有\( f(x_1,x_2,...,x_n) = f(x_1)*f(x_2)*...*f(x_n) \)成立,假设存在多个样本,每个样本有两维特征,即每个样本:
\(\bar{x} = \begin{bmatrix}x_1\\ x_2\end{bmatrix}\),他们的均值是:\(\bar{\mu} = \begin{bmatrix}\mu_1\\ \mu_2\end{bmatrix}\),方差是:\(\bar{\sigma } = \begin{bmatrix}\sigma_1\\ \sigma_2\end{bmatrix}\)
由于假设样本得两个特征\(x_1,x_2\)相互独立,所以样本\(\bar{x}\)的高斯分布函数可以表示为:
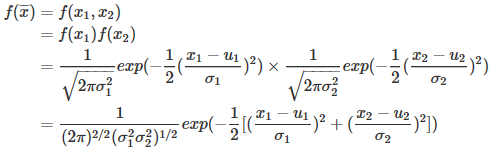
对于二维的向量\(\bar{x}\)而言,其协方差矩阵为:\(\sum = \begin{bmatrix}\sigma_{11} &\sigma_{12} \\ \sigma_{21}& \sigma_{22}\end{bmatrix} = \begin{bmatrix}\sigma_1^2 &0 \\ 0& \sigma_2^2\end{bmatrix}\),注意负对角线由于两个特征相互独立,即没有相关性,结果为0
而\(\sum\)的行列式\(\sum = \sigma_1^2\sigma_2^2\),所以下面的公式成立:
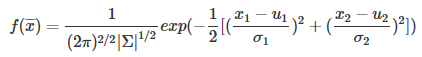
为了帮助理解,穿插一些行列式知识:

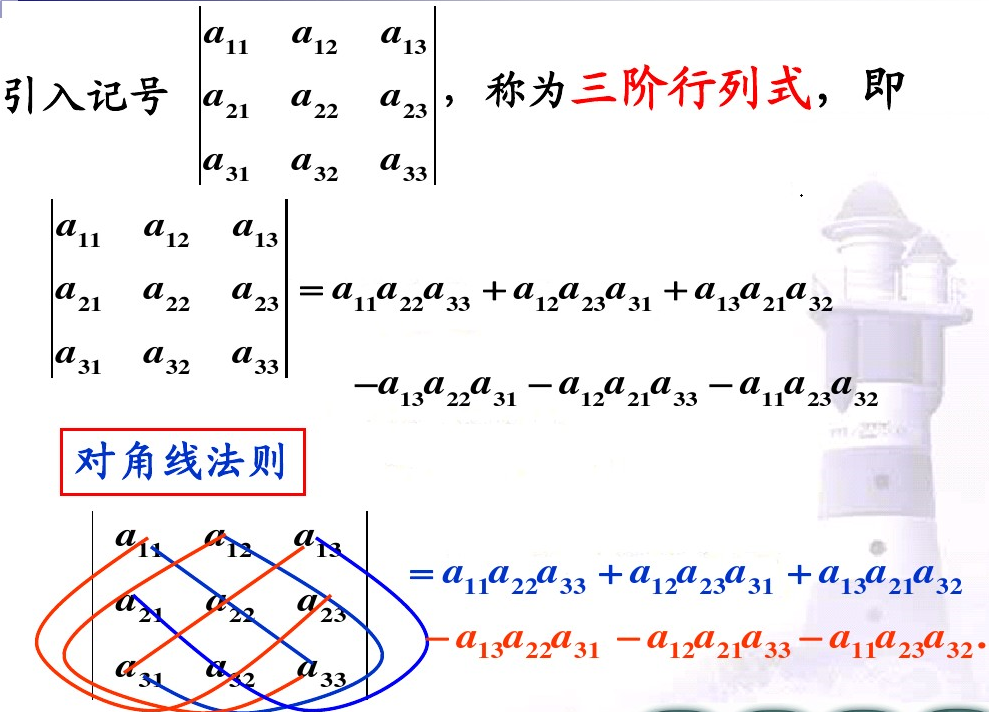
这样一来,我们已经推出了公式的左半部分,下面,开始处理右面的\(exp\)函数:原始的高维高斯函数的\(exp^{\frac{-(\bar{x}-\bar{\mu})^T*\sum ^{-1}*(\bar{x}-\bar{\mu})}{2}}\)
根据前面算出来的\(\sum\),我们可以求出它的逆:\(\sum^{-1} = \frac{1}{\sigma_1^2\sigma_2^2}\begin{bmatrix}\sigma_2^2 &0 \\ 0& \sigma_1^2\end{bmatrix}\)
接下来根据这个二维的例子,将原始的\(exp\)展开:
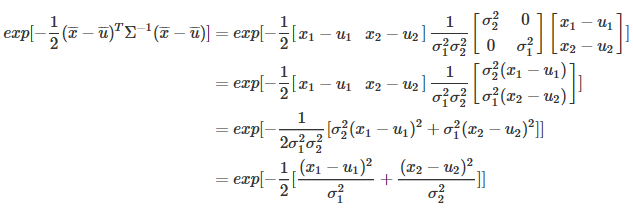
综上,完成了二维高斯混合模型的公式
三、函数的图像
知道多维的公式后,下面再简单比较一下一维和二维的图像区别
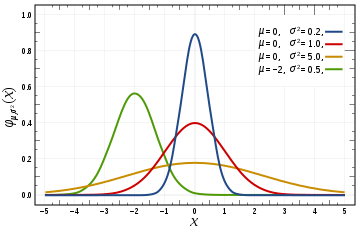
上图展示的是4个一维高斯函数的图像。高斯函数是一个对称的山峰状,山峰的中心是均值\(\mu\),山峰的胖瘦由标准差\(\sigma\)决定,如果\(\sigma\)越大,证明数据分布越广,那么山峰越「矮胖」,反之,则数据分布比较集中,因此很大比例的数据集中在均值附近,山峰越「瘦高」
下面看二维的例子:
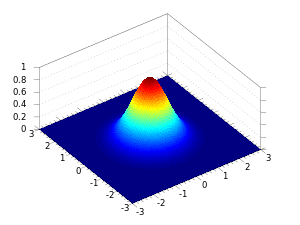
有了一维图像的例子,二维图像就可以类比出来了。如果说,一维只是山峰的一个横截面,那么二维则是一个完整的有立体感的山峰。山峰的「中心」和「胖瘦」和一维的情况是一致的,而且,对于偏离中心较远的位置,数据出现的概率几乎为 0,因此,函数图像在这些地方就逐渐退化成「平原」了。



