正态分布与二项分布

一、什么是正态分布

　Normal Distribution（或者叫高斯分布）是非常常见的连续概率分布。正态分布的概率密度函数为：其中\(\mu\)是分布的均值，或者叫期望值；\(\sigma\)是标准差

\( f(x|\mu,\sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}}e^{-(x-u)^2/(2\sigma^2)} \)

　当\(\mu=0\)和\(\sigma=1\)的时候，正态分布就是标准正态分布了，标准正态分布是关于x=0对称的

　

二、正态分布的表示符号：

　正态分布经常可以用\( N(\mu,\sigma^2)\)来表示，因此，当一个随机变量X是一个均值为\( \mu\)和标准差为\( \sigma\)的正态偏差时，我们可以用这个形式表达：\( X \sim N(\mu,\sigma^2) \)

 

三、概率值

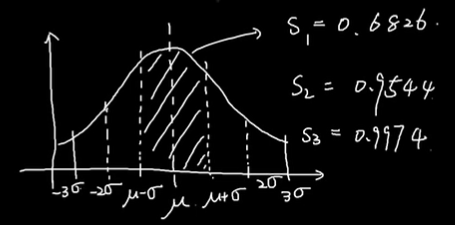
　一个样本落在${\mu-\sigma}$和${\mu+\sigma}$的概率为：0.6826，落在${\mu-2\sigma}$和${\mu+2\sigma}$的概率为：0.9544，落在${\mu-3\sigma}$和${\mu+3\sigma}$的概率为：0.9974

 

四、二项分布

　n次独立重复实验：也叫伯努利实验，由n次实验构成，且每次实验相互独立，并且每次实验的结果只有两种对立状态，$p$和非$p$

　在N次独立重复实验中，事件A恰好发生K次的概率为：$P_n(k)=C_n^kp^kq^{n-k},k=0,1,2,...,n$