K-means

一、K-means

　 非监督学习中有一大类问题是聚类问题，其中有个经典算法:K-means，其中K代表我们事先已经知道要将数据集分成K类 。K-Means算法的思想很简单，对于给定的样本集，按照样本之间的距离大小，将样本集划分为K个簇。让簇内的点尽量紧密的连在一起，而让簇间的距离尽量的大。 原理如下图：

 

二、原理

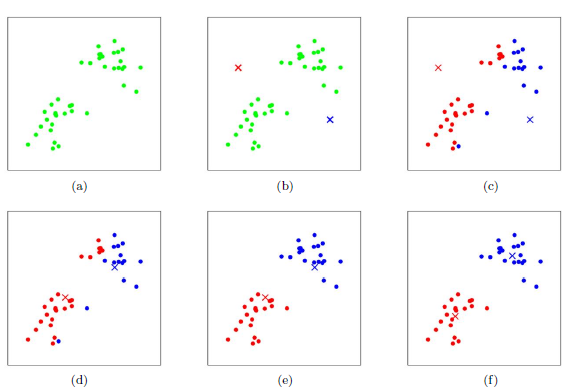
　针对上图：

　　a表达了初始的数据集，假设k=2

　　b中，随机选择了两个k类所对应的类别质心，即图中的红色质心和蓝色质心，然后分别求样本中所有点到这两个质心的距离，并标记每个样本的类别为和该样本距离最小的质心的类别

　　c所示，经过计算样本和红色质心和蓝色质心的距离，我们得到了所有样本点的第一轮迭代后的类别。此时我们对我们当前标记为红色和蓝色的点分别求其新的质心

　　d所示，新的红色质心和蓝色质心的位置已经发生了变动

　　e和图f重复了我们在图c和图d的过程，即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。

 

三、算法分析

　1）K-means算法的第一步需要确定任意的K个初始聚类中心，但实际上所谓的“任意”也有一定的原则，不恰当的选取初始中心点有时候会导致聚类结果并不理想，初始中心的选取也是K-means算法面对的困难之一，一般以彼此相距尽可能大的K个点作为初始中心点.

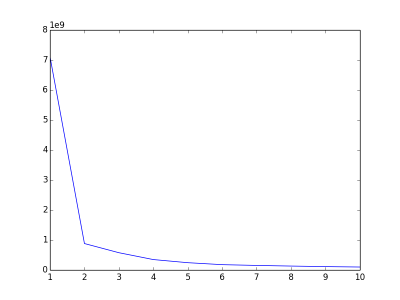
　2）K-means算法还需要面对一个问题：到底这些数据应该分成多少个类型才合适？（即K=？）好的聚类结果应该是：各个聚类彼此间的数据特征差异很大，而聚类内的数据特征差异很小。可以用误差平方和（SSE）作为准则函数来评价，即聚类内各个点到聚类中心的距离的平方和。一般地，在合适的K范围内当SSE越少则聚类结果越好。之所以说“合适的K范围”，是因为当K太大，极端地当K等于数据集的元素个数时，此时每个点都是一个聚类，中心点就是自身，此时SSE=0，这显然不是一个理想的聚类结果。要选出合适的K值，一个常用的方法（The Elbow Method）是计算不同K值下的聚类结果的SSE，画出K-SSE的变化关系，选取发生抖动的那个点所在的值作为K值.（如下图，当k=2时发生了明显的抖动，对于该数据集我们认为K=2是个合适的选择）

 

　3）K-means算法的第二步需要计算两点之间的距离，这个距离实际上是描述了两个点的相异度，评价的方法有很多种，例如：欧几里得距离、曼哈顿距离等，距离计算方法的选取要结合实际的数据特征，并非所有情况都适合用欧几里得距离来衡量二者的相异度，例如对于一个曲面，空间上很接近的两个点，实际上在曲面上的距离可能非常远.

　4）计算距离时需要考虑各个维度的特征值是否会对结果产生异常影响，例如：对于特征点（1，2，3，999）、（1，2，2，888）、（2，3，4，777）可以发现，第四维特征（即999、888、777）会直接主导了整个距离的结果，其他特征的特征值几乎对距离结果没有影响，这显然不符合距离的意义，这时候需要对特征值进行归一化处理.