逻辑回归
3P-2L
一、逻辑回归简介
一句话概括:逻辑回归假设数据服从伯努利分布,通过极大化似然函数的方法,运用梯度下降来求解参数,来达到将数据二分类的目的
这里面其实包含了5个点 1:逻辑回归的假设,2:逻辑回归的损失函数,3:逻辑回归的求解方法,4:逻辑回归的目的,5:逻辑回归如何分类。这些问题是考核你对逻辑回归的基本了解
- 逻辑回归的假设:
逻辑回归的第一个基本假设是假设数据服从伯努利分布。伯努利分布有一个简单的例子是抛硬币,抛中为正面的概率是p,抛中为负面的概率是1-p,逻辑回归需要将线性模型进行一下映射,从而能用于分类
这里的映射函数或者叫分类器叫做sigmoid函数,通过sigmoid函数分类器,逻辑回归的第二个假设是假设样本为正的概率是:
\( P(y=1|x;\theta ) = \frac{1}{1+e^{-z}} = \frac{1}{1+e^{-\theta^Tx}} \)
- 逻辑回归的损失函数:
常用的损失函数有以下几种:
-
- 0-1损失函数:
\(L(Y,f(X)) = \left\{\begin{matrix}1 & Y \neq f(X)\\ 0 & Y = f(X)\end{matrix}\right.\)
-
- 平方损失函数:
\(L(Y,f(X)) = (Y - f(X))^2\)
-
- 绝对损失函数:
\(L(Y,f(X)) = | Y - f(X))|\)
-
- 对数损失函数或对数似然损失函数:
\(L(Y,P(Y|X)) = -logP(Y|X)\)
对于逻辑回归模型,使用的是对数损失函数作为代价函数,则本例中,逻辑回归的损失函数为:
\(cost(y,p(y|x)) = \left\{\begin{matrix}-logp(y|x) & if(y = 1)\\ -log(1-p(y|x))& if(y = 0)\end{matrix}\right.\)
将上面的两个表达式合并,则得到单个数据点上的log损失为:
\(cost(y,p(y|x)) = -ylogp(y|x) - (1-y)log(1-p(y|x))\)
因为y只有两种取值情况,1或0,分别令y=1或y=0,即可得到原来的分段表达式,即两者是等价的。全体样本的损失函数则可表达为:
\(cost(y,p(y|x)) = \sum_{i=1}^{m} -y_ilogp(y_i|x_i) - (1-y_i)log(1-p(y_i|x_i))\)
其中\(p(y|x)\)由前面的逻辑回归模型定义,令:
\(p(y|x) = h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}\)
则最终的损失函数为:
\(cost(y,p(y|x)) = \sum_{i=1}^{m} (-y_ilog\frac{1}{1+e^{-\theta^Tx}} - (1-y_i)log(1-\frac{1}{1+e^{-\theta^Tx}}))\)
即逻辑回归的损失函数是它的极大似然函数:
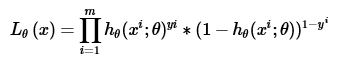
- 逻辑回归的求解方法:
由于该极大似然函数无法直接求解,一般通过对该函数进行梯度下降来不断逼近最优解。因为就梯度下降本身来看的话就有随机梯度下降,批梯度下降,small batch 梯度下降三种方式
- 逻辑回归的目的:
将数据二分类,提高准确率
- 逻辑回归如何分类:
逻辑回归作为回归,如何应用到分类上去?y值确实是一个连续的变量。逻辑回归的做法是划定一个阈值,y值大于这个阈值的是一类,y值小于这个阈值的是另外一类。阈值具体如何调整根据实际情况选择。一般会选择0.5做为阈值来划分。
二、Sigmoid函数
如果我们使用线性回归来预测y的取值。这样做会导致线性回归的结果取值并不为0或1
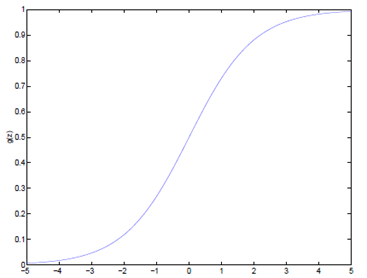
逻辑回归使用一个函数来归一化y值,使y的取值在区间(0,1)内,这个函数称为Logistic函数(logistic function),也称为Sigmoid函数(sigmoid function)。函数公式如下:
\( g(z) = \frac{1}{1+e^{-z}} \)
函数图像如下:
该函数导数有一个特性:

经过Sigmoid函数转换后的y值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
\( P(y=1|x;\theta ) = h_\theta (x) \)
\( P(y=0|x;\theta ) = 1 - h_\theta (x) \)
对上面的表达式合并一下就是:
\( P(y|x;\theta ) = (h_\theta (x))^y(1-h_\theta (x))^{1-y} \)
三、推导过程
梯度上升
构建完似然函数,我们最大似然估计,最终推导出θ的迭代更新表达式
只不过这里用的不是梯度下降,而是梯度上升,因为这里是最大化似然函数不是最小化似然函数。我们假设训练样本相互独立,那么似然函数表达式为:
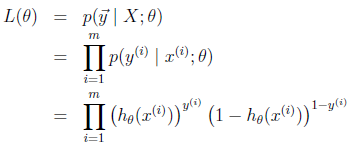
同样对似然函数取log,转换为:

转换后的似然函数对θ求偏导,在这里我们以只有一个训练样本的情况为例:
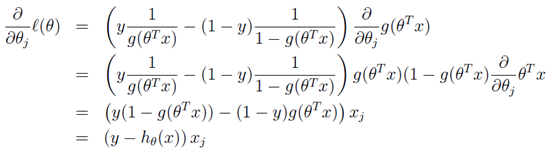
这样我们就得到了梯度上升每次迭代的更新方向,那么\( \theta \)的迭代表达式为:
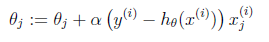
四、逻辑回归参数
逻辑回归的模型调优一般考虑对其正则惩罚项系数进行调整,sigmoid函数的选择,在实际场景中一般是保证一定精确率(Precision)的情况下尽可能提高召回率(Recall rate)
1)class_weight:类型权重参数,默认None,可以输入"balanced"或者一个字典
该参数用于标示分类模型中各种类型的权重,可以不输入,即不考虑权重,或者说所有类型的权重一样
如果选择输入的话,可以选择balanced让类库自己计算类型权重,或者我们自己输入各个类型的权重,比如对于0,1的二元模型,可以定义class_weight={ 0:0.9, 1:0.1 },这样类型0的权重为90%,而类型1的权重为10%
如果class_weight选择balanced,那么类库会根据训练样本量来计算权重。某种类型样本量越多,则权重越低,样本量越少,则权重越高
sklearn的官方文档中,当class_weight为balanced时,类权重计算方法如下:
n_samples / (n_classes * np.bincount(y)),n_samples为样本数,n_classes为类别数量,np.bincount(y)会输出每个类的样本数,例如y=[1,0,0,1,1],则np.bincount(y)=[2,3]
那么class_weight有什么作用呢?在分类模型中,我们经常会遇到两类问题:
第一种是误分类的代价很高。比如对合法用户和非法用户进行分类,将非法用户分类为合法用户的代价很高,我们宁愿将合法用户分类为非法用户,这时可以人工再甄别,但是却不愿将非法用户分类为合法用户。这时,我们可以适当提高非法用户的权重
第二种是样本是高度失衡的,比如我们有合法用户和非法用户的二元样本数据10000条,里面合法用户有9995条,非法用户只有5条,如果我们不考虑权重,则我们可以将所有的测试集都预测为合法用户,这样预测准确率理论上有99.95%
但是却没有任何意义。这时,我们可以选择balanced,让类库自动提高非法用户样本的权重
提高了某种分类的权重,相比不考虑权重,会有更多的样本分类划分到高权重的类别,从而可以解决上面两类问题
2)sample_weight:样本权重参数
由于样本不平衡导致我们的模型预测能力下降。遇到这种情况,我们可以通过调节样本权重来尝试解决这个问题
调节样本权重的方法有两种,第一种是在class_weight使用balanced。第二种是在调用fit函数时,通过sample_weight来自己调节每个样本权重
在scikit-learn做逻辑回归时,如果上面两种方法都用到了,那么样本的真正权重是class_weight * sample_weight
3)penalty:正则化参数:’l1’,’l2’.默认是’l2’
在调参时如果我们主要的目的只是为了解决过拟合,一般penalty选择L2正则化就够了。但是如果选择L2正则化发现还是过拟合,即预测效果差的时候,就可以考虑L1正则化
另外,如果模型的特征非常多,我们希望一些不重要的特征系数归零,从而让模型系数稀疏化的话,也可以使用L1正则化
penalty参数的选择会影响我们损失函数优化算法的选择。即参数solver的选择
4)C:smaller values specify stronger regularization
五、手撕逻辑回归
1)数据获取加header
import pandas as pd
import numpy as np
#数据没有标题,因此加上参数header
df = pd.read_csv('https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/breast-cancer-wisconsin.data',
header=None)
column_names = ['Sample code number', 'Clump Thickness', 'Uniformity of Cell Size',
'Uniformity of Cell Shape', 'Marginal Adhesion', 'Single Epithelial Cell Size',
'Bare Nuclei', 'Bland Chromatin', 'Normal Nucleoli', 'Mitoses', 'Class']
df.columns = column_names
df[df['Sample code number'] == 1057067]
我们发现有些特征存在空值:

去掉空值:
df = df.dropna(how='any') print(df.shape) # 剩下683个样本:(683, 11) df[df['Sample code number'] == 1057067]
可以发现已经不存在这个样本了,已经被去掉了:
![]()
分割数据:
import warnings
warnings.filterwarnings('ignore')
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
#一般1代表恶性,0代表良性(本数据集4恶性,所以将4变成1,将2变成0)
#df['Class'][data['Class'] == 4] = 1
#df['Class'][data['Class'] == 2] = 0
df.loc[ df['Class'] == 4, 'Class' ] = 1
df.loc[ df['Class'] == 2, 'Class' ] = 0
#Sample code number特征对分类没有作用,将数据集75%作为训练集,25%作为测试集
X_train, X_test, y_train, y_test = train_test_split(df[column_names[1:10]], df[column_names[10]],
test_size = 0.25, random_state = 33)
ss = StandardScaler()
X_train = ss.fit_transform(X_train)
X_test = ss.transform(X_test)
X_train = np.round(X_train, 2)
X_test = np.round(X_test, 2)
y_train = np.array(y_train)
y_test = np.array(y_test
)
print(X_train.shape, X_test.shape) # (512, 9) ,(171, 9) 加和正好是683
展示一些数据吧:
print(X_train[0:5])
print('\n')
print(X_test[0:5])
# 前五条
'''
[[-1.19 -0.69 -0.04 -0.62 -0.53 -0.67 -0.56 -0.59 -0.34]
[-1.19 0.31 -0.04 2.55 0.37 1.87 0.69 1.09 -0.34]
[ 0.24 -0.03 -0.72 -0.62 -0.53 -0.67 -0.97 -0.59 -0.34]
[-1.19 -0.69 -0.72 -0.62 -0.53 -0.67 -0.14 -0.59 -0.34]
[-1.19 -0.69 -0.72 -0.62 -0.53 -0.67 -0.14 -0.59 -0.34]]
[[ 0.24 0.31 0.65 -0.62 2.18 -0.67 -0.14 1.09 -0.34]
[-0.47 -0.69 -0.72 -0.62 -0.53 -0.67 -0.56 -0.59 -0.34]
[ 2.04 1.63 1.67 -0.27 2.18 1.87 0.27 1.77 4.97]
[-0.12 1.63 0.99 0.44 -0.08 0.18 2.76 1.09 -0.34]
[ 0.24 -0.36 0.3 -0.62 -0.98 -0.67 -0.97 -0.59 -0.34]]
'''
你要知道我们的目的就是找到w和b,能够让我们的训练集误差最小,而我们的数据集特征维度是:dim = 9,所以w长度就是9
2)正向传播
我们先初始化一个w和b
def initialize_with_zeros(dim):
w = np.zeros((dim,1))
b = 0
return w,b
# 这里dim = 9
'''
[[0.]
[0.]
[0.]
[0.]
[0.]
[0.]
[0.]
[0.]
[0.]]
'''
定义激励函数:
def sigmoid(z):
a = 1/(1+np.exp(-z))
return a
正向传播:
# 这里的X就是我们的训练集,只是形状为:(dim, 512),也就是X_train进行了转置 # 因为机器学习领域,我们所指的向量都是列向量 # X_train.shape = (512, 9),转置后为(9 , 512),每一列就是一个样本的特征向量值 w, b = initialize_with_zeros(9) X = X_train.T A = sigmoid(np.dot(w.T,X)+b) print(A.shape) # (1, 512),得到这个向量,表示每个样本的wx + b的值经过激活函数 print(A) # 因为初始化w的9个分量都是0,所以激活前值为0,经过激活函数得到0.5

其实这就是逻辑回归的第二个假设:假设该样本为正的概率:
\( P(y=1|x;\theta ) = \frac{1}{1+e^{-z}} = \frac{1}{1+e^{-\theta^Tx}} \)
损失:(该轮所有训练样本的平均损失:也就是上面的负对数损失函数)
m = X.shape[1] # 样本数目 Y = y_train cost = -( np.sum( Y*np.log(A) + (1-Y)*np.log(1-A) ) ) / m cost ''' 0.6931471805599453 '''
有了该轮的损失,下面我们就是想法通过调整权重w和偏置b,重新计算cost,使得cost能够降低(比当前cost:0.69小)
3)极大似然函数
上面我们也说过:逻辑回归的损失函数是它的极大似然函数(没毛病吧,老铁!我们只需要求一个最佳的参数w,能够使得所有样本的概率值之积最大)
可是这么多样本,概率都在0-1之间,相乘后的结果值会很小很小,所以才会取对数,求最大值(梯度下降来求最小值,所以我们可以对目标函数取负值,然后求新的目标函数最小值,就可以使用梯度下降啦)
我们可以参考上面的推导过程:我这里画了一个图,对与一个样本的梯度和所有样本的梯度计算以及如何更新一个权重$w_1$,到如何更新9个权重$w_9$,这里的512是训练样本数量,共9个特征值
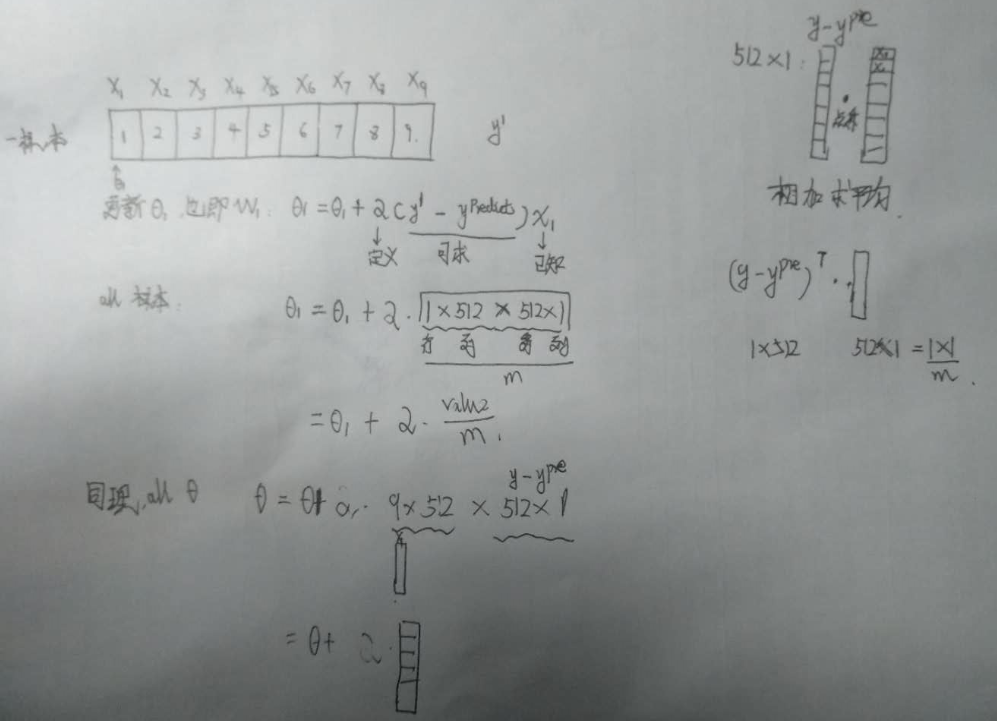
自己计算可以一个样本一个样本来,程序可以利用矩阵运算一下子求出dw和db:
def propagate(w, b, X, Y):
"""
传参:
w -- 权重, shape: (dim, 1)
b -- 偏置项, 一个标量
X -- 数据集,shape: (dim, m),m为样本数
Y -- 真实标签,shape: (1,m)
返回值:
cost, dw ,db,后两者放在一个字典grads里
"""
#获取样本数m:
m = X.shape[1]
# 前向传播 :
A = sigmoid(np.dot(w.T,X)+b) # 调用前面写的sigmoid函数
cost = -(np.sum(Y*np.log(A)+(1-Y)*np.log(1-A)))/m
# 反向传播:
dZ = A-Y
dw = (np.dot(X,dZ.T)) / m
db = (np.sum(dZ)) / m
#返回值:
grads = {"dw": dw,
"db": db}
return grads, cost
有了梯度,我们再根据学习率,来求出每次的步长,来进行梯度上升或者下降(上升或者下降取决于你对损失函数是否添加了符号)
然后我们经过多轮训练,反复调整权重$w$:
def optimize(w, b, X, Y, num_iterations, learning_rate, print_cost = False):
#定义一个costs数组,存放每若干次迭代后的cost,从而可以画图看看cost的变化趋势:
costs = []
#进行迭代:
for i in range(num_iterations):
# 用propagate计算出每次迭代后的cost和梯度:
grads, cost = propagate(w,b,X,Y)
dw = grads["dw"]
db = grads["db"]
# 用上面得到的梯度来更新参数:
w = w - learning_rate*dw
b = b - learning_rate*db
# 每100次迭代,保存一个cost看看:
if i % 100 == 0:
costs.append(cost)
# 这个可以不在意,我们可以每100次把cost打印出来看看,从而随时掌握模型的进展:
if print_cost and i % 100 == 0:
print ("Cost after iteration %i: %f" %(i, cost))
#迭代完毕,将最终的各个参数放进字典,并返回:
params = {"w": w,
"b": b}
grads = {"dw": dw,
"db": db}
return params, grads, costs
最后我们就可以根据训练结果来进行预测啦:
def predict(w,b,X):
m = X.shape[1]
Y_prediction = np.zeros((1,m))
A = sigmoid(np.dot(w.T,X)+b)
for i in range(m):
if A[0,i]>0.5:
Y_prediction[0,i] = 1
else:
Y_prediction[0,i] = 0
return Y_prediction
def logistic_model(X_train,Y_train,X_test,Y_test,learning_rate=0.1,num_iterations=2000,print_cost=False):
#获特征维度,初始化参数:
dim = X_train.shape[1]
W,b = initialize_with_zeros(dim)
#梯度下降,迭代求出模型参数:
params,grads,costs = optimize(W,b,X_train.T,Y_train,num_iterations,learning_rate,print_cost)
W = params['w']
b = params['b']
#用学得的参数进行预测:
prediction_train = predict(W,b,X_train.T)
prediction_test = predict(W,b,X_test.T)
#计算准确率,分别在训练集和测试集上:
accuracy_train = 1 - np.mean(np.abs(prediction_train - Y_train))
accuracy_test = 1 - np.mean(np.abs(prediction_test - Y_test))
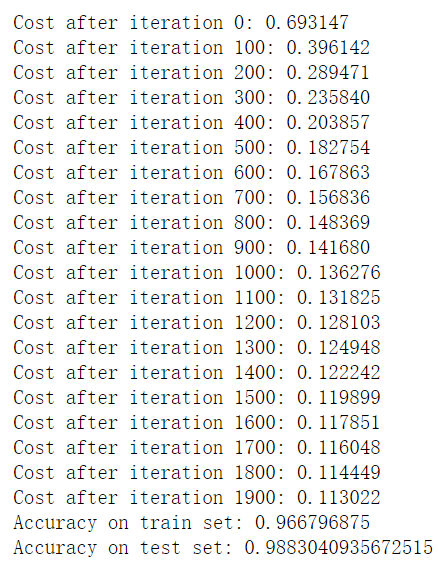
print("Accuracy on train set:",accuracy_train )
print("Accuracy on test set:",accuracy_test )
#为了便于分析和检查,我们把得到的所有参数、超参数都存进一个字典返回出来:
d = {"costs": costs,
"Y_prediction_test": prediction_test ,
"Y_prediction_train" : prediction_train ,
"w" : w,
"b" : b,
"learning_rate" : learning_rate,
"num_iterations": num_iterations,
"train_acy":accuracy_train,
"test_acy":accuracy_test
}
return d
d = logistic_model(X_train, np.array(y_train), X_test, np.array(y_test), learning_rate = 0.005, num_iterations = 2000, print_cost = True)
这里矩阵运算注意来回转置,其实不必去注意这种转换,个人觉得没有必要去扣这种细节,反正原矩阵相乘不行,那就转置相乘,就到这里吧