数据归一化

（什么~为什么~哪些）

一、为何需要归一化

　不同的评价指标往往具有不同的量纲（例如：对于评价房价来说量纲指：面积、房价数、楼层等；对于预测某个人患病率来说量纲指：身高、体重等）

　这样的情况会影响到数据分析的结果，为了消除指标之间量纲的影响，需要进行数据标准化处理，以解决数据指标之间的可比性。原始数据经过数据标准化处理后，各指标处于同一数量级，适合进行综合对比评价

　　（1）归一化后加快了梯度下降求最优解的速度

　　（2）归一化有可能提高精度（归一化是让不同维度之间的特征在数值上有一定的比较性）

二、例子讲解

　假定为了预测房子价格，自变量为面积，房间数两个，因变量为房价，那么可以得到的公式为：\(y = \theta_1x_1 + \theta_2x_2\)，其中x₁代表房间数，x₂代表面积，首先给出两张图代表数据是否均一化的最优解寻解过程

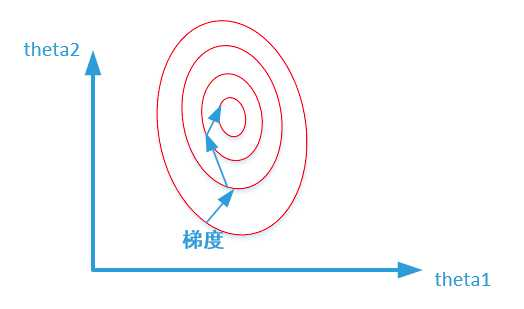
　未归一化：

　归一化之后：

 

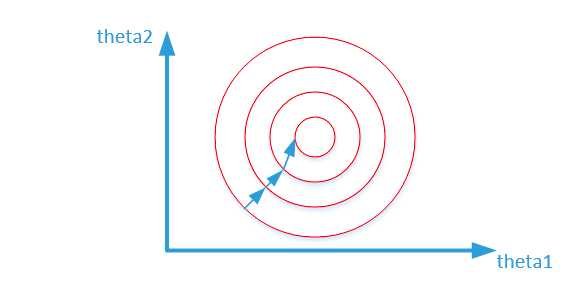
　寻找最优解也就是寻找使得损失函数值最小的theta1、theta2。上述两幅图代表的是损失函数的等高线。当数据没有归一化的时候，面积数的范围可以从0-1000，房间数的范围一般为0-10，可以看出面积数的取值范围远大于房间数

　形成的影响就是在形成损失函数的时候，数据没有归一化的表达式可以为：\(J = (3\theta_1 + 600\theta_2 - y)^2\)，造成图像的等高线为类似的椭圆形状，最优解的寻优过程如下图所示：

　而数据归一化后，损失函数的表达式可以表示为：\(J = (0.5\theta_1 + 0.55\theta_2 - y)^2\)，其中变量的前面系数都在【0-1】范围之间，则图像的等高线为类似的圆形形状，最优解的寻优过程如下图所示:

　

　从上面可以看出，数据归一化后，最优解的寻优过程明显会变得平缓，更容易正确的收敛到最优解

 

三、两种常用的归一化方法：

　1）min-max标准化（Min-Max Normalization）（线性函数归一化）：

• • 　定义：也称为离差标准化，是对原始数据的线性变换，使得结果映射到0-1之间
  • 　本质：把数变为【0,1】之间的小数
  • 　转换函数：\((X - Min)/(Max - Min)\)

　其中：Max为样本数据的最大值，Min为样本数据的最小值。缺陷：当有新数据加入时，可导致Max和Min的变化，需要重新定义

 

　2）0均值标准化（Z-score standardlization）

• • 　定义：这种方法给与原始数据的均值（mean）和标准差（standard deviation）进行数据的标准化。经过处理的数据符合标准正态分布，即均值为0，标准差为1
  • 　本质：把有量纲表达式变成无量纲表达式
  • 　转换函数：\((X - \mu)/\delta\)

　其中，\(\mu\)为所有样本数据的均值。\(\delta\)为所有样本数据的标准差

 

四、sklearn模块中的归一化

　数据正规化（data normalization）是将数据的每个样本（向量）变换为单位范数的向量，各样本之间是相互独立的．其实际上，是对向量中的每个分量值除以正规化因子．常用的正规化因子有 L1, L2 和 Max

 

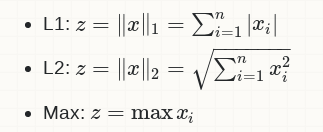
import numpy as np
from sklearn.preprocessing import normalize

x = np.array([[1, 2, 3, 4], [3,4,5,6], [5,6,7,8]], dtype='float32')
print("Before normalization:\n ", x, '\n')

options = ['l1', 'l2', 'max']
for opt in options:
    norm_x = normalize(x, axis=0,  norm=opt)
    print("After %s normalization:\n" % opt.capitalize(), norm_x, '\n')

　　结果如下：