GBDT
核心~结合(易少缺过)~最佳~步骤
一、决策树分类
决策树分为两大类,分类树和回归树
分类树用于分类标签值,如晴天/阴天/雾/雨、用户性别、网页是否是垃圾页面
回归树用于预测实数值,如明天的温度、用户的年龄
两者的区别:
- 分类树的结果不能进行加减运算,晴天+晴天没有实际意义
- 回归树的结果是预测一个数值,可以进行加减运算,例如 20 岁+3 岁=23 岁
- GBDT中的决策树是回归树,预测结果是一个数值,在点击率预测方面常用 GBDT,例如用户点击某个内容的概率
二、GBDT
GBDT 的全称是 Gradient Boosting Decision Tree,梯度提升决策树,核心在于累加所有树的结果作为最终结果,因此决定了他用的决策树是回归树
为什么梯度提升方法倾向于选择决策树作为基学习器呢?(也就是 GB 为什么要和 DT 结合)
决策树是 if-then 规则的集合,易于理解,预测速度快。
决策树算法相比于其他的算法需要更少的特征工程,比如可以不用做特征标准化
决策树可以很好的处理字段缺失的数据,也可以不用关心特征间是否相互依赖等
不过,单独使用决策树算法时,容易过拟合。但通过各种方法,抑制决策树的复杂性,降低单颗决策树的拟合能力,再通过梯度提升的方法集成多个决策树,最终能够很好的解决过拟合的问题
由此可见,梯度提升方法和决策树学习算法可以互相取长补短,是一对完美的搭档
至于抑制单颗决策树的复杂度的方法有很多,比如限制树的最大深度、限制叶子节点的最少样本数量、限制节点分裂时的最少样本数量、吸收 bagging 的思想对训练样本采样(subsample)
在学习单颗决策树时只使用一部分训练样本、借鉴随机森林的思路在学习单颗决策树时只采样一部分特征、在目标函数中添加正则项惩罚复杂的树结构等
GBDT的思想可以用一个通俗的例子解释,假如有个人30岁,我们首先用20岁去拟合,发现损失有10岁,这时我们用6岁去拟合剩下的损失,发现差距还有4 岁,第三轮我们用3岁拟合剩下的差距,差距就只有一岁了
三、简单讲解GBDT
GBDT的核心就在于,每一棵树学的是之前所有树结论和的残差。比如A的真实年龄是18岁,但第一棵树的预测年龄是12岁,差了6岁,即残差为6岁
那么在第二棵树里我们把A的年龄设为6岁去学习,如果第二棵树真的能把A分到6岁的叶子节点,那累加两棵树的结论就是A的真实年龄;如果第二棵树的结论是5岁,则A仍然存在1岁的残差,第三棵树里A的年龄就变成1岁,继续学
这就是Gradient Boosting在GBDT中的意义
年龄预测为例,简单起见训练集只有4个人,A,B,C,D,年龄分别是14,16,24,26。其中A,B分别是高一和高三学生;C,D分别是应届毕业生和工作两年的员工。
如果用一棵传统的回归决策树来训练,会得到如下图1所示结果:
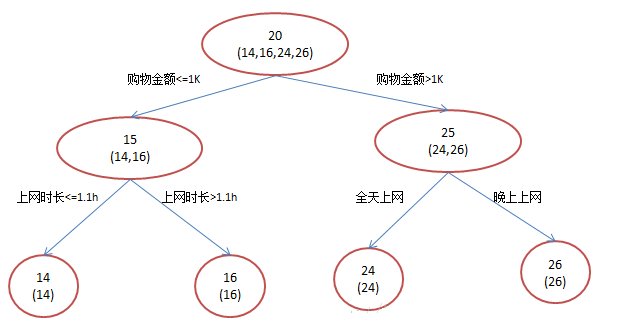
使用GBDT,由于数据太少,我们限定叶子节点最多有两个,即每棵树都只有一个分枝,并且限定只学两棵树。我们会得到如下图2所示结果:
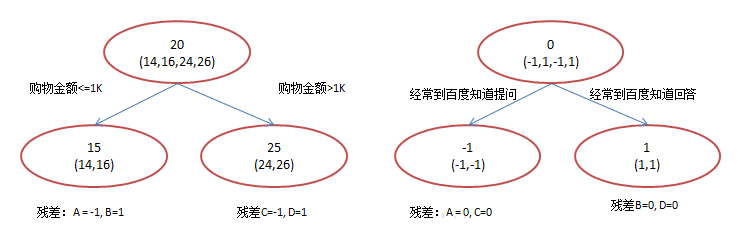
在第一棵树分枝和图1一样,由于A,B年龄较为相近,C,D年龄较为相近,他们被分为两组,每组用平均年龄作为预测值。此时计算残差(残差的意思就是: A的预测值 + A的残差 = A的实际值),所以A的残差就是14 - 15 = -1
注意,A的预测值是指前面所有树累加的和,这里前面只有一棵树所以直接是15,如果还有树则需要都累加起来作为A的预测值
进而得到A,B,C,D的残差分别为-1,1,-1,1。然后拿残差替代A,B,C,D的原值,到第二棵树去学习,如果我们的预测值和它们的残差相等,则只需把第二棵树的结论累加到第一棵树上就能得到真实年龄了
这里的数据显然是我刻意做的,第二棵树只有两个值1和-1,直接分成两个节点。此时所有人的残差都是0,即每个人都得到了真实的预测值
换句话说,现在A,B,C,D的预测值都和真实年龄一致了:
A: 14岁高一学生,购物较少,经常问学长问题;预测年龄A = 15 – 1 = 14
B: 16岁高三学生;购物较少,经常被学弟问问题;预测年龄B = 15 + 1 = 16
C: 24岁应届毕业生;购物较多,经常问师兄问题;预测年龄C = 25 – 1 = 24
D: 26岁工作两年员工;购物较多,经常被师弟问问题;预测年龄D = 25 + 1 = 26
那么哪里体现了Gradient呢?其实回到第一棵树结束时想一想,无论此时的cost function是什么,是均方差还是均差,只要它以误差作为衡量标准,残差向量(-1, 1, -1, 1)都是它的全局最优方向,这就是Gradient
四、算法思想
对于回归树算法来说最主要的是寻找最佳的划分点,那么回归树中的可划分点包含了所有特征的所有可取的值。在分类树中最佳划分点的判别标准是熵或者基尼系数,都是用纯度来衡量的
但是在回归树中的样本标签也是连续数值,所以再使用熵之类的指标不再合适,取而代之的是平方误差,它能很好的评判数据分散程度
我们希望最佳划分节点能够使得划分得到的两组数据组内的标签值相近,如果每组的方差都很小,这就说明每组的组内相似度很高,确实应该被划分
下面看看李航《统计学习方法》回归树伪代码:

从上图可以看出:利用方差寻找最佳划分点,预测值选择决策树的叶子节点中所有样本的真实值的均值。
负梯度-残差
GBDT无疑也是Boosting家族的一员,而Adaboost在Boosting家族很出名,但是GBDT并没有采用Adaboost算法!!!那GBDT中的Boosting是怎么做的呢?
先来个通俗理解:假如有个人30岁,我们首先用20岁去拟合,发现损失有10岁,这时我们用6岁去拟合剩下的损失,发现差距还有4岁,第三轮我们用3岁拟合剩下的差距,差距就只有一岁了。如果我们的迭代轮数还没有完,可以继续迭代下面,每一轮迭代,拟合的岁数误差都会减小。
公式表达:在GBDT的迭代中,假设前一轮迭代得到的强学习器是\(f_{t-1}(x)\),损失函数是\(L(y,f_{t-1}(x))\),我们本轮迭代的目标是找到一个CART回归树模型的弱学习器\(f_t(x)\),让本轮的损失函数\(L(y,f_t(x)) = L(y,f_{t-1}(x)+f_t(x))\)最小
GBDT选取了相对来说容易优化的损失函数——平方损失。GBDT使用的平方损失,经过负梯度拟合得到了\(y-f(x_i)\),这就是我们最终要去拟合的,它的另一个名字叫作残差

算法流程
1.初始化弱分类器:
\(f_0(x) = argmin_\gamma\sum_{i=1}^{N}L(y_i,\gamma)\)
2.对迭代轮数有:\(m = 1,2,...,M\)
a.对每个样本\(i = 1,2,...,N\)计算负梯度,即残差 :
\(\gamma_{im} = -\begin{bmatrix}\partial L(y_i,f(x_i))/ \partial f(x_i)\end{bmatrix}_{f(x) = f_{m-1}(x)}\)
b.将上步得到的残差作为样本新的真实值,并将数据\((x_i,\gamma_{im})(i=1,2,...,N)\)作为下棵树的训练数据,得到一颗新的回归树\(f_m(x)\),其对应的叶子节点区域为\(R_{jm},j=1,2,...,J\),其中J为回归树t的叶子节点的个数
c.对叶子区域\(j=1,2,...,J\)计算最佳拟合值:
\(\gamma_{jm} = argmin_\gamma\sum_{x_i\epsilon R_{jm}}L(y_i, f_{m-1}(x_i) + \gamma)\)
d.更新强学习器:
\(f_m(x) = f_{m-1}(x) + \sum_{j=1}^{J}\gamma_{jm}I(x\epsilon R_{jm})\)
3.得到强学习器:
\(f(x) = f_m(x) = f_0(x) + \sum_{m=1}^{M}\sum_{j=1}^{J}\gamma_{jm}I(x\epsilon R_{jm})\)
五、跟着算法来看一个实例
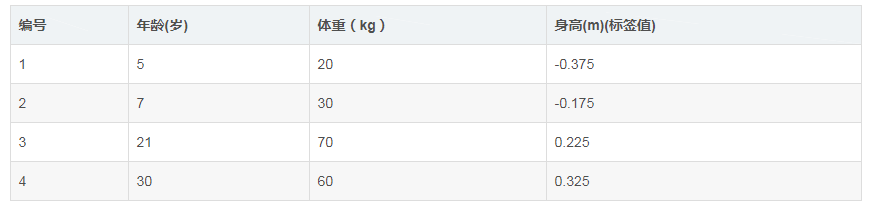
如下表所示:一组数据,特征为年龄、体重,身高为标签值。共有5条数据,前四条为训练样本,最后一条为要预测的样本
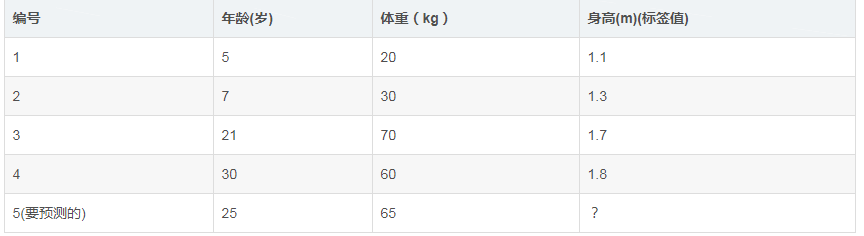
1.初始化弱学习器:\(f_0(x) = argmin_\gamma\sum_{i=1}^{N}L(y_i,\gamma)\)
由于此时只有根节点,样本1,2,3,4都在根节点,此时要找到使得平方损失函数最小的参数\(\gamma\),怎么求呢?平方损失显然是一个凸函数,直接求导,倒数等于零,得到\(\gamma\):
\(\sum_{i=1}^{N}\partial L(y_i,\gamma)/\partial \gamma = \sum_{i=1}^{N}\partial (y_i-\gamma)^2/\partial \gamma = 2(y_1 - \gamma) + 2(y_2 - \gamma) + 2(y_3 - \gamma) + 2(y_4 - \gamma) = 0\)
所以初始化时,\(\gamma\)取值为所有训练样本标签值的均值。\(\gamma = (1.1 + 1.3 + 1.7 + 1.8) / 4 = 1.475 \),此时得到初始学习器:\(f_0(x) = \gamma = 1.475\)
2.对迭代轮数\(m=1\):
a.对每个样本\(i = 1,2,...,N\)计算负梯度,即残差 :
\(\gamma_{i1} = -\begin{bmatrix}\partial L(y_i,f(x_i))/ \partial f(x_i)\end{bmatrix}_{f(x) = f_0(x)}\)
说白了,就是残差(上面已经解释过了),在此例中,残差在下表列出:
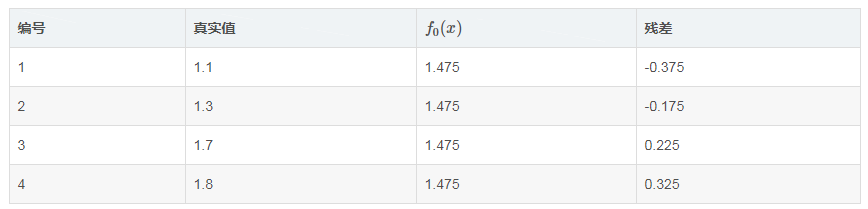
b.将上步得到的残差作为样本新的真实值,并将数据\((x_i,\gamma_{im})(i=1,2,...,N)\)作为下棵树的训练数据,得到一颗新的回归树\(f_1(x)\),其对应的叶子节点区域为\(R_{j1},j=1,2,...,J\),其中J为回归树t的叶子节点的个数(这里J=2)
接着,寻找回归树的最佳划分节点,遍历每个特征的每个可能取值。从年龄特征的5开始,到体重特征的70结束,分别计算方差,找到使方差最小的那个划分节点即为最佳划分节点。
例如:以年龄7为划分节点,将小于7的样本划分为一类,大于等于7的样本划分为另一类。样本1为一组,样本2,3,4为一组,两组的方差分别为0,0.047,两组方差之和为0.047。所有可能划分情况如下表所示
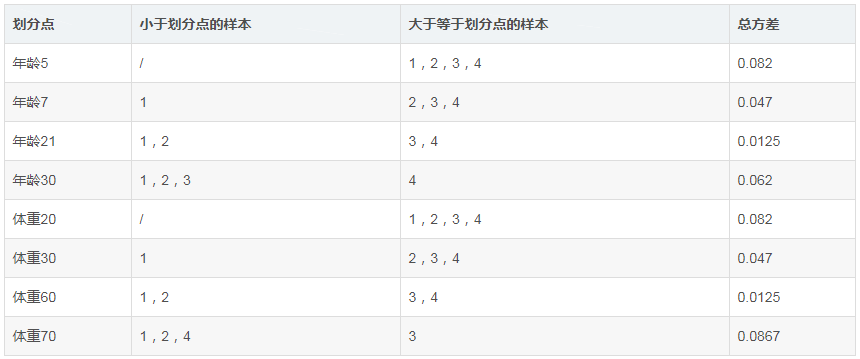
以上划分点是的总方差最小为0.0125有两个划分点:年龄21和体重60,所以随机选一个作为划分点,这里我们选年龄21。 此时还需要做一件事情,给这两个叶子节点分别赋一个参数,来拟合残差。
c.对叶子区域\(j=1,2,...,J\)计算最佳拟合值:
\(\gamma_{j1} = argmin_\gamma\sum_{x_i\epsilon R_{j1}}L(y_i, f_0(x_i) + \gamma)\)
这里其实和上面初始化学习器是一个道理,平方损失,求导,令导数等于零,化简之后得到每个叶子节点的参数\(\gamma\),其实就是标签值的均值。 根据上述划分节点:
样本1,2为左叶子节点,\((x_1,x_2 \epsilon R_{11})\),所以\(\gamma_{11} = (-0.375 - 0.175) / 2 = -0.275\)
样本3,4为右叶子节点,\((x_3,x_4 \epsilon R_{21})\),所以\(\gamma_{21} = (0.225 + 0.325) / 2 = 0.275\)
d.更新强学习器:
\(f_1(x) = f_0(x) + \sum_{j=1}^{2}\gamma_{j1}I(x\epsilon R_{j1})\)
此时可以获得每个样本在下轮循环M=2时的值,即将得到的残差作为样本新的真实值,参与到下一颗回归树的构建,如下:

3.对迭代轮数\(m = 1,2,...,M\),循环迭代M次,M是人为控制的参数,迭代结束生成M棵树
4.得到最后的强学习器:
为了方别展示和理解,我们假设M=1,根据上述结果得到强学习器:
\(f(x) = f_m(x) = f_0(x) + \sum_{m=1}^{M}\sum_{j=1}^{J}\gamma_{jm}I(x\epsilon R{jm}) = f_0(x) + \sum_{j=1}^{2}\gamma_{j1}(x\epsilon R_{j1})\)
如图所示得到只迭代一次,只有一颗树的GBDT:

5.预测样本5:
样本5在根节点中(即初始学习器)被预测为1.475,样本5的年龄为25,大于划分节点21岁,所以被分到了右边的叶子节点,同时被预测为0.275。此时便得到样本5的最总预测值为1.75。
六、小结
既然图1和图2 最终效果相同,为何还需要GBDT呢?答案是过拟合。我们发现图1为了达到100%精度使用了3个feature(上网时长、时段、网购金额)相对来说图2的boosting虽然用了两棵树 ,但其实只用了2个feature就搞定
GBDT几乎可用于所有回归问题(线性/非线性),相对logistic regression仅能用于线性回归,GBDT的适用面非常广。亦可用于二分类问题(设定阈值,大于阈值为正例,反之为负例)
七、参考文献
李航 《统计学习方法》
博客:https://blog.csdn.net/zpalyq110/article/details/79527653



