层次聚类

一、Hierarchical Clustering简介

　层次聚类(Hierarchical Clustering)是聚类算法的一种，通过计算不同类别数据点间的相似度来创建一棵有层次的嵌套聚类树。在聚类树中，不同类别的原始数据点是树的最低层，树的顶层是一个聚类的根节点。

二、层次聚类的合并算法

　假设有N个待聚类的样本，合并的步骤：

1. 初始化：每个样本归为一类，并计算每个类之间的距离
2. 寻找距离最近的两个类，合并为一个类
3. 重新计算合并后的类和其他类之间的距离
4. 重复2和3，直至所有样本都划分到某一类

　其中求各个类之间的距离，即为求各个类之间的相似度，相似度的求法：

1. SingleLinkage-取两类中距离最近的两个样本的距离作为两类的距离
2. CompleteLinkage-取两类中距离最远的两个样本的距离作为两类的距离
3. AverageLinkage-把两类中的样本两两的距离全部放在一起求一个平均值，作为两类的距离

 

三、以欧式距离计算方法为例，讲解层次聚类过程

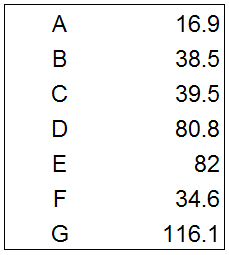
　a) A-G样本数据如下：

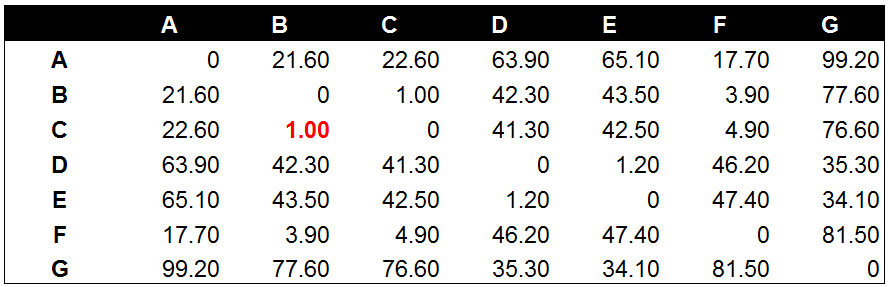
　b) 创建欧式距离矩阵：两两计算距离，其中A—>B表示数据点A到数据点B的距离，B—>A则代表数据点B到数据点A的距离。这两个距离值是相同的，因此欧式距离矩阵呈对角线对称（绿色部分和蓝色部分）。其中对角线的0值是数据点与自己的距离值。将所有数据点间的距离结果进行对比，选择其中距离最近的两个数据点进行组合，并迭代这一过程：

　c) 经过计算数据点B和数据点C与其他数据点相比有最高的相似度。因此，B和C进行组合。并再次计算其他数据点间的距离：

 

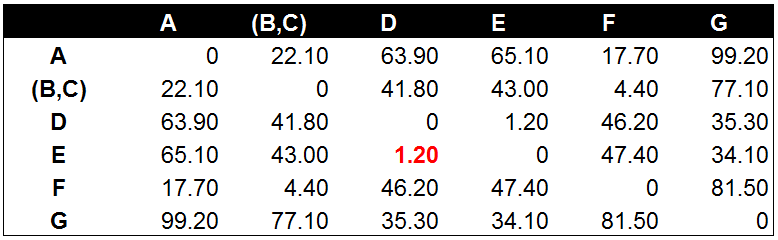
　d) 数据点D到数据点E的距离在所有的距离值中最小，为1.20。这表示在当前的所有数据点中（包含组合数据点），D和E的相似度最高。将数据点D和数据点E进行组合。并再次计算其他数据点间的距离:

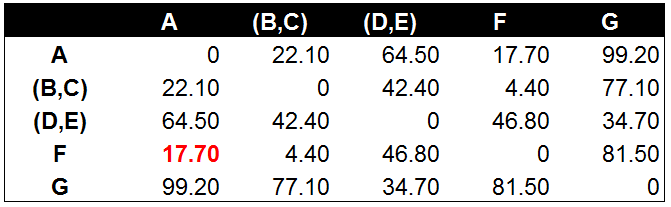
　e) 从上面计算看出，A和F最近，合并AF：

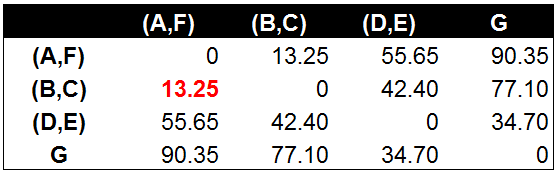
　f) 从上面计算看出，(A,F)和(B,C)最近，合并AF和BC：

 

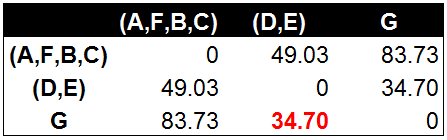
　g) 从上面计算看出，G和(D,E)最近，合并G和(D,E)，这也是聚类树的最顶层的两个数据点。

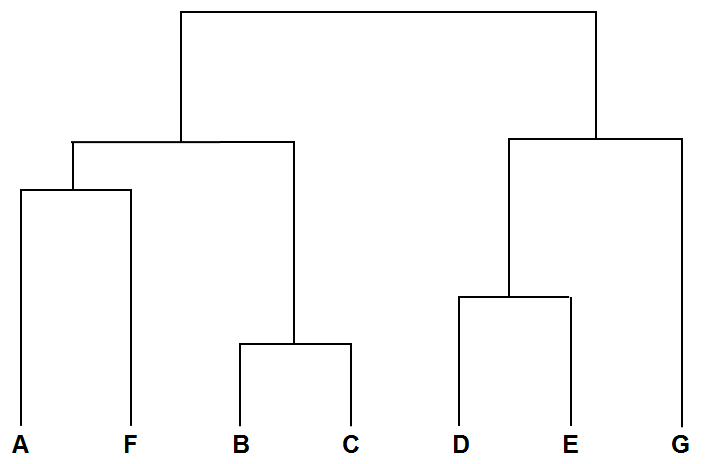
　h) 层次聚类树状图：