数据降维

一、PCA：(principal component analysis)

　　1、为何需要PCA

• 比如拿到一个汽车的样本，里面既有以“千米/每小时”度量的最大速度特征，也有“英里/小时”的最大速度特征，显然这两个特征有一个多余。
• 拿到一个样本，特征非常多，而样例特别少，这样用回归去直接拟合非常困难，容易过度拟合。比如北京的房价：假设房子的特征是（大小、位置、朝向、是否学区房、建造年代、是否二手、层数、所在层数），搞了这么多特征，结果只有不到十个房子的样例。要拟合房子特征‐>房价的这么多特征，就会造成过度拟合。

　　2、PCA 的思想

　　　　将 n维特征映射到 k 维上（k<n） ，这 k 维是全新的特征，称为主元，是重新构造出来的 k 维特征，而不是简单地从 n 维特征中去除其余 n‐k 维特征

　　3、实例讲解过程

　　

x	y
2.5	2.4
0.5	0.7
2.2	2.9
1.9	2.2
3.1	3.0
2.3	2.7
2	1.6
1	1.1
1.5	1.6
1.1	0.9

　　　　假设我们有2 维数据，行代表样例，列代表特征，这里有 10 个样例，每个样例两个特征

　　step1：求每个特征的均值，然后对于所有的样例，都减去对应的均值。这里 x 的均值是 1.81，y 的均值是 1.91，减去后得到

 

x-average(x)	y-average(y)
0.69	0.49
-1.31	-1.21
0.39	0.99
0.09	0.29
1.29	1.09
0.49	0.79
0.19	-0.31
-0.81	-0.81
-0.31	-0.31
-0.71	-1.01

 　　step2：求协方差矩阵，如果数据是 3 维，那么协方差矩阵是

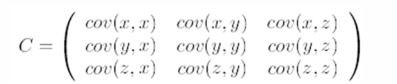　　　其中协方差公式为：

　　　

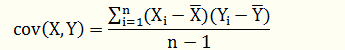
　　注：对角线上分别是 x 和 y 的方差，非对角线上是协方差。

　　　　l  协方差 > 0时，表示 x 和 y 若有一个增，另一个也增；

　　　　l  协方差 < 0时，表示一个增，一个减；

　　　　l  协方差 = 0 时，两者独立。

　　　　l  协方差绝对值越大，两者对彼此的影响越大，反之越小。

 　　4.代码实例：

from sklearn.decomposition import PCA
import numpy as np
pca = PCA(n_components=2)
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])  
pca.fit(X)
print(pca.explained_variance_ratio_)

 　　还需要研究