聚类算法

一、DBSCAN

　1.简介：

　　DBSCAN（Density-Based Spatial Clustering of Applications with Noise，具有噪声的基于密度的聚类方法）是一种基于密度的空间聚类算法。

　　该算法要求聚类空间中的一定区域内所包含对象（点或其他空间对象）的数目不小于某一给定阈值。

　　DBSCAN算法的显著优点是聚类速度快且能够有效处理噪声点和发现任意形状的空间聚类，具有两个比较明显的弱点：

• 当数据量增大时，要求较大的内存支持I/O消耗也很大；
• 当空间聚类的密度不均匀、聚类间距差相差很大时，聚类质量较差

　2.原理：

　　该算法将数据点分为3类：

• 核心点：在半径Eps内含有超过MinPts数目的点
• 边界点：在半径Eps内含有点的数量小于MinPts，但是落在核心点邻域内的点
• 噪音点：既不是核心点又不属于边界点
• 直接密度可达(directly density-reachable)：如果p在q的Eps邻域内，而q是一个核心对象，则从对象q出发到p时是直接密度可达的
  

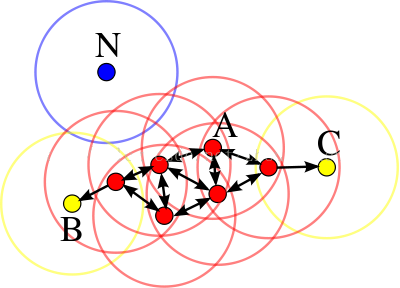
红色为核心点，黄色为边界点，蓝色为噪音点，minPts = 4，Eps是图中圆的半径大小有关

 

　　过程如下：

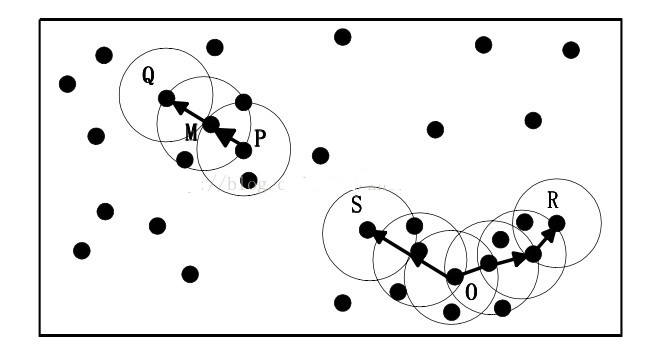　　3. scikit-learn DBSCAN聚类实例

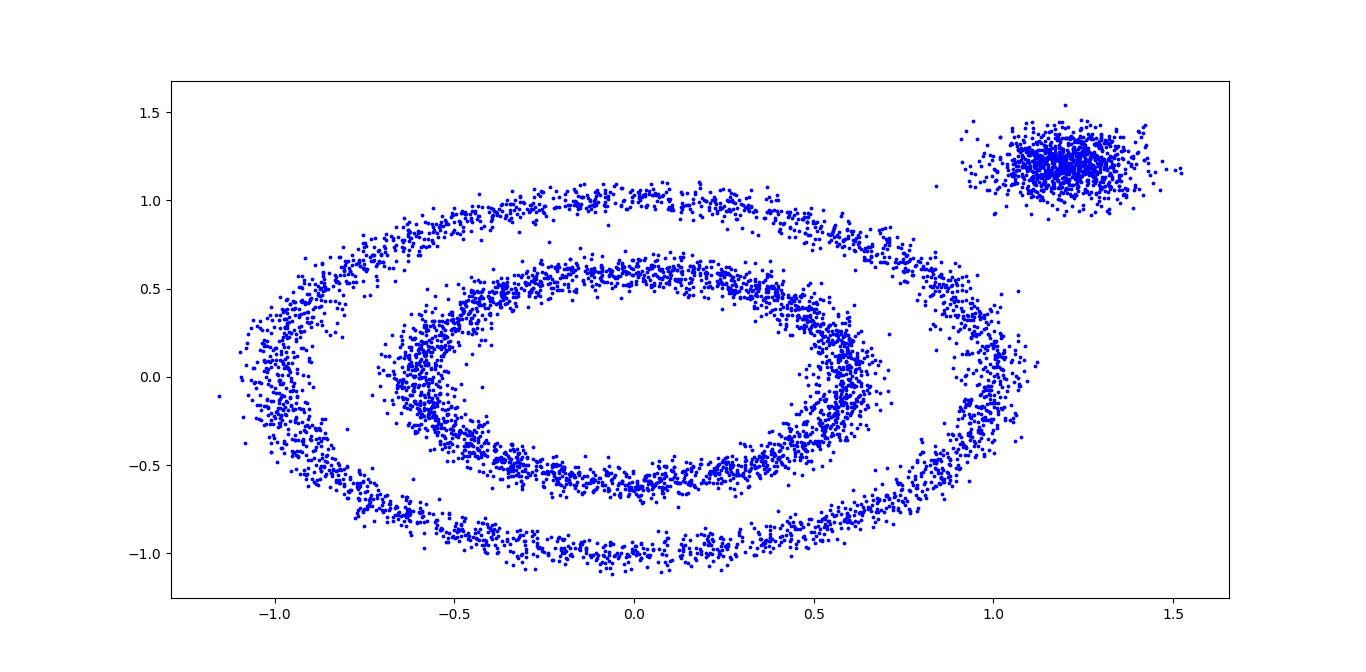
　　　　首先，我们生成一组随机数据，为了体现DBSCAN在非凸数据的聚类优点，我们生成了三簇数据，两组是非凸的。代码如下：

#coding = utf-8
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

#make_circles: Make a large circle containing a smaller circle in 2d.
#factor: Scale factor between inner and outer circle.
X1, y1 = datasets.make_circles(n_samples=5000, factor=0.6,noise=0.05)
print X1.shape
print y1

#make_blobs: Generate isotropic Gaussian blobs for clustering.
#n_features: The number of features for each sample.
#cluster_std: The standard deviation of the clusters.
X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2, 1.2]], cluster_std=[[0.1]],random_state=9)
print X2.shape
print y2

#np.concatenate: 拼接
X = np.concatenate((X1, X2))
print X.shape

#s: marker size
plt.scatter(X[:, 0], X[:, 1], marker='o', s=3, color='blue')
plt.show()

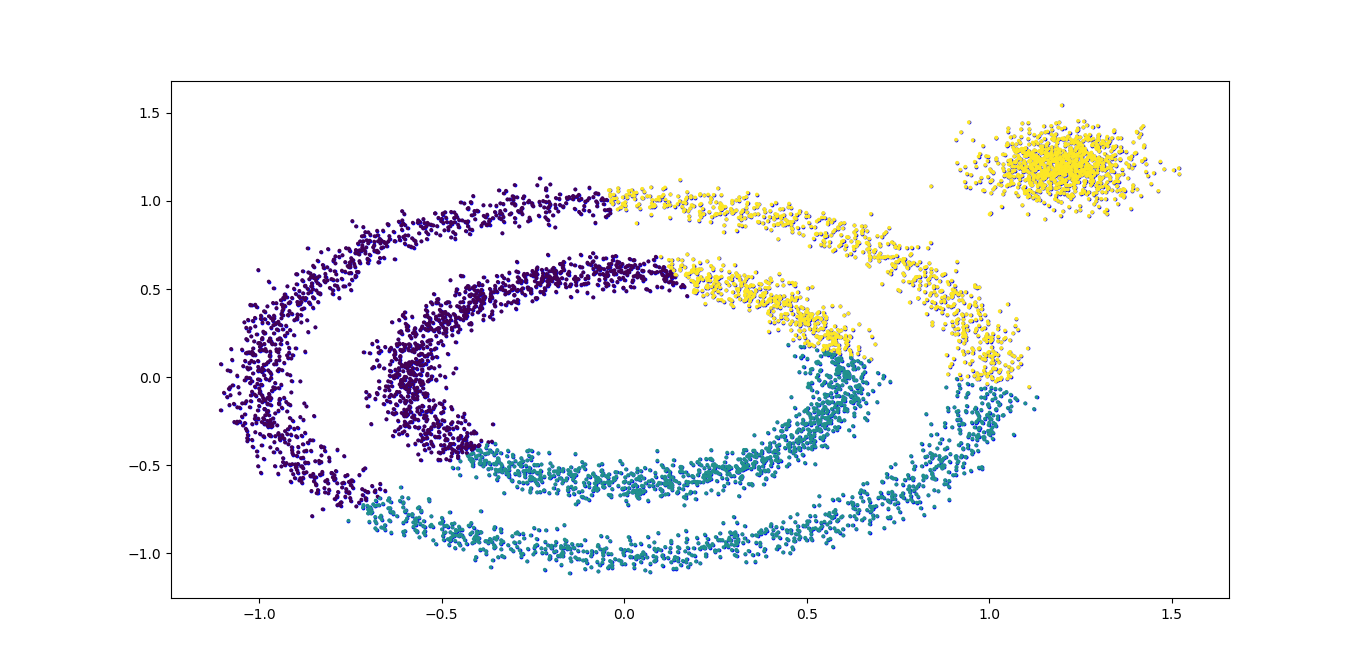
　　K-Means的聚类，代码如下：

#K-Means聚类效果
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3, random_state=9)
y_pred = kmeans.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=3)
plt.show()

　　K-Means对于非凸数据集的聚类表现不好，从上面代码输出的聚类效果图可以明显看出，输出图如下：

　　那么如果使用DBSCAN效果如何呢？我们先不调参，直接用默认参数，代码如下： 

#DBSCAN: 使用默认参数
from sklearn.cluster import DBSCAN
dbscan = DBSCAN()
y_pred = dbscan.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=3)
plt.show()

 　　DBSCAN居然认为所有的数据都是一类，输出效果图如下：

 

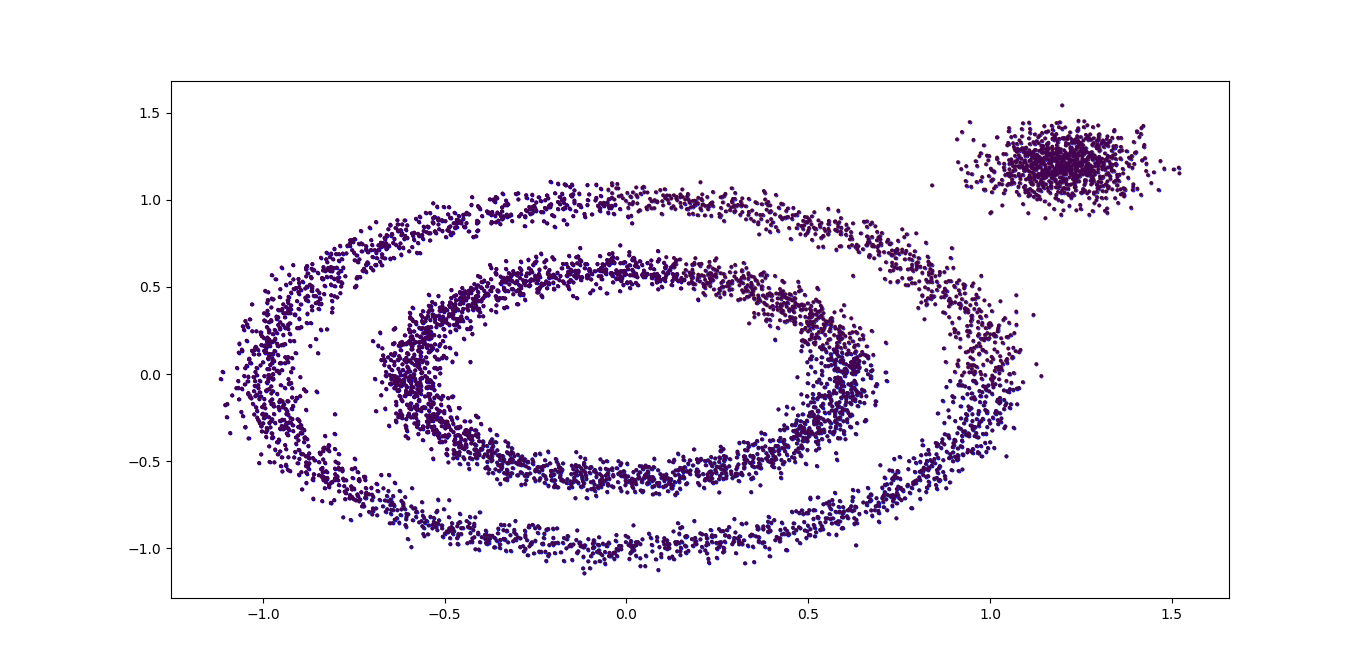
　　我们需要对DBSCAN的两个关键的参数eps和min_samples进行调参, 从上图我们可以发现，类别数太少，我们需要增加类别数，那么我们可以减少邻域的大小，默认是0.5，我们减到0.1看看效果。代码如下：

#DBSCAN: 调参邻域eps
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps = 0.1)
y_pred = dbscan.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=3)
plt.show()

 　　　聚类效果图如下：

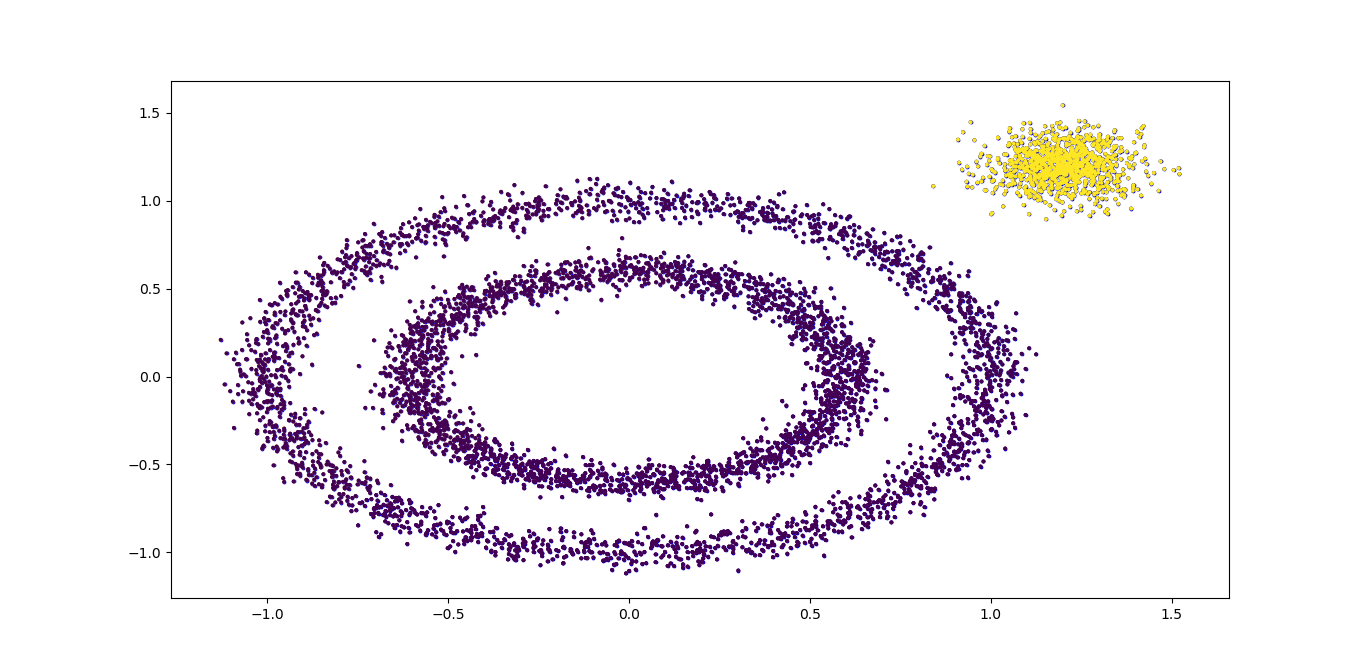
 　　可以看到聚类效果有了改进，边上的那个簇已经被发现出来了。此时我们需要继续调参增加类别，有两个方向都是可以的，一个是继续减少eps，另一个是增加min_samples。将min_samples从默认的5增加到10，代码如下：

#DBSCAN: 调参样本数
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps = 0.1, min_samples = 10)
y_pred = dbscan.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=3)
plt.show()

 　　效果如下：

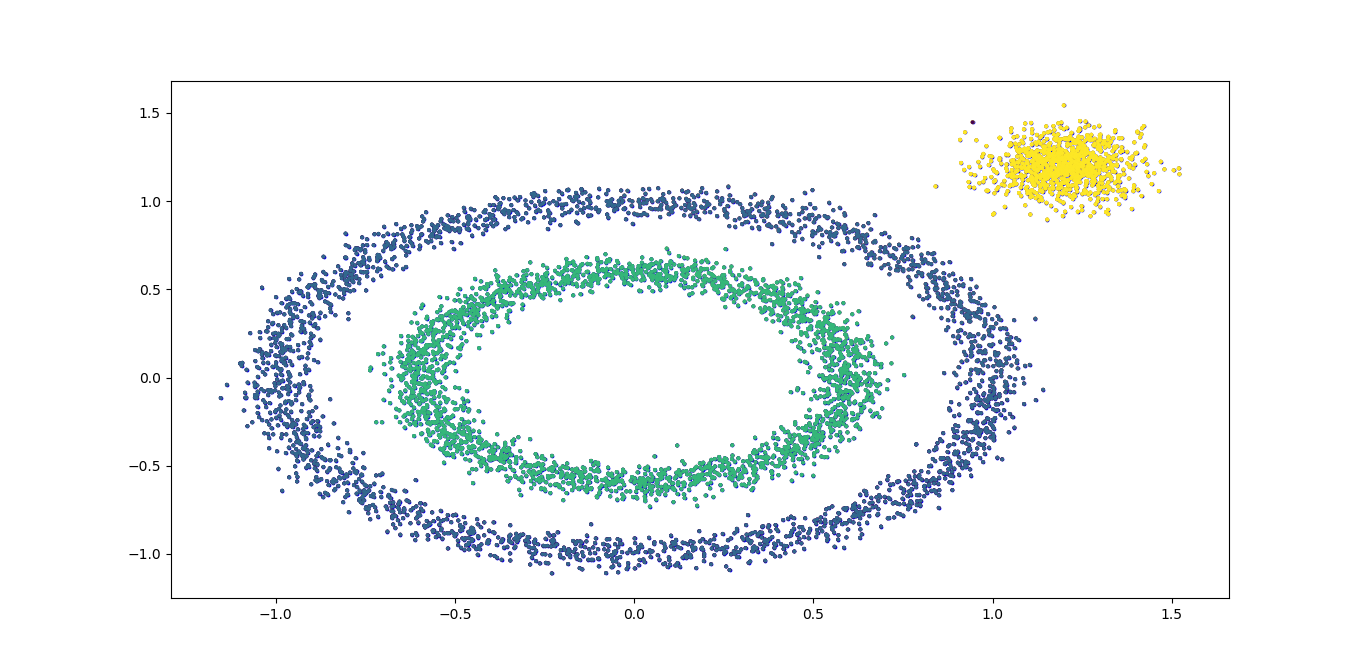　　效果已经不错了，总代码如下：

#coding = utf-8
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

#make_circles: Make a large circle containing a smaller circle in 2d.
#factor: Scale factor between inner and outer circle.
X1, y1 = datasets.make_circles(n_samples=5000, factor=0.6,noise=0.05)
print X1.shape
print y1


#make_blobs: Generate isotropic Gaussian blobs for clustering.
#n_features: The number of features for each sample.
#cluster_std: The standard deviation of the clusters.
X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2, 1.2]], cluster_std=[[0.1]],random_state=9)
print X2.shape
print y2

#np.concatenate: 拼接
X = np.concatenate((X1, X2))
print X.shape

#s: marker size
plt.scatter(X[:, 0], X[:, 1], marker='o', s=3, color='blue')
#plt.show()

#K-Means聚类效果
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3, random_state=9)
y_pred = kmeans.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=3)
#plt.show()

#DBSCAN: 使用默认参数
from sklearn.cluster import DBSCAN
dbscan = DBSCAN()
y_pred = dbscan.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=3)
#plt.show()

#DBSCAN: 调参邻域
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps = 0.1)
y_pred = dbscan.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=3)
#plt.show()

#DBSCAN: 调参样本数
from sklearn.cluster import DBSCAN
dbscan = DBSCAN(eps = 0.1, min_samples = 10)
y_pred = dbscan.fit_predict(X)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=3)
plt.show()

 　　DBSCAN其实需要调参的就是两个参数eps和min_samples，这两个值的组合对最终的聚类效果有很大的影响。