随机森林的原理分析

集成~依赖~单元~投票~拟合~抗噪~生长~袋外

高大并重~噪多

基~串~投~敏~同~方

一、优势互补：

　　RF属于集成学习，集成学习通过构建并结合多个分类器来完成学习任务，常可获得比单一学习器更好的泛化性能

　　一个简单例子：在二分类任务中，假定三个分类器在三个测试样本上的表现如下图，其中√表示分类正确，×表示分类错误，集成学习的结果通过投票法产生，即“少数服从多数”。如下图：

• （a）中，每个分类器都只有66.6%的精度，但集成学习却达到了100%；
• （b）中，三个分类器没有差别，集成之后性能没有提高；
• （c）中，每个分类器的精度都只有33.3%，集成学习的结果变得更糟

　　这个简单地例子显示出：要获得好的集成，个体学习器应“好而不同”，即个体学习器要有一定的“准确性”，即学习器不能太差，并且要有“多样性”，即学习器间具有差异

 

二、集成学习分类

　　根据个体学习器之间的依赖关系，集成学习方法大致可分为两大类：

　　个体学习器之间存在强依赖关系，必须串行生成的序列化方法：代表是Boosting

　　个体学习器间不存在强依赖关系，可同时生成的并行化方法：代表是Bagging和“随机森林”（Random Forest）

 

三、什么是随机森林

　　随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树

　　随机森林的名称中有两个关键词，一个是“随机”，一个就是“森林”。“森林”我们很好理解，一棵叫做树，每棵决策树都是一个分类器（假设现在针对的是分类问题），那么对于一个输入样本，N棵树会有N个分类结果

　　而RF集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出，这就是一种最简单的 Bagging 思想。那么成百上千棵就可以叫做森林了

 

　　举例来说：森林中召开会议，讨论某个动物到底是老鼠还是松鼠，每棵树都要独立地发表自己对这个问题的看法，也就是每棵树都要投票。该动物到底是老鼠还是松鼠，要依据投票情况来确定，获得票数最多的类别就是森林的分类结果。森林中的每棵树都是独立的。

　　森林好理解，那么如何理解随机呢？两个随机

• 随机有放回的抽样：如果不随机有放回抽样，每棵树的训练集都一样，那么最终训练出的树分类结果也是完全一样的
• M维特征，随机抽取k<M个特征进行最优特征的选取：如果每个样本的特征维度为M，指定一个常数m<<M，随机地从M个特征中选取m个特征子集，每次树进行分裂时，从这m个特征中选择最优的

　　每棵树都尽最大程度的生长，并且没有剪枝过程，两个随机性的引入对随机森林的分类性能至关重要。由于它们的引入，使得随机森林不容易陷入过拟合，并且具有很好得抗噪能力（比如：对缺省值不敏感）

 

　　随机森林分类效果（错误率）与两个因素有关：

• 森林中任意两棵树的相关性：相关性越大，错误率越大
• 森林中每棵树的分类能力：每棵树的分类能力越强，整个森林的错误率越低

 

　　减小特征选择个数m，树的相关性和分类能力也会相应的降低；增大m，两者也会随之增大。所以关键问题是如何选择最优的m（或者是范围），这也是随机森林唯一的一个参数

 

四、随机森林工作原理解释的一个简单例子

　描述：根据已有的训练集已经生成了对应的随机森林，随机森林如何利用某一个人的年龄（Age）、性别（Gender）、教育情况（Highest Educational Qualification）、工作领域（Industry）以及住宅地（Residence）共5个字段来预测他的收入层次

　收入层次 :

　　Band 1 : Below $40,000

　　Band 2: $40,000 – 150,000

　　Band 3: More than $150,000

　随机森林中每一棵树都可以看做是一棵CART（分类回归树），这里假设森林中有5棵CART树，总特征个数N=5，我们取m=1（这里假设每个CART树对应一个不同的特征）

　CART 1 : Variable Age

 

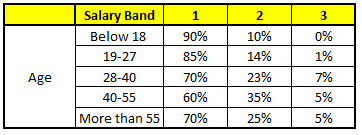
　CART 2 : Variable Gender

　

 

　　

　CART 3 : Variable Education

　

 

 

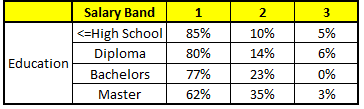
　CART 4 : Variable Residence

　

 

 

　CART 5 : Variable Industry

 

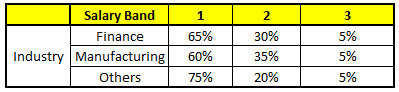
　我们要预测的某个人的信息如下：

　　1. Age : 35 years ; 2. Gender : Male ; 3. Highest Educational Qualification : Diploma holder; 4. Industry : Manufacturing; 5. Residence : Metro

 

　根据这五棵CART树的分类结果，我们可以针对这个人的信息建立收入层次的分布情况：

 

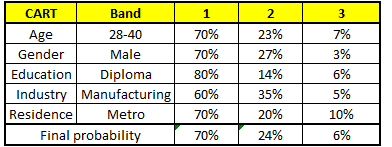
　最后，我们得出结论，这个人的收入层次70%是一等，大约24%为二等，6%为三等，所以最终认定该人属于一等收入层次（小于$40,000）

 

五、简单流程图

　

 

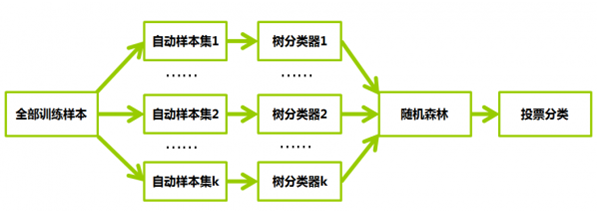
六、随机森林的特征重要性原理

　假设有k棵树组成的RF，那么我们就需要k的自动样本集，如上面的流程图；可是我们只有N个样本组成的一个数据集X，而现在需要k个数据集，这里采用的方法是：

　　从N个样本中通过bootstrap有放回的随机抽取N个新的自主样本，组成第一个自动样本集1（对于该样本集：有可能某个样本被抽中多次），构成树分类器1，而该次未被抽到的样本组成了袋外数据

　　自动样本集2-k也通过bootstrap有放回的随机抽取，构成树分类器2-k，每次抽样的数据集，都会用于树的构建，并且都有各自的袋外数据

 

　小细节：每个袋外数据会对相应的树作预测，评估其误差（称为袋外误差），特征重要性​度量步骤如下，对于某个特征x来说

　1）对每一颗决策树，选择相应的袋外数据（out of bag，OOB）​计算袋外数据误差，记为errOOB1

　　　所谓袋外数据是指，每次建立决策树时，通过重复抽样得到一个数据用于训练​决策树，这时还有大约1/3的数据没有被利用，没有参与决策树的建立。这部分数据可以用于对决策树的性能进行评估，计算模型的预测错误率，称为袋外数据误差

　​2）随机对袋外数据OOB所有样本的特征x加入噪声干扰（可以随机改变样本在特征X处的值），再次计算袋外数据误差，记为errOOB2

　3）​假设森林中有k棵树，则特征x的重要性\(=\sum (errOOB2-errOOB1) / k\)

　　　上面公式之所以能够说明特征的重要性是因为，如果加入随机噪声后，袋外数据准确率大幅度下降（即errOOB2上升），说明这个特征对于样本的预测结果有很大影响，进而说明重要程度比较高

 

七、RF优缺点

　RF的主要优点有：

　　　1） 高度并行化，对于大样本（样本数）训练速度有优势

　　　2） 由于可以随机选择决策树节点划分特征，这样在样本特征维度很高的时候，仍然能高效的训练模型

　　　3） 在训练后，可以给出各个特征对于输出的重要性

　　　4） 由于采用了随机采样，训练出的模型的方差小，泛化能力强

　　　5） 相对于Boosting系列的Adaboost和GBDT， RF实现比较简单

　　　6） 对部分特征缺失不敏感

　　RF的主要缺点有：

　　　1）在某些噪音比较大的样本集上，RF模型容易陷入过拟合

　　　2）取值划分比较多的特征容易对RF的决策产生更大的影响，从而影响拟合的模型的效果  

 

八、RF与GBDT的区别

　1、组成随机森林的树可以是分类树，也可以是回归树；而GBDT只由回归树组成，GBDT的会累加所有树的结果，而这种累加是无法通过分类完成的，因此GBDT的树都是CART回归树，而不是分类树

　2、组成随机森林的树可以并行生成；而GBDT只能是串行生成

　3、对于最终的输出结果而言，随机森林采用多数投票等；而GBDT则是将所有结果累加起来，或者加权累加起来

　4、随机森林对异常值不敏感，GBDT对异常值非常敏感 

　5、随机森林对训练集一视同仁，GBDT是基于权值的弱分类器的集成

　6、随机森林是通过减少模型方差提高性能，GBDT是通过减少模型偏差提高性能