各种检验
1.卡方检验中的k×2表资料:
如考察肿瘤负荷分为高,中,低的患者对药物的反应关系:
| mutations/MB | Response | No Response |
| High(>23.1) | 9 | 2 |
| Intermediate(3.3-23.1) | 4 | 7 |
| Low(<3.3) | 1 | 9 |
x <- c(9,4,1,2,7,9) dim(x) <- c(3,2) chisq.test(x) #返回:X-squared = 11.35, df = 2, p-value = 0.003431
P<0.05,,说明突变负荷与药物反应相关
下面讲解计算过程:
我们先假设突变负荷与药物反应无关,计算出response率 = 14 / (14 + 18) = 0.4375,no response率 = 0.5625
根据上面的独立假设,求出response和no response的理论数:

卡方检验的计算公式为:(下面的T即为上面括号中的数字:理论数)
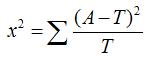
x2用于衡量实际值与理论值的差异程度(也就是卡方检验的核心思想),包含了以下两个信息:
1. 实际值与理论值偏差的绝对大小(由于平方的存在,差异是被放大的)
2. 差异程度与理论值的相对大小
这里$x^2 = (9 - 4.8175) ^ 2 / 4.8175 + (2 - 6.1875) ^ 2 / 6.1875 + (4 - 4.8175) ^ 2 / 4.8175 + (7 - 6.1875) ^ 2 / 6.1875 + (1 - 4.375) ^ 2 / 4.375 + (9 - 5.625) ^ 2 / 5.625 = 11.35$
这里自由度为2,查表得临界卡方值为:5.99,实际卡方值大于临界值,拒绝原假设,也就是突变负荷与药物反应有关系

2.KS检验
使用K-S检验一个数列是否服从正态分布、两个数列是否服从相同的分布
4.Mann-Kendall-Trend趋势分析
git clone https://github.com/mps9506/Mann-Kendall-Trend.git



