维特比算法
一、维特比算法解决的问题
如下图,假如你从S和E之间找一条最短的路径,除了遍历完所有路径(弱爆了),还有什么更好的方法?
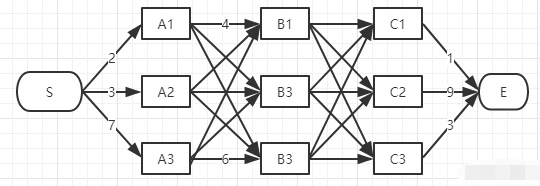
答案:viterbi (维特比)算法。viterbi维特比算法解决的是篱笆型的图的最短路径问题
图的节点按列组织,每列的节点数量可以不一样,每一列的节点只能和相邻列的节点相连,不能跨列相连
节点之间有着不同的距离,距离的值就不在图上一一标注出来了
二、维特比算法过程
为了找出S到E之间的最短路径,我们先从S开始从左到右一列一列地来看
首先起点是S,从S到A列的路径有三种可能:S-A1、S-A2、S-A3,如下图:
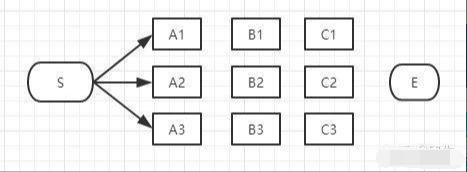
我们不能武断地说S-A1、S-A2、S-A3中的哪一段必定是全局最短路径中的一部分,目前为止任何一段都有可能是全局最短路径的备选项
我们继续往右看,到了B列。按B列的B1、B2、B3逐个分析,先看B1:
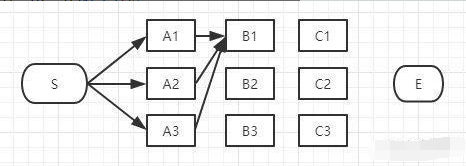
如上图,经过B1的所有路径只有3条:
S-A1-B1
S-A2-B1
S-A3-B1
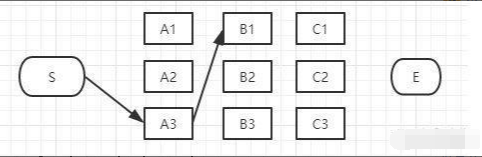
接下来,我们继续看B2:
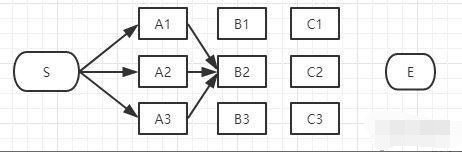
同理,如上图,经过B2的路径有3条:
S-A1-B2
S-A2-B2
S-A3-B2
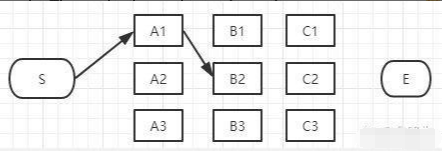
接下来我们继续看B3:
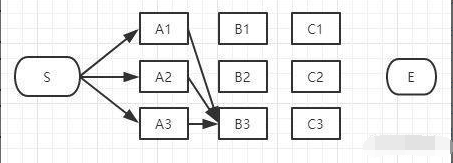
同理,如上图,经过B3的路径也有3条:
S-A1-B3
S-A2-B3
S-A3-B3
这三条路径中我们也肯定可以算出其中哪一条是最短的,假设S-A2-B3是最短的,那么我们就知道了经过B3的所有路径当中S-A2-B3是最短的,其它两条路径路径S-A1-B3和S-A3-B3也可以删掉了。经过B3的所有路径只剩一条,如下图:
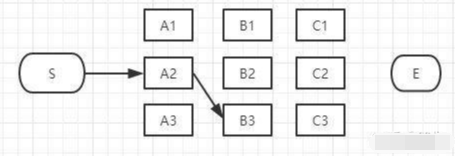
现在对于B列的所有节点我们都过了一遍,B列的每个节点我们都删除了一些不可能是答案的路径,看看我们剩下哪些备选的最短路径,如下图:
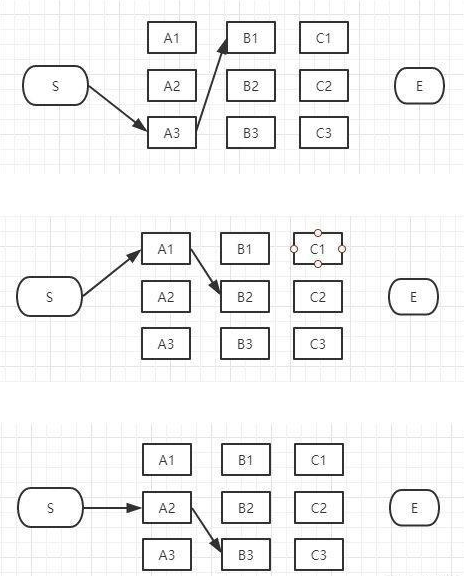
上图是我们删掉了其它不可能是最短路径的情况,留下了三个有可能是最短的路径:S-A3-B1、S-A1-B2、S-A2-B3。
现在我们将这三条备选的路径放在一起汇总到下图:
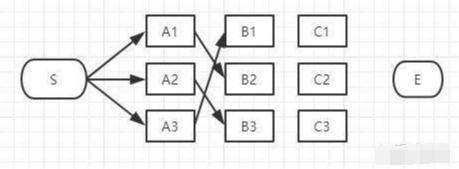
S-A3-B1、S-A1-B2、S-A2-B3都有可能是全局的最短路径的备选路径,我们还没有足够的信息判断哪一条一定是全局最短路径的子路径
如果我们你认为没毛病就继续往下看C列,如果不理解,回头再看一遍,前面的步骤决定你是否能看懂viterbi算法(维特比算法)
接下来讲到C列了,类似上面说的B列,我们从C1、C2、C3一个个节点分析。
经过C1节点的路径有:
S-A3-B1-C1
S-A1-B2-C1
S-A2-B3-C1
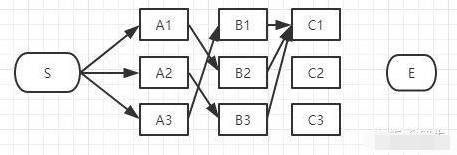
和B列的做法一样,从这三条路径中找到最短的那条(假定是S-A3-B1-C1),其它两条路径同样道理可以删掉了。那么经过C1的所有路径只剩一条,如下图:
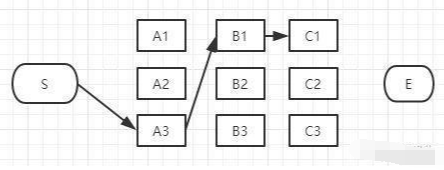
同理,我们可以找到经过C2和C3节点的最短路径,汇总一下:
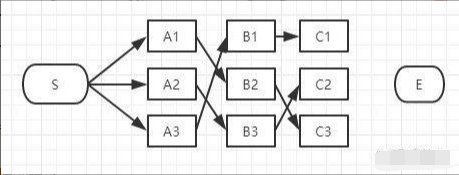
到达C列时最终也只剩3条备选的最短路径,我们仍然没有足够信息断定哪条才是全局最短
最后,我们继续看E节点,才能得出最后的结论
到E的路径也只有3种可能性:
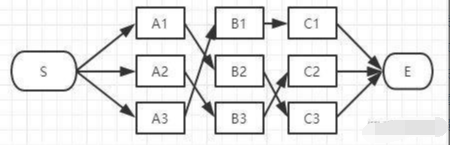
E点已经是终点了,我们稍微对比一下这三条路径的总长度就能知道哪条是最短路径了:
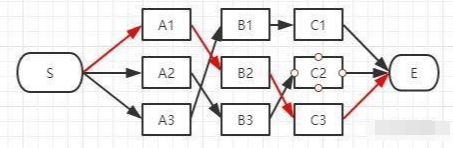
在效率方面相对于粗暴地遍历所有路径,viterbi 维特比算法到达每一列的时候都会删除不符合最短路径要求的路径,大大降低时间复杂度
三、参考




