HMM-隐马尔科夫模型
一、目的
主要以实例讲解HMM,防止公式吓跑大家
HMM两个假设:
- 齐次马尔可夫性假设:当前状态只依赖上一个状态
- 观测独立性假设:当前观测只依赖当前状态
二、实例
假设生活中的天气只有三种状态:sun,cloud,rain,并且我们知道他们之间相互转换的概率,也就是说:
昨天是sun,今天天气转换成sun,cloud,rain的概率我们知道
昨天是cloud,今天天气转换成sun,cloud,rain的概率我们知道
昨天是rain,今天天气转换成sun,cloud,rain的概率我们知道
别问我咋知道,我知道也不告诉你(当然可以根据历史进行统计出来)

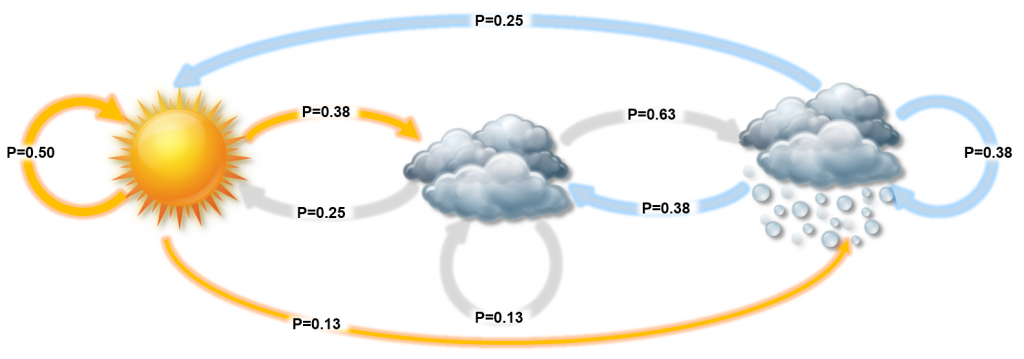
上图进行了四舍五入,其实概率和应该是1
现在还知道一些信息-天气状态对海藻的影响,如天气是sun的情况下,我们观测到的海藻可能是:
海藻为干燥的概率为0.6,微湿的概率为0.2,湿润的概率为0.15,湿透的概率为0.05,这些观测的结果汇总概率为1

我们还知道天气初始状态概率:

好了,隐马尔科夫模型三要素$(A, B, \pi)$,你已经都知道了,可以毕业了(毕业管什么用,照样啥都不会,哈哈),那么到底什么是HMM:
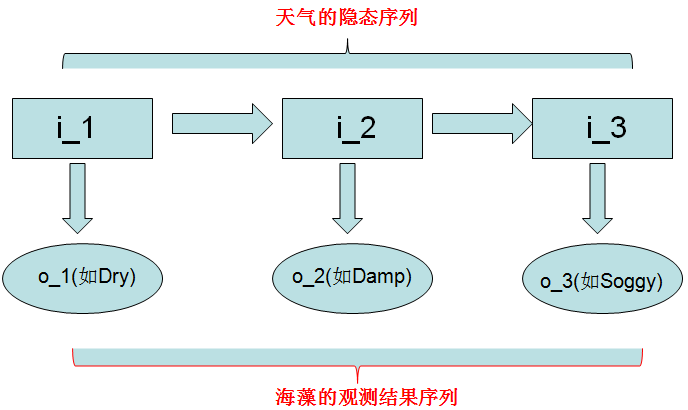
上图的天气状态就是一个隐马尔科夫链:这三天我们不知道天气的隐藏态,但是我们观察到了海藻的干湿程度啦
那么请思考:我们观察到海藻的结果分别为Dry,Damp,Soggy,请问这三天的天气状态最有可能是什么天气状态(其实是HMM预测问题)?
三、HMM的三个基本问题
1)概率计算问题
给定模型$\lambda = (A, B, \pi)$和观察序列$O=(o_1, o_2, o_3, ..., o_T)$,计算在模型$\lambda $下观察序列$O$出现的概率:$P(O|\lambda)$
如上面的图片:我们想知道在模型$\lambda = (A, B, \pi)$下$O=(Dry, Damp, Soggy)$出现的概率$P(O|\lambda)$
先介绍概念上可行但是计算上不可行的直接计算法:因为每种隐藏状态序列(天气状态)都能产生$O=(Dry, Damp, Soggy)$的观测结果,我们需要列举出所有可能的状态序列,然后求出每种状态序列产生$O=(Dry, Damp, Soggy)$的概率,然后进行加和,看下面
我们先假设隐藏的天气状态是:sun,sun,sun(这里隐藏的天气状态排列组合数目是:3 * 3 * 3 = 27)
由于初始天气状态概率分布为:$\pi = {1, 0, 0}$
所以第一天(t = 1)的天气状态就变成了:$\pi * A = [0.5, 0.375, 0.125]$,也就是下面:
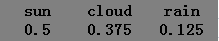
所以第一天出现海藻Dry的概率是:$P = 0.5 * P(Dry|sun) = 0.5 * 0.6 = 0.3$(我们已经假设第一天的天气为sun-可能性是0.5)
第二天(t = 2)的天气状态依赖于第一天的天气状态($[0.5, 0.375, 0.125]$:我们可以将其赋值给$\pi$,即$\pi = [0.5, 0.375, 0.125]$)
所以第二天的天气状态是:$\pi * A = [0.375, 0.281, 0.344]$
第二天出现海藻Damp的概率是:$P = 0.375 * P(Damp|sun) = 0.375 * 0.15 = 0.056$
同理,第三天(t=3)的天气状态依赖于第二天的天气状态:($[0.375, 0.281, 0.344]$,我们可以将其赋值给$\pi$,即$\pi = [0.375, 0.281, 0.344]$)
所以第三天的天气状态是:$\pi * A = [0.344, 0.305, 0.352]$
第三天出现海藻Soggy的概率是:$P = 0.344 * P(Soggy|sun) = 0.344 * 0.05 = 0.017$
所以我们列举的第一个状态序列:sun, sun, sun产生海藻Dry,Damp,Soggy结果的概率就是:
$P(Dry, Damp, Soggy | sun,sun,sun) = 0.3 * 0.056 * 0.017 = 0.0002856$
小规律:就是我们每一天的天气状态可以用$\pi * A^t$,我们的$t$就是第$t$天
这种列举的方法是不可取的,因为我们的天气状态集合目前只有三个,序列也只有三天,如果我们序列再长些,天气状态再多些,你都无法一一列举每种隐藏状态序列:(目前是$3^3=27$,还好一一列举)
解决方案是:前向与后向算法
前向算法:
1)计算时刻1的各个隐藏状态前向概率:$\alpha_{1}(i)=\pi_{i} b_{i}\left(o_{1}\right), i=1,2, \ldots N$(假设有N个隐藏态,这里N为3,即3个天气状态)
2)递推时刻$2,3,4,...,T$时刻的前向概率:$\alpha_{t+1}(i)=\left[\sum_{j=1}^{N} \alpha_{t}(j) a_{j i}\right] b_{i}\left(o_{t+1}\right), i=1,2, \ldots N$
3)计算最终结果:$P(O \mid \lambda)=\sum_{i=1}^{N} \alpha_{T}(i)$即第T个时刻各个状态前向概率之和
前向算法实例-
1)时刻1是Dry:
隐藏状态是Sun的概率为:$\alpha_{1}(Sun)=\pi_{Sun} b_{Sun}\left(o_{1}\right)=1.0 \times 0.6=0.6$
隐藏状态是Cloud的概率为:$\alpha_{1}(Cloud)=\pi_{Cloud} b_{Cloud}\left(o_{1}\right)=0 \times 0.25=0$
隐藏状态是Rain的概率为:$\alpha_{1}(Rain)=\pi_{Rain} b_{Rain}\left(o_{1}\right)=0 \times 0.05=0$
2)现在我们可以开始递推了,首先递推时刻2,时刻3三个状态的前向概率:
时刻2是Damp,隐藏状态是Sun的概率为:$\alpha_{2}(Sun)=[0.6 * 0.5+0 * 0.25+0 * 0.25] \times 0.15=0.045$(解释:即第一个前向概率转移到下一个的概率,Sun可以转向Sun,Cloud可以转向Sun,Rain也可以转向Sun,三者转向之和后再乘以Sun条件下Damp概率)
时刻2是Damp,隐藏状态是Cloud的概率为:$\alpha_{2}(Cloud)=[0.6 * 0.375 + 0 * 0.125 + 0 * 0.375] \times 0.25=0.056$(解释:即第一个前向概率转移到下一个的概率,Sun可以转向Cloud,Cloud可以转向Cloud,Rain也可以转向Cloud,三者转向之和后再乘以Cloud条件下Damp概率)
时刻2是Damp,隐藏状态是Rain的概率为:$\alpha_{2}(Rain)=[0.6 * 0.125 + 0 * 0.625 + 0 * 0.375] \times 0.35=0.026$(解释:即第一个前向概率转移到下一个的概率,Sun可以转向Rain,Cloud可以转向Rain,Rain也可以转向Rain,三者转向之和后再乘以Rain条件下Damp概率)
时刻3是Soggy,隐藏状态是Sun的概率为:$\alpha_{3}(Sun)=[0.045 * 0.5+0.056 * 0.25+0.026 * 0.25] \times 0.05=0.002$(解释:即第一个前向概率转移到下一个的概率,Sun可以转向Sun,Cloud可以转向Sun,Rain也可以转向Sun,三者转向之和后再乘以Sun条件下Soggy概率)
时刻3是Soggy,隐藏状态是Cloud的概率为:$\alpha_{3}(Cloud)=[0.045 * 0.375+0.056 * 0.125+0.026 * 0.375] \times 0.25=0.008$(解释:即第一个前向概率转移到下一个的概率,Sun可以转向Sun,Cloud可以转向Sun,Rain也可以转向Sun,三者转向之和后再乘以Cloud条件下Soggy概率)
时刻3是Soggy,隐藏状态是Rain的概率为:$\alpha_{3}(Rain)=[0.045 * 0.125+0.056 * 0.625+0.026 * 0.375] \times 0.5=0.025$(解释:即第一个前向概率转移到下一个的概率,Sun可以转向Sun,Cloud可以转向Sun,Rain也可以转向Sun,三者转向之和后再乘以Rain条件下Soggy概率)
3)计算最终结果:
观测状态序列:{Dry,Damp,Soggy}的概率为:$0.002 + 0.008 + 0.025 = 0.035$
从递推公式可以看出,我们的算法时间复杂度是$O(TN^2)$,比暴力解法的时间复杂度$O(TN^T)$少了几个数量级
后向算法:
参考1-https://zhuanlan.zhihu.com/p/41912745(有些计算上的错误)

参考2-https://blog.csdn.net/zb1165048017/article/details/48577891
- 第三个观测值Soggy来自Sun:$\beta_{Soggy}(Sun) = 1$(初始化)
- 第三个观测值Soggy来自Cloud:$\beta_{Soggy}(Cloud) = 1$(初始化)
- 第三个观测值Soggy来自Rain:$\beta_{Soggy}(Rain) = 1$(初始化)
- 第二个观测值Damp来自Sun:(Sun可以转向下一个状态Sun,Cloud或者Rain对应的Soggy):$\beta_{Damp}(Sun) = 0.5*0.05*1 + 0.375*0.25*1 + 0.125*0.5*1 = 0.18125$
- 第二个观测值Damp来自Cloud:(Cloud可以转向下一个状态Sun,Cloud或者Rain对应的Soggy):$\beta_{Damp}(Cloud) = 0.25*0.05*1 + 0.125*0.25*1 + 0.625*0.5*1 = 0.35625$
- 第二个观测值Damp来自Rain:(Rain可以转向下一个状态Sun,Cloud或者Rain对应的Soggy):$\beta_{Damp}(Rain) = 0.25*0.05*1 + 0.375*0.25*1 + 0.375*0.5*1 = 0.29375$
- 第一个观测值Dry来自Sun:(Sun可以转向下一个状态Sun,Cloud或者Rain对应的Damp):$\beta_{Dry}(Sun) = 0.5*0.15*0.18125 + 0.375*0.25*0.35625 + 0.125*0.35*0.29375 = 0.05984375$
- 第一个观测值Dry来自Cloud:(Cloud可以转向下一个状态Sun,Cloud或者Rain对应的Damp):$\beta_{Dry}(Cloud) = 0.25*0.15*0.18125+ 0.125*0.25*0.35625 + 0.625*0.35*0.29375 = 0.0821875$
- 第一个观测值Dry来自Rain:(Rain可以转向下一个状态Sun,Cloud或者Rain对应的Damp):$\beta_{Dry}(Rain) = 0.25*0.15*0.18125 + 0.375*0.25*0.35625 + 0.375*0.35*0.29375 = 0.07875$
- 逆向思考第一个观测是怎么来的?如何得知是从哪个隐态得到的?答曰:初始值,所以结合初始值,这一条完整的“路径”才算走完
- 第一个观测值Dry来自Sun(结合初始值):$\beta'_{Dry}(Sun) = 1 * 0.6 * \beta_{Dry}(Sun) = 0.6 * 0.05984375 = 0.036$
- 第一个观测值Dry来自Cloud(结合初始值):$\beta'_{Dry}(Cloud) = 0 * 0.25 * \beta_{Dry}(Cloud) = 0 * 0.0821875 = 0$
- 第一个观测值Dry来自Rain(结合初始值):$\beta'_{Dry}(Rain) = 0 * 0.05 * \beta_{Dry}(Rain) = 0 * 0.07875 = 0$
- 观测状态序列:{Dry,Damp,Soggy}的概率为:$0.036 + 0 + 0 = 0.036$和前向计算结果一致
2)学习问题
即参数估计问题:假设HMM的观测序列是“干燥,潮湿,湿透,…”,那么,HMM的参数$A,B,pi$如何设置,才能使这个观测序列出现的概率最大?
这就是所谓的隐马尔可夫模型参数估计问题。
HMM的参数学习问题有两种:
1)监督学习:给定观测序列$O={\left(o_{1}, \ldots, o_{T}\right)}$和对应的状态序列$I={\left(i_{1}, \ldots, i_{T}\right)}$,估计参数$\lambda = (A, B, \pi)$
训练数据已经标明了观测序列和对应的状态序列,则状态转换概率为:$P(t \mid s)=\frac{\operatorname{Count}(t, s)}{\operatorname{Count}(s)}$,发射概率为:$P(w \mid t)=\frac{\operatorname{Count}(w, t)}{\operatorname{Count}(t)}$,$\pi$可以根据状态序列求期望即可获得
2)非监督学习:只给定观测序列$O={\left(o_{1}, \ldots, o_{T}\right)}$,估计参数$\lambda = (A, B, \pi)$
很多时候我们没有标注数据,只有很多组观测序列,我们无法像上面那样就行参数估计,但我们可以比较两组不同的参数,判断谁得到样本集的概率更高,EM算法能帮助我们在这种情况下获得概率分布参数的局部最优解。Baum-Welch算法就是EM算法在HMM上的具体实现
3)预测问题-也叫解码(decoding)问题
就是给定了观测序列(如上面的Dry, Damp, Soggy),求最有可能的对应的状态序列(如上面:求最有可能的天气状态序列-你可以像概率计算问题中的直接计算方法一样,求出每种状态序列的概率,然后挑出来最大的概率对应的状态序列,但是计算是海量的,无法操作的)
求最大可能的状态序列的方法就是-动态规划之维特比算法
HMM应用维特比算法不同的地方在于状态转移都是概率了,最可能的状态序列是概率相乘最大,而不是我们看到的路径相加最短
1)初始化

其实这里我们还看不出来走哪条路径概率最大,因为他们要和后面的概率相乘才能看出哪条最优
接下来我们让第一天的三种天气状态转移到sun状态,我们找出其中的最大概率

可见最大概率是sun ---> sun,我们删掉其他两条路径

接下来我们让第一天的三种天气状态转移到cloud状态,我们找出其中的最大概率

可见最大概率是sun ---> cloud,我们删掉其他两条路径
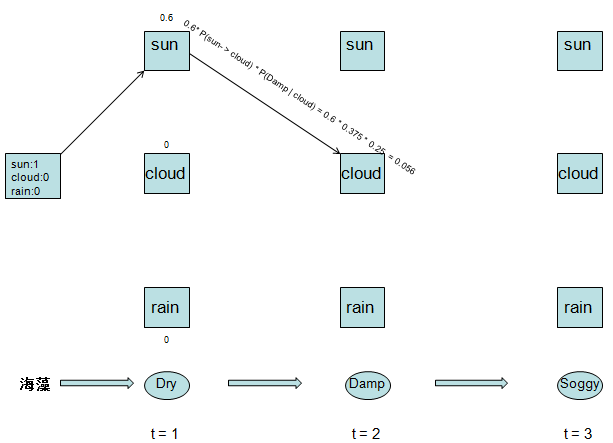
接下来我们让第一天的三种天气状态转移到rain状态,我们找出其中的最大概率
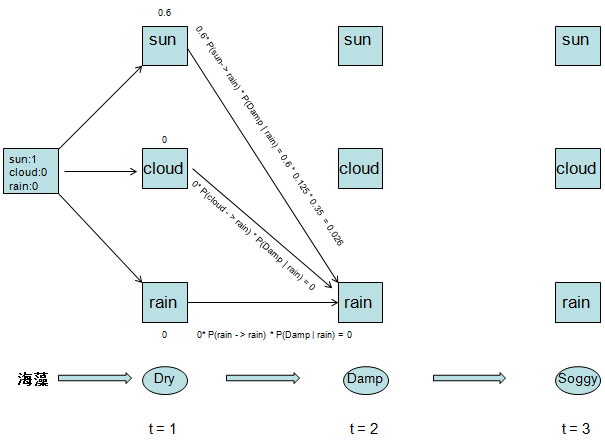
可见最大概率是sun ---> rain,我们删掉其他两条路径
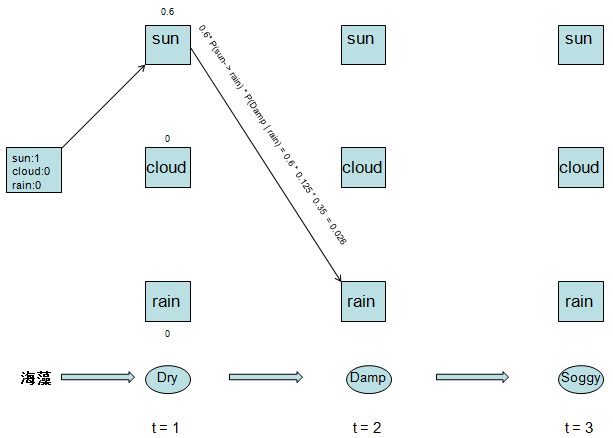
然后我们将第二天的三种最优结果进行合并:

到这里我们还不能确定哪条路径概率最大(虽然sun --> cloud的概率是0.056,目前最大,但是不一定说最优路径一定经过该路径),我们继续
接下来我们让第二天的三种天气状态转移到第三天的sun状态,我们找出其中的最大概率
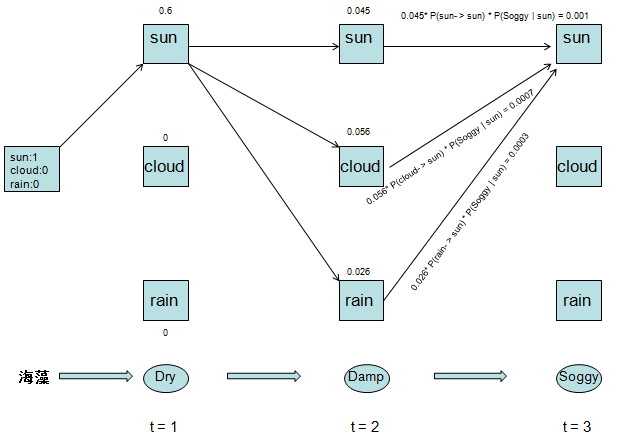
可见,sun --> sun概率最大,我们删掉其他路径

接下来我们让第二天的三种天气状态转移到第三天的cloud状态,我们找出其中的最大概率
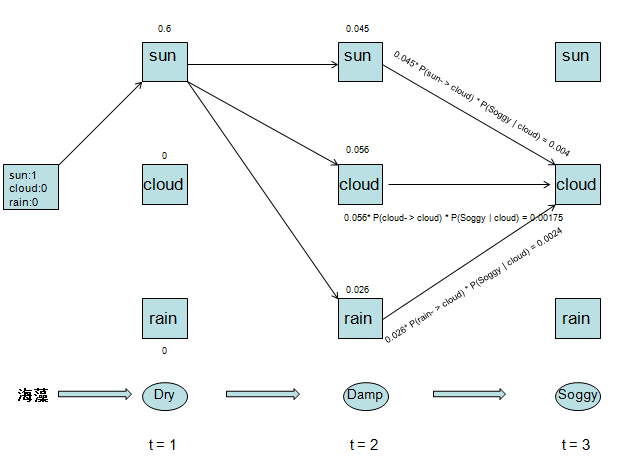
可见,sun --> cloud概率最大,我们删掉其他路径
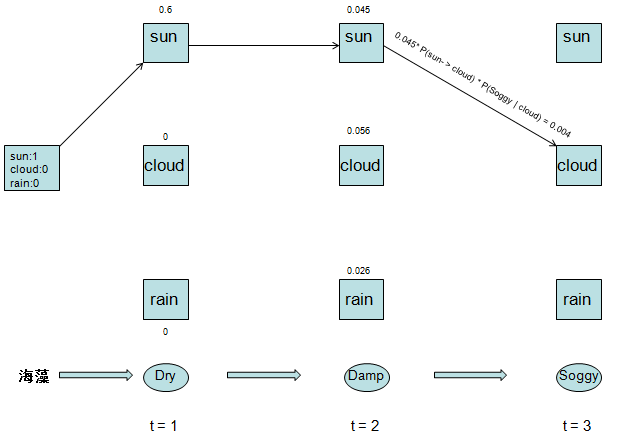
接下来我们让第二天的三种天气状态转移到第三天的rain状态,我们找出其中的最大概率
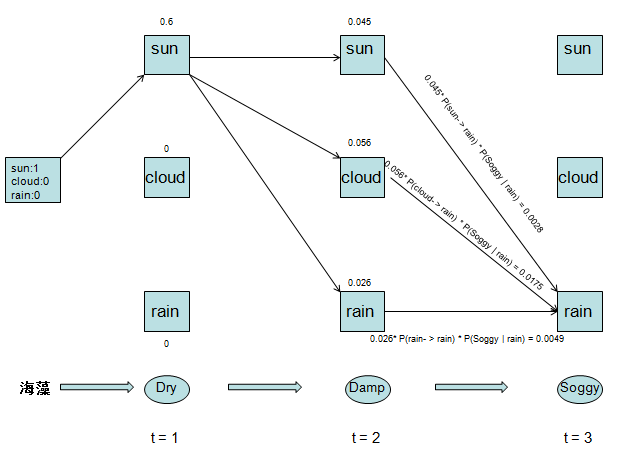
可见,cloud --> rain概率最大,我们删掉其他路径
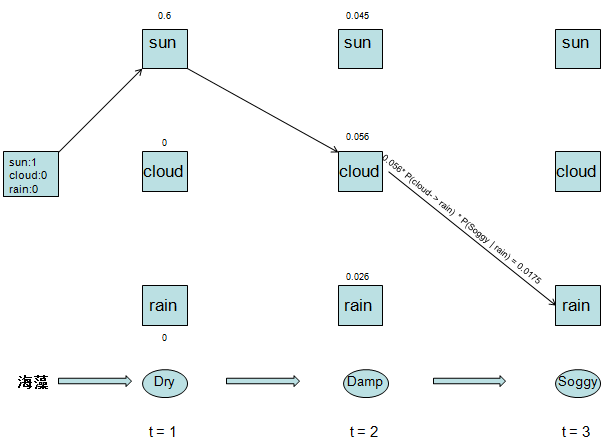
然后我们将第三天的三种最优结果进行合并:

通过回溯,我们找到全局最优路径,也就是最佳的天气状态序列:
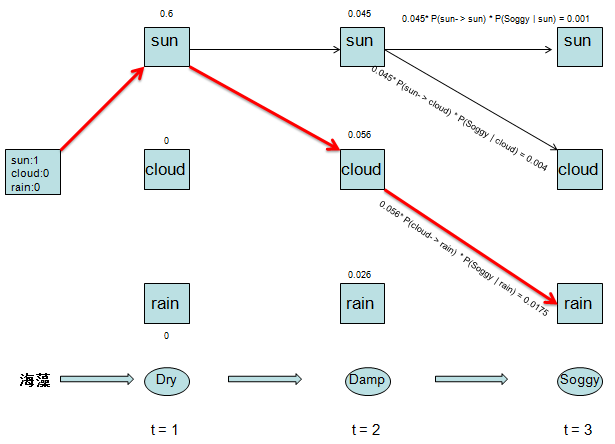
最优天气状态序列是:sun --> cloud --> rain
这个结果比直接计算每种天气状态序列的概率,然后比较概率大小,取最大概率对应的天气状态序列一致,但是速度更快
三、参考
https://www.cnblogs.com/sss-justdDoIt/p/10218852.html
https://zhuanlan.zhihu.com/p/87573049


