08-求解Ax=b：可解性和解的结构

一、增广矩阵

　假设我们要求解方程$Ax=b$，其中矩阵$A$和$b$如下所示：

$A = \left[\begin{array}{llll}{1} & {2} & {2} & {2} \\ {2} & {4} & {6} & {8} \\ {3} & {6} & {8} & {10}\end{array}\right]$

$b = \left[\begin{array}{llll}{b_1}\\ {b_2}\\{b_3}\end{array}\right]$

　我们可以在矩阵$A$右侧加上一列b，得到：

$\left[\begin{array}{llll}{1} & {2} & {2} & {2} & {b_1} \\ {2} & {4} & {6} & {8}& {b_2} \\ {3} & {6} & {8} & {10}& {b_3}\end{array}\right]$

此即为增广矩阵：即A和b一块二考虑

 

二、可解性

　方程$Ax=b$可解的条件是：当$b$属于$A$的列空间（ C(A) ）时，也就是$b$是$A$的列向量的线性组合

　换一种说法：如果矩阵$A$各行的线性组合得到零，那么$b$分量执行相同的操作也必须得到零向量（参考上面的矩阵$A$）

　只有$b$满足了上面的条件，方程才有解

 

三、求$Ax=b$所有解

　第一步：求一个特解

　　将所有自由变量设为0

　　我们将增广矩阵进行消元后：

$\begin{array}{l}{\left[\begin{array}{}{1} & {2} & {2} & {2} & {b_{1}} \\ {0} & {0} & {2} & {4} & {b_{2}-2 b_{1}} \\ {0} & {0} & {0} & {0} &{b_{3}-b_{2}-b_{1}}\end{array}\right]} \\ {} \end{array}$

　　方程有解的条件便是：$O=b_{3}-b_{2}-b_{1}$，假设$b=\left[\begin{array}{l}{1} \\ {5} \\ {6}\end{array}\right]$，则消元矩阵为：

$\begin{array}{l}{\left[\begin{array}{}{1} & {2} & {2} & {2} & {1} \\ {0} & {0} & {2} & {4} & {3} \\ {0} & {0} & {0} & {0} &{0}\end{array}\right]} \\ {}\end{array}$

　　然后求出主变量：

　　　针对上面的例子，$x_2, x_4 = 0$，则求主变量过程简化为：

$x_{1}+2 x_{3}=1$
$2 x_{3}=3$

　　　于是一个特解为：$x_p = \left[\begin{array}{c}{-2} \\ {0} \\ {3/2} \\ {0}\end{array}\right]$

 

　　还记得07）节中的零空间吗？可以去看看，于是我们的通解为：即特解和零空间（在假设的$b$的情况下）

$X = \left[\begin{array}{c}{-2} \\ {0} \\ {3/2} \\ {0}\end{array}\right]+C_{1}\left[\begin{array}{c}{-2} \\ {1}\\ {0} \\ {0}\end{array}\right]+ C_{2}\left[\begin{array}{c}{2} \\ {0} \\ {-2} \\ {1}\end{array}\right]$

注意：这里的特解是与$b$的值相关的

 

　　那么为什么这样的组合可以组成方程的通解呢？原因如下：

$Ax_p = b$

$Ax_n = 0$

两者相加：$A(x_p + x_n) = b$

其中$x_p$是$b$给定下的特解，$x_n$是零空间，所以通解就是特解加零空间

 

　　也就是：

 

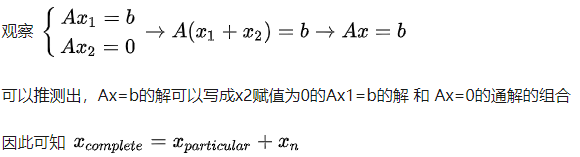
四、秩（Rank）

　矩阵的秩等于矩阵的主元数。如果矩阵的秩为r，则必有r<=m且r<=n，下面讨论满秩（full rank）的情形：

　列满秩：r=n。每列都有主元，x的每一个分量都是主变量，没有自由变量。零空间N(A)之内只有零向量。方程无解或者有唯一解，如下

　　为何列满秩时，零空间N(A)之内只有零向量？因为之前我们讲过零空间定义，该实例中满足$Ax=0$的$x$只有零向量，该实例中的列向量的线性组合无法得到零向量，所以列满秩时，零空间N(A)之内只有零向量。而该实例方程的通解就只剩下特解了，而特解取决于$b$，只有$b$正好是$A$列的线性组合时，方程才有唯一解

$A=\left[\begin{array}{ll}{1} & {3} \\ {2} & {1} \\ {6} & {1} \\ {5} & {1}\end{array}\right] \rightarrow\left[\begin{array}{ll}{1} & {0} \\ {0} & {1} \\ {0} & {0} \\ {0} & {0}\end{array}\right]=R$

 

　行满秩：r=m。每行都有主元，无论b取何值，方程Ax=b都有解。主变量r个，自由变量n-r个，如下

$A=\left[\begin{array}{llll}{1} & {2} & {6} & {5} \\ {3} & {1} & {1} & {1}\end{array}\right] \rightarrow\left[\begin{array}{llll}{1} & {0} & {*} & {*} \\ {0} & {1} & {*} & {*}\end{array}\right]=R$

 

　满秩r=m=n，矩阵可逆。零空间只有零向量，无论b取何值，方程$Ax=b$都有唯一解

$A=\left[\begin{array}{ll}{1} & {2} \\ {3} & {1}\end{array}\right] \rightarrow\left[\begin{array}{ll}{1} & {0} \\ {0} & {1}\end{array}\right]=R$

 

　综上：秩决定了方程组解的数量