02-矩阵消元
本博客是学习MIT-线性代数笔记，Gilbert Strang大神讲的通俗易懂，感兴趣的可以观看视频
其中习题集请点击
一、消元
现在我们有一个方程组，如何求解呢？消元法是个不错的方法：
$\begin{array}{c}{x+2 y+z=2} \\ {3 x+8 y+z=12} \\ {4 y+z=2}\end{array}$
我们用矩阵形式来表示上面的方程组：
$A=\left|\begin{array}{lll}{1} & {2} & {1} \\ {3} & {8} & {1} \\ {0} & {4} & {1}\end{array}\right|$
$b=\left|\begin{array}{c}{2} \\ {12} \\ {2}\end{array}\right|$
$x=\left|\begin{array}{l}{x} \\ {y} \\ {z}\end{array}\right|$
要求解方程组，也就是我们需要获取一个向量$x$，使得：
$Ax=b$
如何进行消元呢？ 消元的目的就是把矩阵$A$变成上三角矩阵$U$：
$A=\left|\begin{array}{lll}{1} & {2} & {1} \\ {3} & {8} & {1} \\ {0} & {4} & {1}\end{array}\right|$ ===》（第二行减去第一行乘以3）$\left|\begin{array}{lll}{1} & {2} & {1} \\ {0} & {2} & {-2} \\ {0} & {4} & {1}\end{array}\right|$ ===》（第三行减去第二行乘以2）$U=\left|\begin{array}{ccc}{1} & {2} & {1} \\ {0} & {2} & {-2} \\ {0} & {0} & {5}\end{array}\right|$
注意：这里的1，2，5是主元，消元的过程中主元不能是0
对向量$b$执行相同的操作：
$b=\left|\begin{array}{c}{2} \\ {12} \\ {2}\end{array}\right|$ ===》（第二行减去第一行乘以3）$\left|\begin{array}{c}{2} \\ {6} \\ {2}\end{array}\right|$ ===》（第三行减去第二行乘以2）$c=\left|\begin{array}{c}{2} \\ {6} \\ {-10}\end{array}\right|$
经过消元，其实我们获得下面的方程组：
$\begin{aligned} x+2 y+z &=2 \\ 2 y-2 z &=6 \\ 5 z &=-10 \end{aligned}$
然后回代：
$5z=-10$，所以$z=-2$，从而求得$x=\left|\begin{array}{c}{2} \\ {1} \\ {-2}\end{array}\right|$
二、行向量与矩阵相乘
前面我们讲了矩阵和列向量相乘，几何意义就是矩阵列向量的线性组合，如果我们反过来呢？
我们想想一个行向量和矩阵相乘的意义又是什么呢？可以理解成矩阵的行向量的线性组合
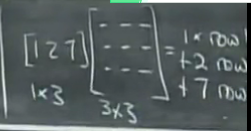
三、矩阵消元可以借助一个矩阵来实现
前面已经讲解了矩阵和列向量相乘的几何解释（矩阵列向量的线性组合），又反过来讲了行向量和矩阵相乘的几何解释（矩阵行向量的线性组合）
有了前面两步讲解，我们知道消元的过程，每一步消元的结果可以通过矩阵来实现，比如：上面第一步讲解中第二行减去第一行乘以3
$A=\left|\begin{array}{lll}{1} & {2} & {1} \\ {3} & {8} & {1} \\ {0} & {4} & {1}\end{array}\right|$ ===》（第二行减去第一行乘以3）$\left|\begin{array}{lll}{1} & {2} & {1} \\ {0} & {2} & {-2} \\ {0} & {4} & {1}\end{array}\right|$
这一步如何借助一个矩阵来实现呢？
通过消元过程我们发现该步骤是矩阵的行进行了线性组合，原来单位矩阵$E=\left|\begin{array}{lll}{1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {0} & {1}\end{array}\right|$，单位矩阵与任何矩阵相乘还是矩阵本身，对该单位矩阵进行行的线性组合：第二行减去第一行乘以3，即
$E_{21}=\left|\begin{array}{lll}{1} & {0} & {0} \\ {-3} & {1} & {0} \\ {0} & {0} & {1}\end{array}\right|$
也就是这个矩阵与原矩阵相乘得到消元后的矩阵
$\left|\begin{array}{lll}{1} & {2} & {1} \\ {0} & {2} & {-2} \\ {0} & {4} & {1}\end{array}\right|$
而第二步是第三行减去第二行乘以2，我们需要什么样的矩阵来实现这个过程呢？同理，应该从单位矩阵转化而来：
$E_{32}=\left|\begin{array}{lll}{1} & {0} & {0} \\ {0} & {1} & {0} \\ {0} & {-2} & {1}\end{array}\right|$
注意：上面的E代表单位矩阵，E数字下标代表初等矩阵（单位矩阵一步转化而来）
综上：消元的每一个我们都可以用一个初等矩阵来实现，我们把每一个合并，即$E_{32}(E_{21}A) = U$，$U$表示消元后矩阵（你看看有多么的简洁明了）
思考一下：如果现在我想从$A$矩阵一步到位得到消元矩阵$U$，可以借助哪个矩阵来实现呢？矩阵结合率告诉我们这个帮忙的矩阵会是：$(E_{32}E_{21})$，即$(E_{32}E_{21})A=U$
四、如何检验结果矩阵中的某一元素的来源？
比如：现在要检验结果矩阵中第二行第三列元素的来源
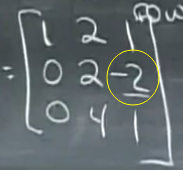
这个-2来自第一个矩阵的第二行和第二个矩阵的第三列的点乘
