弗洛伊德算法
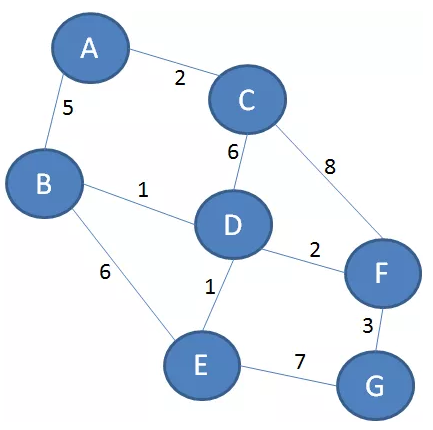
1.要实现Floyd算法,首先需要构建带权图的邻接矩阵:

在邻接矩阵当中,每一个数字代表着从某个顶点到另一个顶点的直接距离,这个距离是没有涉及到任何中继顶点的
2.此时假定只允许以顶点A作为中继顶点,那么各顶点之间的距离会变成什么样子呢?
B和C之间的距离原本是无穷大,此时以A为中继,距离缩短为AB距离+AC距离=5+2=7。更新对应矩阵元素(橙色区域代表顶点A到其他顶点的临时距离):

3.接下来以顶点A、B作为中继顶点,那么各顶点之间的距离会变成什么样子呢?
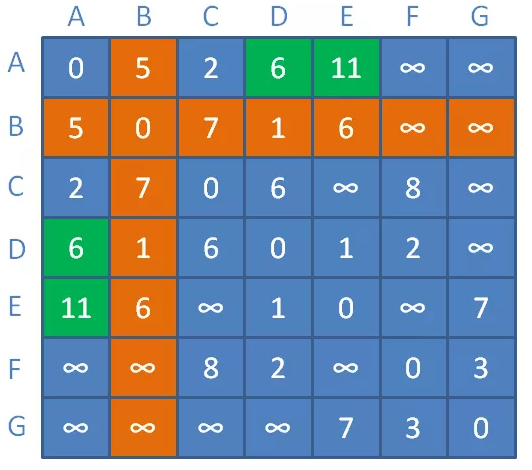
A和D之间的距离原本是无穷大,此时以B为中继,距离缩短为AB距离+BD距离=5+1=6。
A和E之间的距离原本是无穷大,此时以B为中继,距离缩短为AB距离+BE距离=5+6=11。
更新对应矩阵元素(橙色区域代表顶点B到其他顶点的临时距离):
4.接下来以顶点A、B、C作为中继顶点,那么各顶点之间的距离会变成什么样子呢?
A和F之间的距离原本是无穷大,此时以C为中继,距离缩短为AC距离+CF距离=2+8=10。
更新对应矩阵元素(橙色区域代表顶点C到其他顶点的临时距离):

以此类推,我们不断引入新的中继顶点,不断刷新矩阵中的临时距离。最终,当所有顶点都可以作为中继顶点时,我们的距离矩阵更新如下:
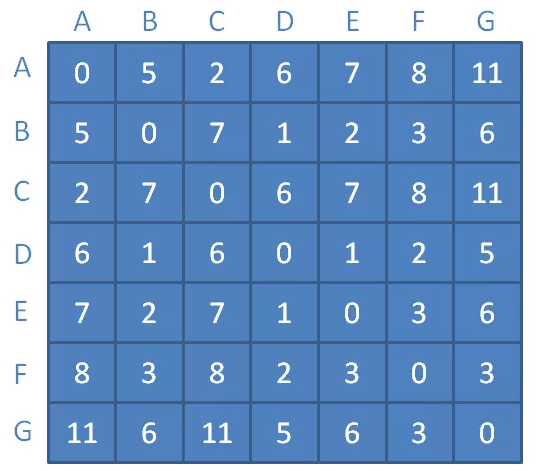
此时,矩阵中每一个元素,都对应着某顶点到另一个顶点的最短距离





