霍夫曼树

一、什么是霍夫曼树

　给定n个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为霍夫曼树(Huffman Tree)

　如下所示两棵二叉树：

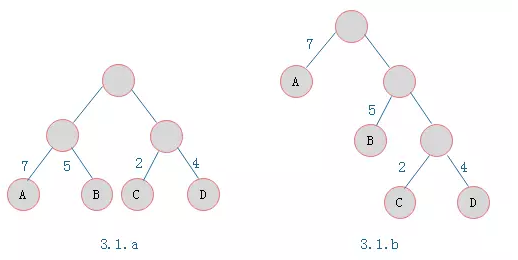
　　叶子结点为A、B、C、D，对应权值分别为7、5、2、4

　　3.1.a树的WPL = 7 * 2 + 5 * 2 + 2 * 2 + 4 * 2 = 36

　　3.1.b树的WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3 = 35

　　由ABCD构成叶子结点的二叉树形态有许多种，但是WPL最小的树只有3.1.b所示的形态。则3.1.b树为一棵霍夫曼树

 

二、霍夫曼树构建过程

　输入：权值为(w1,w2,...wn)的n个节点

　输出：对应的霍夫曼树

　过程：

 

　　1）将(w1,w2,...wn)看做是有n棵树的森林，每个树仅有一个节点

　　2）在森林中选择根节点权值最小的两棵树进行合并，得到一个新的树，这两颗树分布作为新树的左右子树。新树的根节点权重为左右子树的根节点权重之和

　　3） 将之前的根节点权值最小的两棵树从森林删除，并把新树加入森林

　　4）重复步骤2）和3）直到森林里只有一棵树为止

 

　下面我们用一个具体的例子来说明霍夫曼树建立的过程，我们有(a,b,c,d,e,f)共6个节点，节点的权值分布是(16,4,8,6,20,3)

　首先是最小的b和f合并，得到的新树根节点权重是7，此时森林里5棵树，根节点权重分别是16,8,6,20,7。此时根节点权重最小的6,7合并，得到新子树，依次类推，最终得到下面的霍夫曼树

　　

　

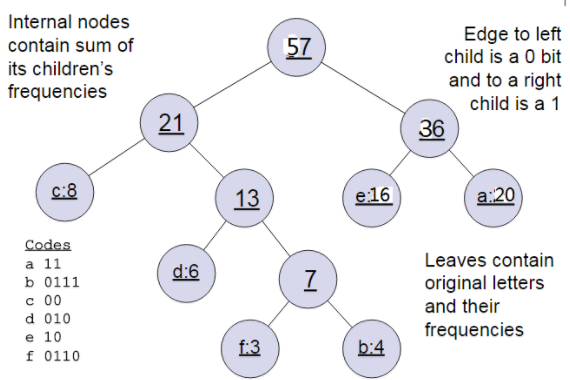
　一般得到霍夫曼树后我们会对叶子节点进行霍夫曼编码，由于权重高的叶子节点越靠近根节点，而权重低的叶子节点会远离根节点，这样我们的高权重节点编码值较短，而低权重值编码值较长

　这保证的树的带权路径最短，也符合我们的信息论，即我们希望越常用的词拥有更短的编码。如何编码呢？一般对于一个霍夫曼树的节点（根节点除外），可以约定左子树编码为0，右子树编码为1.如上图，则可以得到c的编码是00

　在word2vec中，约定编码方式和上面的例子相反，即约定左子树编码为1，右子树编码为0，同时约定左子树的权重不小于右子树的权重