【机器学习经典算法源码分析系列】-- 逻辑回归

1.逻辑回归（Logistic Regression）又常被成为“逻辑斯蒂回归”，实质上是一个二元分类问题。

逻辑回归代价函数：

 

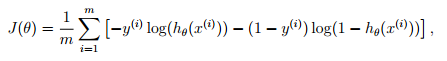
代价函数导数：

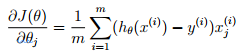
Matlab实现：

 

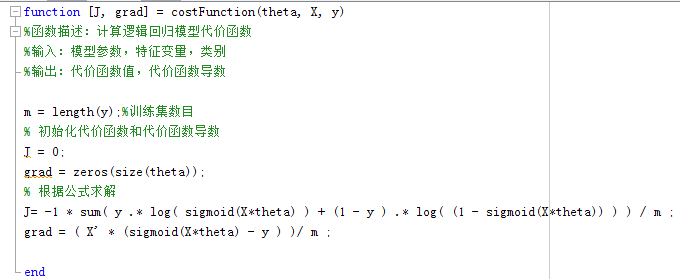
采用matlab中自带的无约束最小化函数fminunc来代替梯度下降法（避免学习率的选择）。

fminunc高级函数的使用参考：http://blog.csdn.net/gzp444280620/article/details/49272977

  

自定义函数与fminunc函数之间的调用关系：

 

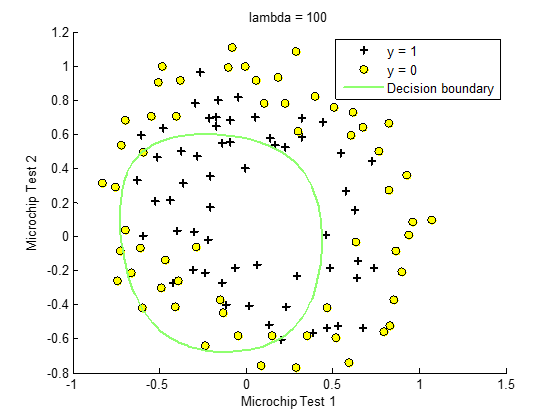
对于二维线性或者非线性问题，我们可以通过画出决策边界来可视化数据集，从而更直观判断模型的准确度。

 

对于可以用简单线性划分的数据集，不需要进行模型复杂度和正则化处理，应用起来往往很简单。

 

2.非线性决策边界问题：

对于边界复杂问题，简单的线性边界划分无法实现，需要增加特征变量的阶数来实现非线性划分。这样就会导致模型的复杂度增加，如何权衡模型的准确度和复杂度？——正则化处理。

 

1）非线性模型复杂度的选择：下面的代码只针对二维特征变量，单一特征变量的最高阶数可以自行试凑。

 

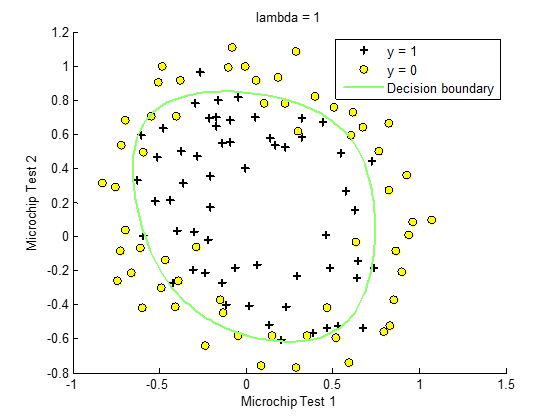
2）正则化参数的选择：

过小：对模型复杂度惩罚不够，过拟合

过大：模型太过简单，训练准确率下降，欠拟合

 

 

正则化处理后的代价函数：

 

代价函数导数：

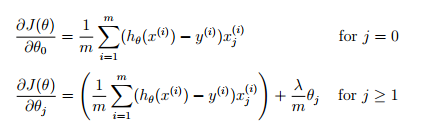
正则化代码：

 

 

PS: 应用逻辑回归模型也可以进行多类分类，处理方法是多次重复进行二分类，每次选择一个正向类，其余各类都视作负向类。

 

个人笔记：http://www.cnblogs.com/always-chang/p/5935655.html

源码分析：http://pan.baidu.com/s/1nu7rwVZ 密码：2ra2