As a reader --> Model-Targeted Poisoning Attacks: Provable Convergence and Certified Bounds
Model-Targeted Poisoning Attacks:Provable Convergence and Certified Bounds
“以模型为目标的投毒攻击:可证明收敛性和确定有界性”
written by : Fnu Suya ∗ Saeed Mahloujifar ∗ David Evans Yuan Tian
abstract
本篇文章主要研究了以特定分类器为目标的攻击者如何使用尽可能少的恶意样本(poisoning points)去诱导一个与该目标相近的分类器。提出了一个有效的在线凸优化方法以实现该攻击。对于任意可进行攻击的目标分类器,本篇文章证明了攻击的可收敛性(诱导模型到目标分类器所需的投毒点数),即诱导分类器与目标分类器的距离(相似度)与样本点数的平方根呈现负相关性。同时,本篇文章给出了最小恶意样本数的可证下界。实验表明,这种攻击性能等同甚至优于当时最优的攻击,拥有可证明的收敛性等优点,并且在在线攻击中,可以逐步确定最佳的投毒样本集。
introduction
训练机器学习模型通常需要大量标注样本,而这些样本又基本是从不可信的数据源收集而来。这就会带来许多安全问题,数据投毒就是其中之一。
本文将投毒攻击分为objective-driven attacks(对象驱动攻击)和model-targeted attacks(针对模型的攻击)。
前者仅针对某一对象xt进行攻击,即仅造成xt被错误分类。具体可以分为:(1)(不加区分的)任意攻击:降低模型的整体精度,模型会对任意一样本进行错误分类。 (2)针对特定实例的攻击:对某一特定xt进行错误分类。 (3)子种群攻击(最近提出的更现实的攻击):提高模型的错误率,或者对样本分布中预先定义的子种群进行错误分类。
由于上述攻击针对某一具体实例,故很难有统一的攻击方法。最常用的是基于梯度的局部优化器,虽然这种攻击方式经过修改后可被用于攻击另一目标,但其表现仍是糟糕的。为解决局部优化的局限性,有研究将攻击(1)归结为极大-极小优化问题,并使用在线凸优化有效解决了该问题,但该攻击也仅对任意攻击有效。
针对模型的攻击将目标合并至模型中(模型可以反映任意目标)。因此,只要找到合适的目标模型,就可以直接将相同的以模型为目标的攻击方法应用于一系列的任意攻击和子种群攻击。Koh等人提出了KKT attack,该攻击将复杂的双层优化转换为一个简单的凸优化问题,同时避免了局部优化。但这种攻击仅对一类特殊的损失函数有效,且对收敛性没有任何保证。本文的工作针对以模型为目标的攻击,探究了对任意目标模型进行投毒攻击的可行性,实验发现,针对某一特定分类器,理论和经验的投毒点界限是接近的。
contribution
1.提出了一个一般性的针对模型的投毒攻击策略,并用它确定了达到目标模型所需的投毒点数的下界。
2.以一种在线优化的方式工作,可以逐步找到接近最优的投毒点集,并证明了投毒所需最小数目的下界,该下界适用于所有损失函数(对于凸损失函数,可以求精确解;非凸,可求近似解)。
注:本文区别于其他的在线学习投毒机制,在后者的攻击中训练数据以流方式到达,而本文中训练数据以增量的方式变化,每次用于模型训练的数据集是固定的。
Comparison to KKT attack
1.可证的收敛性 2.适用于更广泛的凸损失函数族 3.在线攻击,无需提前知道投毒样本点数,故在增量投毒攻击中有效。4.实验结果表明,本文提出的攻击方法在子种群攻击中,比KKT有更好的性能;在任意攻击中,表现出相同的性能。
问题建立的条件
定义二元分类预测任务 h:X -> Y , X ∈Rd, Y = { +1,-1} ,h是经参数θ∈Θ ⊆Rd训练后的预测模型。这里不慌,给出其他条件时,也适用于多元分类预测或回归分析。
定义单点(x,y)上的非负凸损失函数 l(θ;x,y)
定义点集A上的经验损失L(θ;A) = Σ(x,y)∈Al(θ;x,y)
在X × Y 上假设一个真实数据分布 p*
博弈论方法展示投毒过程:
1. 从p*中均匀随机抽取N个数据点,构成干净训练集Dc。
2. 对手利用Dc、模型训练过程和模型空间Θ,生成一个满足攻击目标的目标分类器θp。(对应目标分类器生成过程,使用启发式生成方法)
3. 对手利用Dc、模型训练过程和模型空间Θ和θp生成一组中毒点Dp。(对应投毒攻击,最重要的步骤!!!)
4. 模型构建器在Dc∪Dp上训练模型,生成一个分类器θatk。(训练过程应该使结构的经验风险最小化)
对手的目标是使θatk尽可能接近θp,这里我们假设攻击者已知步骤(4)的过程:
![]()
R(θ)是正则化函数,CR为其系数。
解读:(1)我们假设对手拥有模型全知识 (2)仅向训练集中加入中毒点而非修改数据,虽然修改训练集造成的攻击更强但并不现实 (3)对于中毒点没有任何限制
Poisoning Attack with a Target Model
1. Model-Targeted Poisoning with Online Learning

如算法所示,本文的最终目标是使θt(算法产生的中间模型)与θp(算法的目标模型)的损失分布尽可能相似。
算法过程描述如下:首先,攻击者在第一次迭代中用Dc∪Dp(此时Dp为空集)训练中间模型θt。然后,开始寻找使θt和θp之间的损失差异最大化的点并加入到Dp中。重复整个过程,直到第2行满足stop条件(该条件可以灵活设置:1)对手对中毒点的预算为T,即算法运行T次 2)θt和θp之间的最大损失差异小于预设阈值ε 3)满足对手预先设定的精度要求。)本实验采用第二个停止条件。
对于训练量较大的模型,上述算法可能较慢,但其实这并不是问题。(1)算法第三行对应着一个在线优化过程,通常使用非常有效的在线梯度下降算法解决这个问题。(2)算法第四行每次仅向Dp加入一个点,实际上可以加入多个点。
2.Convergence of Our Poisoning Attack
如何证明本实验的攻击方法可以收敛呢?在这里,定义了基于损失的距离:
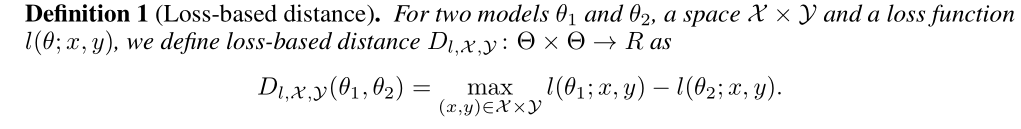
本文认为这个概念抓住了两个模型之间的“行为”距离。也就是说,θt和θp在所有点上的损失几乎相同,这意味着它们在所有空间中几乎具有相同的行为。注意,这里对距离的定义没有对称性的,因此它不是一个度规。对于某个可以获得的模型来说,任何模型都不可能与它有负的距离。基于这个距离,使用下面的定理证明算法的可收敛性:
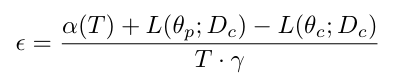
α(T) -> 由正则化因子CR确定的常数,与O(logT同阶) γ ->当损失函数是凸的,该在线算法的后悔(在线学习的每一轮误差与批量学习的误差的差距叫做后悔)
于是有当R(θ)是强凸的,ε ≤ O(logT / T),即当T ->∞, ε ->0,即该算法是收敛的。
该定理说明,θt和θp基于损失的距离与θp和θc之间的距离呈正相关,与中毒点的数量负相关点。也就是说,如果目标分类器θp越接近θc,则更容易实现攻击。另一方面,中毒点越多,使得θt越接近目标分类器,攻击就越有效。该定理证明了启发式方法的动机,即我们可以选择一个相对在干净数据上损失较小的θp。
3.Certified Lower Bound on the Number of poisoning Points
本文第一次证明了中毒点数的下界值,并且这个下界值可以用在我们的攻击算法中,得到实际值。定理如下:

该定理背后的直觉是,当添加到干净训练集的中毒点数量小于我们证明出的下界时,总存在一个比θp损失更小的分类器θ,因此无法实现投毒目标分类器。
此处要得到实际的下界值,只需将θ替换为一个已知的分类器即可,例如在Dc上训练的θc。我们的定理也适用于非凸函数。当然,为了找到非凸情况下损失差值最大的点,可以利用凸函数来确定损失差值的上界,并有效地计算出保守下界。
将这个公式并入算法中,只需要检查攻击过程中产生的所有中间分类器θt,并用θt 带入θ中进行计算。只要分子大于0,可计算出对应于θp和θt的下界。算法可以产生一个额外的下界并返回,且返回的是中毒过程中计算出的最高下界。
Experiments
数据集:the Adult dataset(k-means算法定义数据集的子种群 k=20,因为子种群攻击在现实中更受关注,所以最终选择实现子种群攻击)
模型:线性SVM
comparison:KKT攻击
输入:目标分类器,原始训练集 输出:一组中毒点
注:KKT需要一个固定的中毒点数量,而本文提出的攻击无需提前知道这个数量,但需要给出ε。所以先进行本文的攻击,将得到的数量np作为KKT的输入。
本文的攻击 : ε = 0.01 KKT: n = 0.2np, 0.4np, 0.6np, 0.8np, np
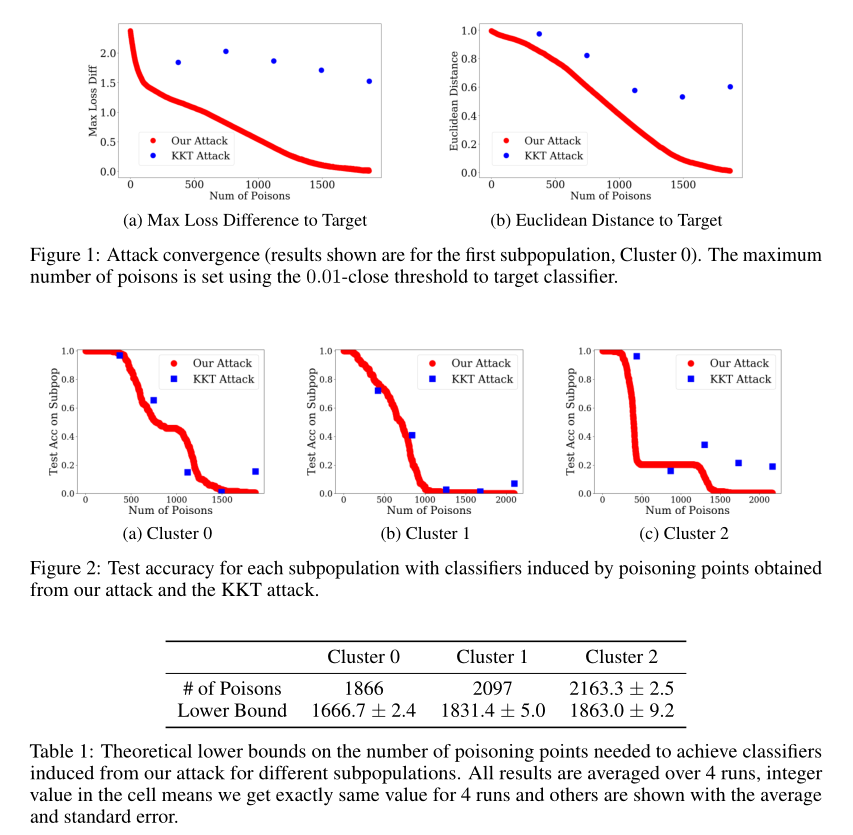
上图分别从收敛性、攻击成功率比较了两个实验。并给出了实际下界和计算下界的比较。
Conclusion
本文一个通用的中毒框架,证明了攻击成功任何可获得的目标分类器的收敛性,以及所需中毒点数量的下界。它首先获得目标模型,关注攻击的威力(中毒点的分布)来诱导模型。该框架也适用于先删除点,然后再向训练集添加新点的情况。
防御方面,可以考虑限制最大损失差点的搜索空间,以此来增加所需的中毒点的数量。
局限性方面,需要使用不同的凸损失函数以有效地搜索其“基于损失的距离”最大值,这并不包括一些常用的其他损失函数,如logistic损失。但本文提出的仍然可能是有效的(可以尝试在使用局部优化技术解决该问题)。
最后需说明的是,本文提出的攻击收敛性适用于任何有界的凸损失函数,而不依赖于损失差是否为凸。




