AI --> CNN（卷积神经网络）

本文学习了YouTube上的一个视频！！！

最近在学习使用pytorch框架，涉及到神经网络的定义和构建，此篇用于理解CNN~  

Youtube上最受欢迎的卷积神经网络科普视频： How Convolutional Neural Networks work（https://www.youtube.com/watch?v=FmpDIaiMIeA）

 

CNN的结构一般包含以下几层：

　　• 输入层：用于数据的输入

　　• 卷积层：使用卷积核进行特征提取和特征映射 

　　• 激励层：由于卷积也是一种线性运算，因此需要增加非线性映射

　　• 池化层：进行下采样，对特征图稀疏处理，减少数据运算量。

　　• 全连接层：通常在CNN的尾部进行重新拟合，减少特征信息的损失

 

卷积层负责提取图像中的局部特征；池化层用来大幅降低参数量级(降维)；全连接层类似传统神经网络的部分，用来输出想要的结果。

 

它通常用于计算机视觉方向，当然只要数据可以变成图像格式，也可用于其他领域！

 

以上图为例，CNN的目的其实就是破解这个识别的过程（可以看做一个黑盒~）！输入是图片，输出是对于图片的识别，即分类结果。

对于人来说，识别一个图像并进行分类是很容易的。但是对于计算机来说，我们输入的信号都只是数字信号，那么如何提取数字信号中的特征？

右面的这个图是原图经过旋转得到的，那么计算机应该如何识别它和原图的关系嘞？这就涉及到寻找图像的特征啦！

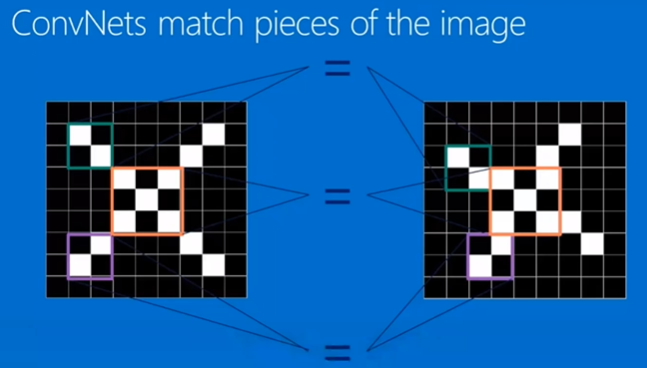
 我们会发现经过旋转得到的图片依然保留了原图的一些特征（上面用不同颜色圈出来的部分~）。那么我们就可以通过识别出这些特征，找出它和原图之间的相似性！

而上述这些特征，就是CNN中的卷积核（也叫特征提取器）！

 

那么一个卷积神经网络，需要有哪些操作？

一、卷积运算

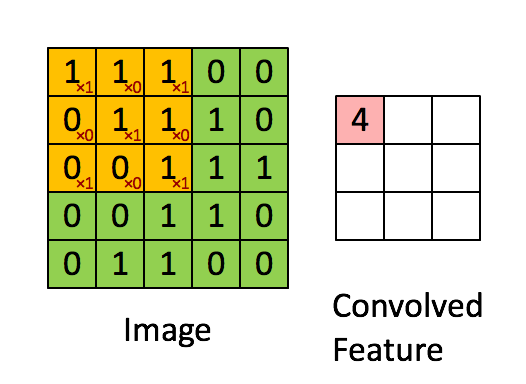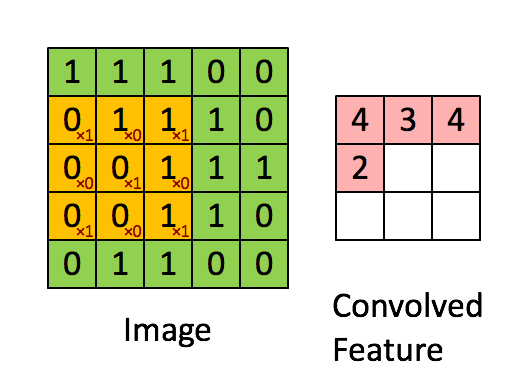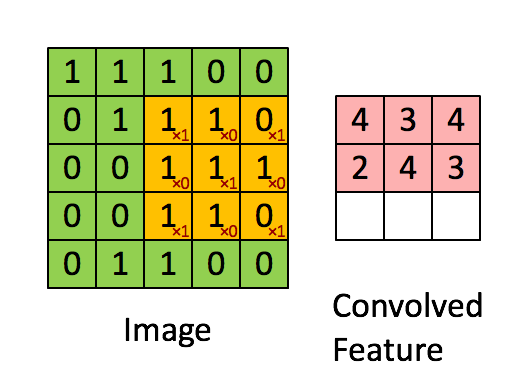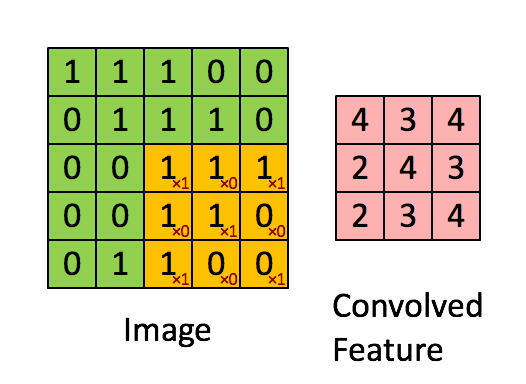
原图上的每一个值都和滑动的卷积核进行先乘积后加和的运算，得到的结果显示在一个新的矩阵（feature map）。当然之后也可以进行取平均值操作~

 

  

 

 

 

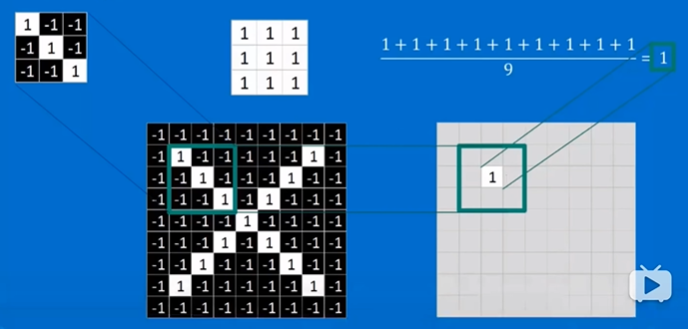
当值为1时，表示框出来的部分和卷积核特征完全一致。

 

 

 当取其他部分与卷积核进行运算时，不完全一致的结果<1。

 

 

 最终得到的结果如上图所示，我们发现这也是一个亮处在从左上到右下的对角线上，这表示原图中包含该卷积核对应特征的部分（值为1）被此卷积核提取了出来，结果保存在feature map中！！！

 

 

 三个卷积核分别进行卷积运算得到的结果如上~

哈哈哈哈，此时我们会想到，如果用其他的图片与这三个卷积核进行卷积，得到的结果会是什么样子呢？应该为混乱的结果，因为其他图片中可能并不包含这3个卷积核对应的特征。

当然，一个神经元可能不仅对图片的像素是否有着色（二值化后的黑色）敏感，可能还对图形的深度敏感。图形深度，是RGB颜色的值的深度量化，即对在计算机颜色处理中常用的红色Red，绿色Green，蓝色Blue进行参数化处理。     

一个三通道图片，使用两组卷积核，得到两个feature map！

那么，现实应用中，我们用到的卷积核可能非常非常多，对应的计算量也是相当巨大的，此时就需要缩小图像，这就涉及到我们接下来介绍的Pooling（池化），即下采样，它的作用是将得到的feature map进行缩小。

 

二、Pooling（池化）

    我们可以想到，数据量的减少，意味着会牺牲掉一部分信息，但是这是在我们可接受的范围内的。下面介绍两种池化方法：

1.Max Pooling：选取每个区域内最大的特征值代表整个区域。

2.Average Pooling：计算每个区域的平均值代表整个区域。

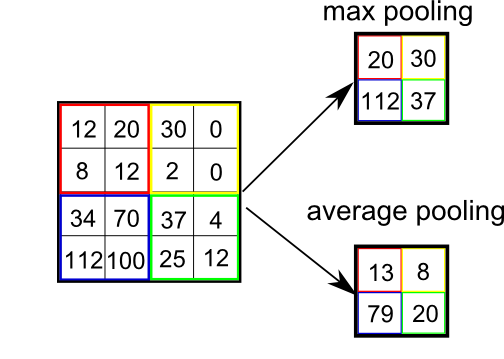
继续上面的例子~我们选用max pooling进行池化，得到如下结果（由于步长，可能导致池化过程对边缘进行补零[zero padding]后池化）：

 

 

 

 

 对三个feature map分别池化后的结果如上图所示，我们会发现依旧保留了这些特征。

 

三、激活函数

Rectified Linear Units(ReLus):修正线性单元激活函数 - >  对于feature map中的负值，全部变为0。这一步的目的是进一步简化运算，想想矩阵运算，0的参与会让计算更加快速！！！同时在进一步的梯度下降中，也会有很好的运算性能。

 

 

 

通过上面的图，我们可以看到原图经过卷积，激活函数，池化后的结果。而这三个步骤，其实就构成了一个简单的神经网络。它们也可以作为一个单元进行多次重复，如下面的这种操作：

 

 

 

四、全连接层

与之前的每一个神经元都相连，而每一个神经元都拥有自己的权重。  

         

 

中间经过重新排列的每一个值，都拥有一个权重。而这些权重是通过神经网络的训练得到的，嘿嘿！神经网络的奇妙之处~

 

 当然，全连接也可以有很多层~

 

综上，我们得到了如下图所示的完整的卷积神经网络！！！

 

 

反向传播

 那么，权重的值是如何获得的？卷积核又应该如何选择呢？这就需要我们对神经网络进行训练，每次训练后再对NN进行反向传播，即将每一次得到的结果与真实的结果进行比较，其实这也是损失函数的定义。如上图中， 识别该图片为X的可能性为0.92，代表有0.08的误差，识别该图片为O的可能性为0.51，代表有0.49的误差，损失函数值为0.57。

而我们需要做的，就是提供大量的数据，进行不断的训练，修改卷积核的参数，修改全连接层每一个神经元的权重，进行微调，使得损失函数降到最低，或者降至我们可接受的范围内。由于合格过程需要层层反馈，所以称之为反向传播。

如何使损失函数降到最低？？？

梯度下降算法：害，多维函数的导数，是时候该重新学数学了！

超参数

 虽然NN最终的参数由训练得到，但这些参数的初始值仍需要我们给出，即超参数~ 下面是一些常见的超参数：

 

 

而如何定义网络？隐藏层如何设计？全连接层需要多少神经元？这些问题都需要在今后的学习中逐渐探索，掌握经验！！！

此外，卷积神经网络还可以在处理视频、音频、文本等方面进行应用。注意，这些都是能呈现出类似图片结构的数据。而如果数据结构是表格方式，它们的列或行可以随机调换，而此时信息量并没有发生削减，那么无法应用CNN~

总之，卷积神经网络在挖掘特征、图像识别方面是非常好用的！还要继续努力学习鸭~

 

这里也推荐一篇知乎博文~ 俺这篇的两个动图源自下面奥！  

进一步理解卷积神经网络：https://zhuanlan.zhihu.com/p/49184702