PCA 实现原理及其在 Tennessee-Eastman 过程故障诊断中的应用
0 前言
为了提高系统的效率性、可靠性和安全性,一直以来,关于故障检测和分离的研究备受关注。作为过程工业的一部分,化工生产过程是经过化学反应将原料转变成产品的工艺过程。Tennessee-Eastman(TE) 过程是美国 Eastman 化学公司的 Downs & Vogel 于1993年建立的一个实际化工过程的模型,为研究该类过程的故障诊断技术提供了一个实验平台[1]。在生产过程中,一旦发生故障而又不能及时排除时,就会影响生产的进行,并威胁到人员和设备的安全,所以,需要准确及时地识别故障类型并进行相应的处理。目前,化工过程的故障诊断方法主要有模型驱动法和数据驱动法。由于化工过程往往具有慢时变、分布参数、非线性和强耦合特性,难以得到精确的数学模型,使得模型驱动方法的性能不尽理,因此,数据驱动的方法成为处理此类问题的一个重要方向。
在工业过程一类的复杂系统中,系统规模大且过程变量高度耦合,数学机理建模难,这为故障诊断带来了挑战。因而,基于数学机理建模的故障诊断方法不适用于复杂系统。在当前信息时代,系统中的过程数据很丰富且容易获取,从而数据驱动的方法被大量研究以及应用在复杂系统。其中,作为一种数据降维技术,主成分分析法(principal component analysis,PCA)能够提取过程数据中蕴含的强相关关系。PCA 广泛应用于复杂系统的故障诊断。如果检测的数据点大于 PCA 模型所定义的统计限,则判断该数据点为故障数据点,发出系统存在故障的报警。通常选取监控统计量 \(T^2\) 和 \(SPE\) 来进行故障诊断。这两个统计量分别是基于主成分得分和残差定义的。当 PCA 模型检测出故障时,迸一步实施故障分离,确定哪一个或哪几个变量是该故障的主要源头,称之为故障变量,从而帮助操作者根除故障源。通过假设故障变量对监控统计量具有最大的贡献,贡献图(contributionplots)常用于故障分离。本文以 TE 过程作为实验对象,应用基于 PCA 的故障诊断方法进行实验。
1 理论
本文接下来首先介绍 TE 过程的大致工业流程和数据结构,然后在介绍 PCA 的实现原理的基础上,给出基于 PCA 方法的故障诊断方法的实现方法步骤。
1.1 TE过程
Tennessee-Eastman(TE) 过程是 Downs 等人[1]基于 Tennessee Eastman 化学公司某实际化工生产过程提出的一个仿真系统,其具体流程见下图。在过程系统工程领域的研究中,TE 过程是一个常用的标准问题(benchmark problem),其较好地模拟了实际复杂工业过程系统的许多典型特征,因此被作为仿真例子广泛应用于控制、优化、过程监控与故障诊断的研究中。
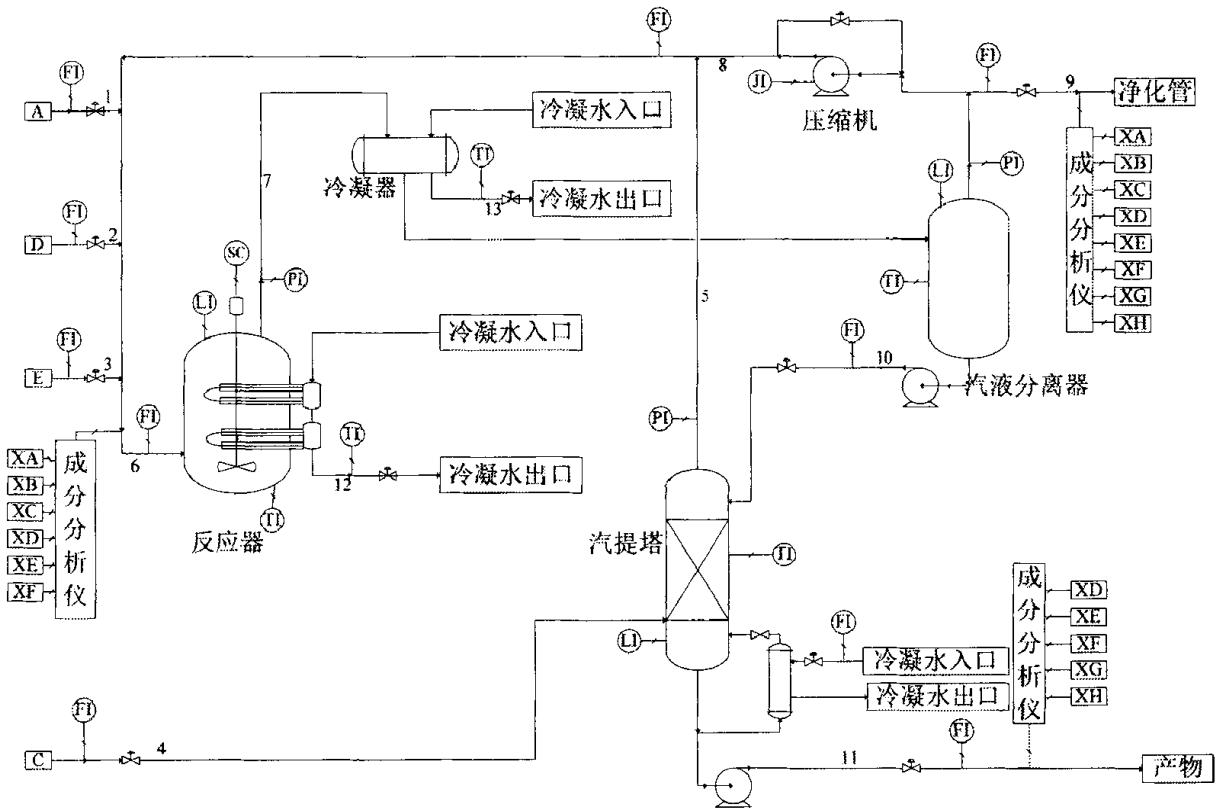
TE 过程包含四种气体原料 A、C、D 和 E,两种液态产物 G 和 H,还包含副产物 F 和惰性气体 B,其中进行的不可逆放热化学反应如下:
整个过程主要包含五个操作单元:反应器、冷凝器、循环压缩机、分离器和汽提塔。气态反应物进入反应器,生成液态产物,反应速率服从反应动力学中的 Arrhenius 函数。产物和残余反应物经过冷凝器冷却后进入汽液分离器,分离得到的气体通过压缩机进入循环管道,与新鲜进料混合送入反应器循环使用,分离得到的液体经过管道 10 进入汽提塔进行精制,从汽提塔底得到的流股中主要包含 TE 过程的产物 G 和 H,送至下游过程。TE 过程总共包括12 个操纵变量和 41 个测量变量(包含 22 个连续过程变量和 19 个成分变量),采用 Lyman 和 Georgakis [2] 提出的过程结构。
TE 过程模拟实际工业过程中常见的 21 种故障模式,这 21 种故障模式的具体描述如表 1 所示。本次实验采用的TE数据集由训练集和测试集组成,数据由 22 次不同的仿真运行数据构成,每个样本都有 53 个观测变量(取 52 个变量时,第 12 个操纵变量 XMV(12) 搅拌速度就不包括在内)。22 次仿真数据每次都分为了训练集样本和测试集样本。正常工况下的训练样本是在 25h 运行仿真下获得的,观测数据总数为 500,而测试样本是在 48h 运行仿真下获得的,观测数据总数为 960 。其余 21 次仿真数据为带有故障的训练集样本,同样分为训练样本和测试样本,每组训练样本\测试样本代表一种故障。带有故障的测试集样本在 48h 运行仿真下获得,其中前 160 个观测值为正常数据,故障在 8h 的时候引入,共采集 960 个观测值。
| 故障号 | 故障描述 | 类型 |
|---|---|---|
| 1 | A/C进料比值变化,B含量不变(管道4) | 阶跃 |
| 2 | B含量变化,A/C进料比值不变(管道4) | 阶跃 |
| 3 | D进料温度变化(管道2) | 阶跃 |
| 4 | 反应器冷却水入口温度变化 | 阶跃 |
| 5 | 冷凝器冷却水入口温度变化 | 阶跃 |
| 6 | A供给量损失(管道1) | 阶跃 |
| 7 | c供给管压力头损失(管道4) | 阶跃 |
| 8 | A,B,C供给量变化(管道4) | 随机 |
| 9 | D进料温度变化(管道2) | 随机 |
| 10 | C进料温度变化(管道2) | 随机 |
| 11 | 反应器冷却水入口温度变化 | 随机 |
| 12 | 冷凝器冷却水入口温度 | 随机 |
| 13 | 反应动力学参数 | 缓慢漂移 |
| 14 | 反应器冷却水阀 | 阀粘滞 |
| 15 | 冷凝器冷却水阀 | 阀粘滞 |
| 16 | D进料温度变化(管道2) | 未知 |
| 17 | 未知 | 未知 |
| 18 | 未知 | 未知 |
| 19 | 未知 | 未知 |
| 20 | 未知 | 未知 |
| 21 | 阀门位置(管道4) | 卡阀 |
1.2 主成分分析
主成分分析(PCA)法也叫主元分析法,是一种数据降维算法,降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。在实际的生产和应用中,降维在一定的信息损失范围内,可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。降维具有的优点有:使得数据集更易使用、降低算法的计算开销、去除噪声、使得结果容易理解。而 PCA 是一种使用最广泛的数据降维算法。
PCA 的主要思想是将 \(n\) 维特征映射到 \(k\) 维空间中,这里的必有 \(k<n\),在原有 \(n\) 维特征的基础上重新构造出来的全新的 \(k\) 维特征数据具有正交特性,也被称为主成分或主元。PCA 的工作就是从原始的高维空间中,根据方差大小顺序地找出一组相互正交的坐标轴,所以新的坐标轴的选择与原始数据密切相关。第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取与第一个坐标轴正交的超平面中使得方差最大的方向,第三个轴是与第 1、2 个轴正交的超平面中方差最大的,依次类推,可以得到n个这样的坐标轴。获得的新坐标系中我们可以发现,绝大部分方差较大的方向都包含在前面 \(k\) 个坐标轴中,其后的坐标轴所含对应的方差权重远小于前 \(k\) 维坐标,于是只保留前面 \(k\) 个含有绝大部分方差的坐标轴。这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为 0 的特征维度,实现对数据特征的降维处理。
从以上描述我们知道得到这些包含最大差异性的主成分方向的方法,就是通过计算数据矩阵的协方差矩阵,然后得到协方差矩阵的特征值特征向量,选择特征值最大(即方差最大)的 \(k\) 个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中,实现数据特征的降维。由于得到协方差矩阵的特征值特征向量有两种方法:特征值分解协方差矩阵、奇异值分解协方差矩阵,所以 PCA 算法有两种实现方法:基于特征值分解协方差矩阵实现和基于 SVD 分解协方差矩阵实现。下面从最大化方差的角度简单推导 PCA 的实现原理,并给出基于特征值分解的算法步骤。
假设有一组数据包含 \(m\) 个样本,每个样本 \(\boldsymbol{x_i}\in \mathbb{R}^n\),
现在假设使用一个 \(\boldsymbol{P}\) 矩阵对样本进行降维,
变换得到降维后的数据矩阵 \(\boldsymbol{Y}\),其中 \(\boldsymbol{y_i}\in\mathbb{R}^k, k < n\),
所以变换矩阵 \(\boldsymbol{P}\) 就是,
每一个 \(\boldsymbol{p}_i\) 同 \(\boldsymbol{x_i}\) 一样是 \(n\) 维向量,那么得到这些向量就得到了 \(\boldsymbol{P}\) 矩阵。且因为由于是每一个向量与样本进行点积的总和,所以我们应该是出于同样的理由来确定每一个 \(\boldsymbol{p}_i\)。我们可以将每一个 \(\boldsymbol{p}_i\) 单位化,即使得 \(\boldsymbol{p^T}\boldsymbol{p}=1\),就可以把内积 \(\boldsymbol{p}\cdot \boldsymbol{x}\) 看做是 \(\boldsymbol{x}\) 在 \(\boldsymbol{p}\) 方向上的投影,
那么为了投影过后的样本点在投影方向上最大可能地保留原本的信息,就要让投影点尽可能地散开,而散开的程度可以用方差来描述,所以只需要求得使方差最大的一组方向,那么矩阵 \(\boldsymbol{P}\) 中的向量就是在这些方向上的单位向量。
首先求原始样本的协方差矩阵,
其中 \(\boldsymbol{\bar{x}}\) 是样本均值,
则样本点在 \(\boldsymbol{p}\) 向量所在方向上的投影的方差 \(\sigma^2\) 可以由式 \(\eqref{eq:variance}\) 表示,
其中,\(\mu = 1/m\sum_{i=1}^m{\boldsymbol{p^T}\boldsymbol{x_i}}\),经过如下的推导过程,
由此得到如式 \(\eqref{eq:variance2}\) 的关系,
现在我们要求的 \(\boldsymbol{p}\) 向量需要满足 \(\boldsymbol{\hat{p}}=\arg\underset{\boldsymbol{p}}{\max}{\boldsymbol{p^T \Sigma p}}\),同时满足前面所提的约束条件 \(\boldsymbol{p^T p}=1\),那么我们可以通过Lagrange乘数法构造一个目标函数如式(10),
让目标函数对 \(\boldsymbol{p}\) 求偏导,并令偏导为零,得到,
由此可以看出,投影后的方差就是协方差矩阵的特征值。\(\Sigma\) 是一个对称矩阵,可以做如下特征分解,
其中 \(\boldsymbol{C}\) 是一个 \(n \times n\) 的矩阵,并且是一个正交矩阵,即 \(\boldsymbol{C^T C}=\boldsymbol{E}\)。它就是由 \(\Sigma\) 的所有特征向量组成的,
前面说过,为了让投影后的方差最大,我们需要选取 \(\Sigma\) 前 \(k\) 个最大的特征值对应的特征向量组成变换矩阵 \(\boldsymbol{P}=\begin{pmatrix}\boldsymbol{p_1}\,\boldsymbol{p_2}\cdots\boldsymbol{p_k}\end{pmatrix},\ k<n\),从而得到降维后的数据集 \(\boldsymbol{Y}\),满足的关系如下
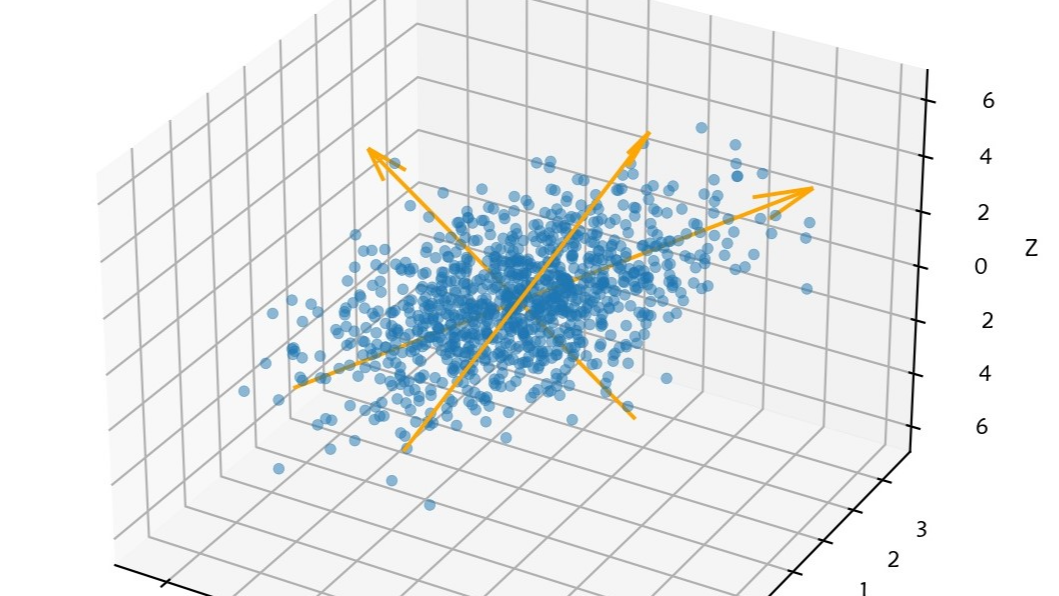
用三维变量的观测数据举例,如下图所示,在三维空间中来看,这一变换的过程就是将原坐标空间变换到以特征向量方向(图中三个箭头所指的方向)为坐标轴的新空间中。
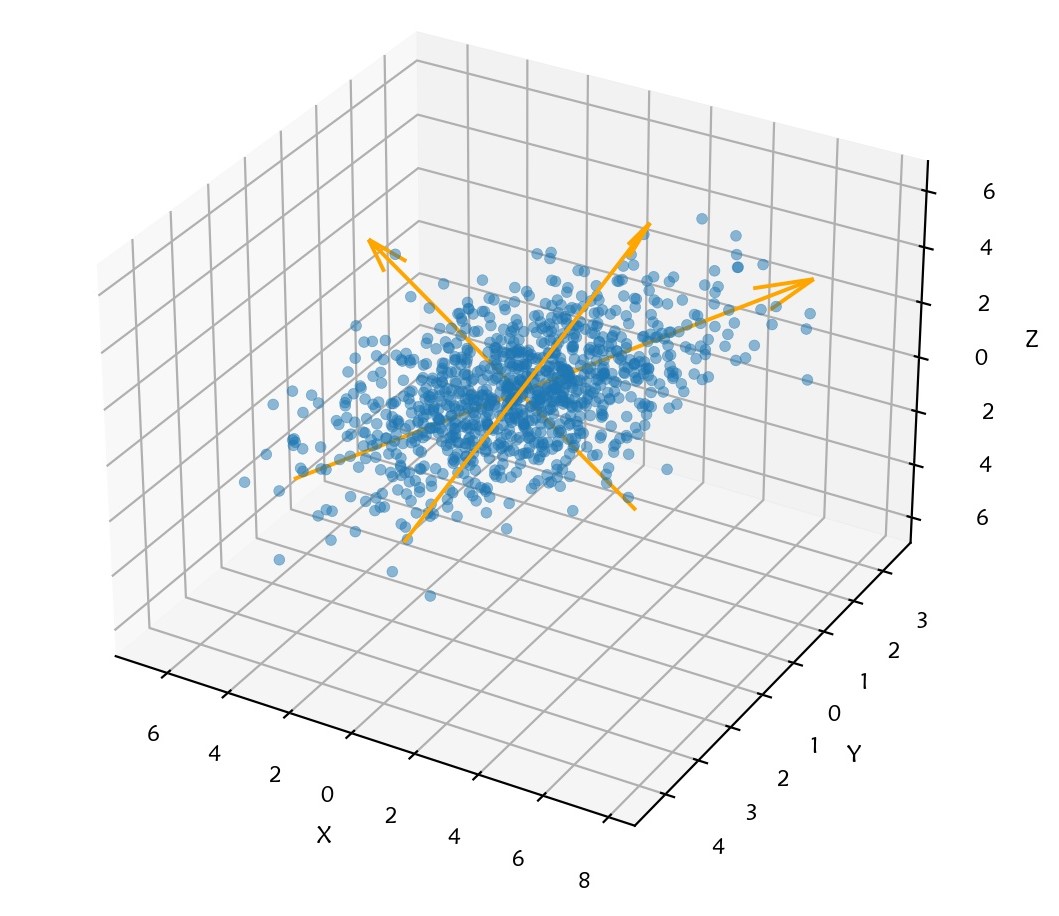
主元分析中需要注意的两点是:数据的标准化和主元个数的选取问题。对于数据的标准化问题,原始数据矩阵 \(X_{m\times n}\) 每一列对应于一个测量维度,每一行对应一个样本。两个样本间的相似度应正比于两个样本点在 \(n\) 维空间中的接近程度,由于 \(n\) 个观测变量的量纲和变化幅度不同,其绝对值大小可能相差许多倍。为了消除量纲和变化幅度不同带来的影响,原始建模数据应作标准化处理,
其中,\(\boldsymbol{\bar{x}_j}=1/m\sum_{i=1}^m{\boldsymbol{x}_{ij}}\) 是第 \(j\) 维上的数据均值,\(\boldsymbol{s_j}=\sqrt{1/(m-1)\sum_{i=1}^m{\left(\boldsymbol{x}_{ij}-\boldsymbol{\bar{x}_j}\right)^2}}\) 为第 \(j\) 维上的数据标准差,测试数据也要按照原始变量的均值和标准差进行标准化处理。
对于主元个数选取问题,应考虑两个方面的因素:即原始观测数据维数的降低和原始观测数据信息的丢失。主元个数的选取直接影响到故障监测与诊断的效果。如果主元数目选得过小,则残差子空间所包含的方差太多,使的残差子空间统计量的阈值偏大,从而导致小故障难于被检测出;而若主元数目取的太大,又会使残差子空间包含的信息太少,使得故障对残差影响不大,故障难于被监测出。可见,主元个数的选取是很重要的。通常,采用简单可行的累积方差百分比(cumulative percent variance,CPV)方法来确定选取的主元的个数 \(k\),前 \(k\) 个特征值之和除以所有特征值之和被称为前 \(k\) 个主元的累积方差贡献率,表示这 \(k\) 个主元所能够解释的数据方差的比例,即
通常选取 \(\alpha\) 为85%、90% 或 95%. 至此我们可以得到基于特征值分解的 PCA 算法步骤:
输入:数据集 \(\boldsymbol{X}_{m\times n}=(\boldsymbol{x_1},\boldsymbol{x_2}\cdots\boldsymbol{x_m})^T\),需要降到k维。
- 标准化,即每一维特征减去各自的平均值,再除以每一维的标准差;
- 计算协方差矩阵 \(\Sigma_{n\times n}=\boldsymbol{X^T X}/(m-1)\);
- 用特征值分解方法求协方差矩阵的特征值与特征向量;
- 对特征值从大到小排序,选择其中最大的 \(k\) 个,将其对应的 \(k\) 个特征向量分别组成降维矩阵 \(P\);
- 将数据转换到 \(k\) 个特征向量构建的低维子空间中,即 \(\boldsymbol{Y^T} = \boldsymbol{P^T X^T}\).
1.3 基于PCA的故障检测
为了方便描述,以下首先引入一些多元统计学中的定义。承接前面的条件,不妨假定维数 \(n=k+r\),\(k\) 表示最终保留的维数,\(r\) 则为剩下的维数,则可以进行如下变换:
其中 \(\boldsymbol{p_i}\in\mathbb{R}^n\) 为 \(\boldsymbol{x}\) 的协方差阵特征值 \(\lambda_i\) 对应的特征向量,且各特征值如下排列
\(\boldsymbol{p_i}\) 之间是相互正交的单位向量,\(t_i\) 称为第 \(i\) 主元,我们所关心的变量 \(\boldsymbol{x}\) 是一个 \(n\) 维向量,它的一组测量值 \(\boldsymbol{x}(\tau)\) 经过式 \(\eqref{eq:score}\) 变换后得到的值 \(t_i(\tau)\) 称为测量值在第 \(i\) 主元上的得分。主元代表的是变量,而得分是确定值,从几何上解释,主元可以看做是降维后的坐标轴,而得分就是原向量在坐标轴上对应的坐标值。向量 \(\boldsymbol{p_i}\) 被称为第 \(i\) 主元的负荷向量。
PCA 就是求取主元、得分及负荷向量的过程。我们把转换矩阵 \(\boldsymbol{P}\) 称为负荷矩阵,它所长成的 \(k\) 维子空间被称为主元子空间(Principal Component Subspace, PCS),又称模型子空间或表示子空间(Represent Subspace),\(\boldsymbol{T}=\boldsymbol{X P}\) 为由 \(k\) 列得分向量 \([t_i(1),t_i(2),\cdots,t_i(m)]^T\) 组成的矩阵称为得分矩阵,由前面推导结论可以知道,它就是所要求的 \(\boldsymbol{Y}\) 矩阵,只是从不同角度解释而已。后 \(r\) 个主元对应的负荷向量组成的矩阵用 \(\boldsymbol{\overline{P}}\) 表示,被称为残差负荷矩阵,它所张成的 \(r\) 维空间被称为残差子空间(Residual Subspace, RS),即是说 \(\boldsymbol{C}=\left(\boldsymbol{P,\overline{P}}\right)\)。我们可对观测数据矩阵做如下分解,
其中的 \(\boldsymbol{\widehat{X}}_{m\times n}\) 为观测数据矩阵 \(\boldsymbol{X}\) 在 PCS 上的估计或称分量,\(\boldsymbol{R}_{m\times n}\) 为观测数据在残差子空间上的分量,被称为模型的估计残差矩阵。由此可知,通过对正常数据阵 \(\boldsymbol{X}\) 进行 PCA,可以把我们所关心的变量 \(\boldsymbol{x}\) 的观测数据分解为两个子空间的数据,
故障检测就是检测系统中各个监测点的数据有无异常,它通常是将新的观测数据 \(\boldsymbol{x}_{new}\) 与系统校验模型相比较来实现的。跟据两者之间差距的显著性程度,判断系统中有无故障。主元分析法将数据空间分解为主元子空间和残差子空间,每一组观测数据都可以投影到这两个子空间内。因此引入 Hotelling \(T^2\) 和平方预报误差(Squared Prediction Error, SPE)这两个统计量来监测故障的发生。Hotelling \(T^2\) 统计量是用来衡量包含在主元模型中的信息大小,它表示标准分值平方和。它的定义如下,
系统如果正常运行,则 \(T^2\) 应满足
其中,\(T_\alpha\) 为 \(T^2\) 的控制限,\(k\) 为保留的主元数,\(m\) 为样本数,\(1-\alpha\) 是置信度,\(F_\alpha(k, m-k)\) 是服从第一自由度为 \(k\),第二自由度为 \(m-k\) 的 \(F\) 分布。\(\alpha\) 满足概率公式 \(P\left\{F(m_1,m_2)>F_\alpha(m_1,m_2)\right\}=\alpha\),在此定义下,\(\alpha\) 取值通常较小的值,如 0.01 左右。
\(SPE\) 统计量也称 \(Q\) 统计量,是通过分析新的观测数据 \(\boldsymbol{x}_{new}\) 的残差进行故障诊断,用以表明这个采样数据在多大程度上符合主元模型,它衡量了这个数据点不能被主元模型所描述的信息量的大小。它的计算如下,
\(SPE\) 的控制限计算公式为,
其中,
且 \(c_\alpha\) 是标准正态分布的置信极限,满足 \(P\{N(0,1)>N_{c_\alpha}(0,1)\}=c_\alpha\),在此定义下 \(\alpha\) 取值通常也取 0.01 左右。如系统正常运行,则样本的 \(SPE\) 值应该满足 \(SPE<Q_\alpha\).
在基于 PCA 的故障检测中,对于这两种统计量会会出现四种情况:
-
\(T^2\) 和 \(SPE\) 统计量都不超过控制限;
-
\(T^2\) 正常,但 \(SPE\) 超出 \(Q_\alpha\);
-
\(T^2\) 超出 \(T_\alpha\),但 \(SPE\) 正常;
-
\(T^2\) 和 \(SPE\) 都超出控制限。
一般认为 2 和 4 为故障,另两种正常。
1.4. 基于PCA的故障隔离
当监控系统利用检测统计量检测到过程中发生异常后,应及时完成故障的定位与隔离(Fault Isolation),又称故障识别(Fault Identification)。这里介绍有两种实现故障的诊断的途径。
一种是将故障诊断看作是模式识别的过程,所以可以采用模式识别技术直接进行故障的诊断,在这里 PCA 是作为辅助工具在条件允许时实现对数据的降维。基于模式识别的故障诊断方法包括特征提取和故障识别两个主要步骤。第一步通过滤波消除数据信号的随机干扰影响,提取过程特征信息,包括各种故障信息;第二步通过构建有效的分类器,将新采样数据的过程特征同故障库中存在的过程特征进行匹配,实现故障的诊断。常采用的模式识别技术有动态时间规整(Dynamic Time Warping, DTW)、神经网络、支撑向量机等。但基于模式识别的故障诊断方法首先要实现过程特征的提取,这需要大量的先验知识和含有各种故障信息的历史数据,大大限制了该方法的应用。
另一种方法是利用基于 PCA 的技术把故障先定位到过程中某个部分或某个变量,实现故障的隔离,这样就大大减弱了对故障库的依赖,同时还对下一步故障诊断产生直接的指导作用,条件允许时还可以直接实现故障的诊断,在这类方法中,PCA 作为故障隔离的主要工具。贡献图是这类方法中的一种比较基础的方法,一旦检测到系统发生故障,则根据变量方差贡献初步确定与故障关联较紧密的若干变量或子系统,从而实现故障的定位与隔离。贡献图给出了被监控的各个过程变量对检测统计量(一般为 \(T^2\) 或 \(SPE\))的贡献,它较易生成,不需要先验过程知识。该法的理论基础是假设高贡献率的过程变量是故障产生的原因,但是由于一个变量故障会影响到其它变量在主元模型下的估计值,进而影响到这些变量对检测统计量的贡献,所以贡献图只能为操作员提供一定程度的指示作用。本文的实验以贡献图作为故障隔离的方法,下面给出计算过程:
当有异常状态发生时,绘制贡献图,找出与故障相关的系统变量:
-
检查每个观测向量 \(\boldsymbol{x}\) 的标准化得分 \(t_i/\lambda_i\),并确定造成失控状态的 \(u\) 个得分(\(u<k\)),按下式确定,
\[\frac{t_i}{\lambda_i} < \frac{T_\alpha}{k} \] -
计算观测向量 \(\boldsymbol{x}\) 的每个分量值 \(x_j\) 相对于失控得分 \(t_{s_i}\) 的贡献率,按下式计算,注意下标 \(s_i\) 有 \(u\) 个而不是 \(k\) 个,它是第 1 步中确定出的 \(u\) 个得分的下标,而不是从 1 顺序递增的值,
\[cont_{s_ij} = \frac{t_{s_i}}{\lambda_{s_i}}p_{s_ij}x_j,\ i\in[1,u],s_i\in[i,k],j\in[1,n] \] -
当 \(cont_{s_ij}\)是负时,设为零,
-
分别计算每个过程分量的总贡献率,第 \(j\) 个过程分量 \(x_j\) 的总贡献率为
\[cont_j = \sum_{i=1}^u {cont_{s_ij}} \] -
把所有 \(n\) 个过程分量的总贡献率画在一个直方图中。
2 实验
本次实验所用到的数据集只是全部 TE 数据集的一部分。TE过程数据集中的 22 个仿真数据集,包括 1 个正常数据集,21 个故障数据集,每个故障数据集对应一个故障模式,每个数据集都包括了 960 个采样点,过程变量采样间隔为 3 分钟,成分变量的采样间隔为 6-15 分钟。在这 21 种故障模式中,过程起初都运行在正常模式下,在第 60 个采样点时,发生了故障,故障一旦发生并持续到了过程结束。本次实验采用了 52 个观测变量,使用正常数据集中的训练数据建立 PCA 模型,计算 \(T_\alpha\) 和 \(Q_\alpha\) 控制限,使用 21 个故障数据集中的测试集进行故障测试与隔离实验。
2.1 实验过程
基于 PCA 方法的在TE过程案例的故障诊断实验流程如下图所示。首先输入正常数据集中的训练集,数据规模为 \(500\times20\)。对数据标准化之后,进行 PCA 模型的建立,在建立 PCA 模型过程中,采用 90% 的 CPV 方法选取主元数目,在得到负荷矩阵 \(\boldsymbol{P}\) 以及 \(T^2\) 和 \(SPE\) 两种统计量的控制限之后,对故障数据集中测试集分别进行故障检测与故障隔离实验。
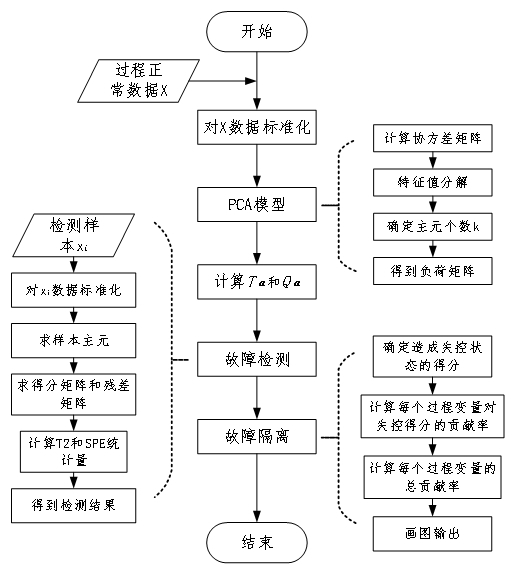
每种故障测试集的数据规模是 \(960\times52\),在进行故障检测时,使用建立 PCA 模型中得到负荷矩阵求取主元,而实际上得分矩阵和残差矩阵的计算和两种统计量的计算在可以直接通过式 \(\eqref{eq:T2}\) 和式 \(\eqref{eq:SPE}\) 在同一步骤进行计算,通过统计量与控制限的比较,判断故障是否发生,当发生故障时,通过求贡献图的方式发现故障发生的可能原因,以实现故障的定位与隔离。实验代码(matlab)见文末。
2.2 结果分析
基于 PCA 的21种故障诊断结果如下表所示,表中粗体显示每种故障模式下两种统计量评判的最低故障漏报率、最低故障误报率与最少延迟诊断时间。由于在故障模式 3、9 和 15 中过程变量数据的均值和方差均受故障影响不大,所以这三种故障难以被检测出。从表中还可以看出,\(T^2\) 的总体误报率要低于 \(SPE\) 统计量,而对于漏报率和延迟诊断时间上 \(SPE\) 相对有较大的优势。所以在故障检测过程中,可以综合两者的评判结果做出判断,以得到更加准确的检测结果。单独从延迟诊断时间来看,基于 PCA 模型的故障诊断方法对阶跃型的故障信号具有较高的敏感性,而对其他如随机型的、阀粘滞型的或者未知类型的故障信号敏感性较弱。
| 故障号 | \(T^2\) 误报率 / 漏报率(%) / 延迟诊断时间(T) | \(SPE\) 误报率(%) / 漏报率(%) / 延迟诊断时间(T) |
|---|---|---|
| 1 | 0.00 / 0.63 / 4 | 8.75 / 0.13 / 1 |
| 2 | 1.25 / 1.63 / 12 | 11.88 / 0.63 / 1 |
| 3 | 1.25 / 96.88 / 20 | 18.75 / 81.25 / 1 |
| 4 | 1.88 / 45.88 / 0 | 11.25 / 0.00 / 0 |
| 5 | 1.88 / 72.63 / 0 | 11.25 / 56.50 / 0 |
| 6 | 0.00 / 0.75 / 6 | 7.50 / 0.00 / 0 |
| 7 | 0.00 / 0.00 / 0 | 9.38 / 0.00 / 0 |
| 8 | 0.63 / 2.50 / 15 | 8.13 / 2.50 / 13 |
| 9 | 6.25 / 96.38 / 0 | 16.88 / 84.88 / 2 |
| 10 | 0.63 / 54.50 / 18 | 14.38 / 27.88 / 0 |
| 11 | 0.63 / 44.50 / 5 | 16.25 / 26.50 / 6 |
| 12 | 0.63 / 1.25 / 2 | 15.00 / 1.88 / 3 |
| 13 | 0.00 / 4.63 / 36 | 8.75 / 4.00 / 17 |
| 14 | 0.63 / 0.00 / 0 | 18.13 / 1.13 / 1 |
| 15 | 0.00 / 94.50 / 91 | 9.38 / 78.88 / 2 |
| 16 | 7.50 / 74.63 / 1 | 11.88 / 34.13 / 4 |
| 17 | 0.63 / 18.38 / 1 | 20.00 / 2.50 / 10 |
| 18 | 1.25 / 10.63 / 17 | 12.50 / 7.88 / 9 |
| 19 | 0.63 / 89.25 / 10 | 8.75 / 52.88 / 1 |
| 20 | 1.25 / 59.38 / 86 | 9.38 / 30.38 / 6 |
| 21 | 3.13 / 61.13 / 26 | 24.38 / 34.63 / 0 |
从表中还可以看出基于 PCA 模型的故障检测对TE过程的某些故障检测效果更佳(如对故障模式1、2、4、6、12、14、17、18),而对另外的故障情况的检测结果不理想,这也说明了基于PCA模型的故障检测具有局限性。
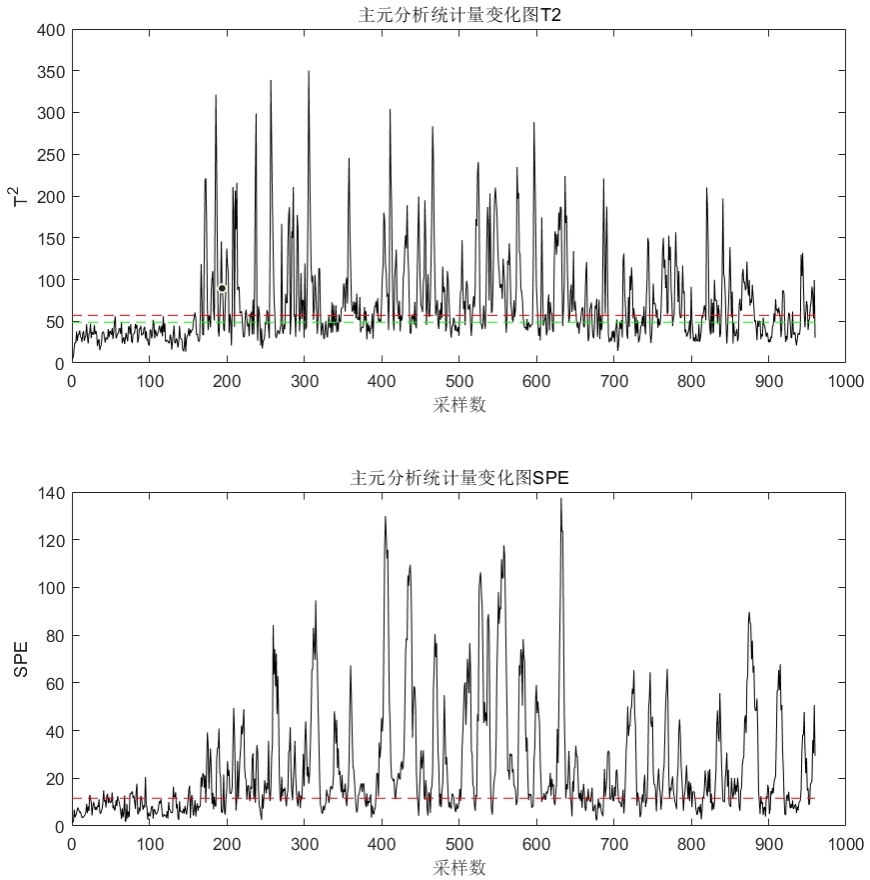
从检测波形和贡献图上来看可以得到与前述结论相似的结果。基于 PCA 模型的故障诊断对于某一些故障(如下图中的故障 14 )具有很好的检测和隔离效果。
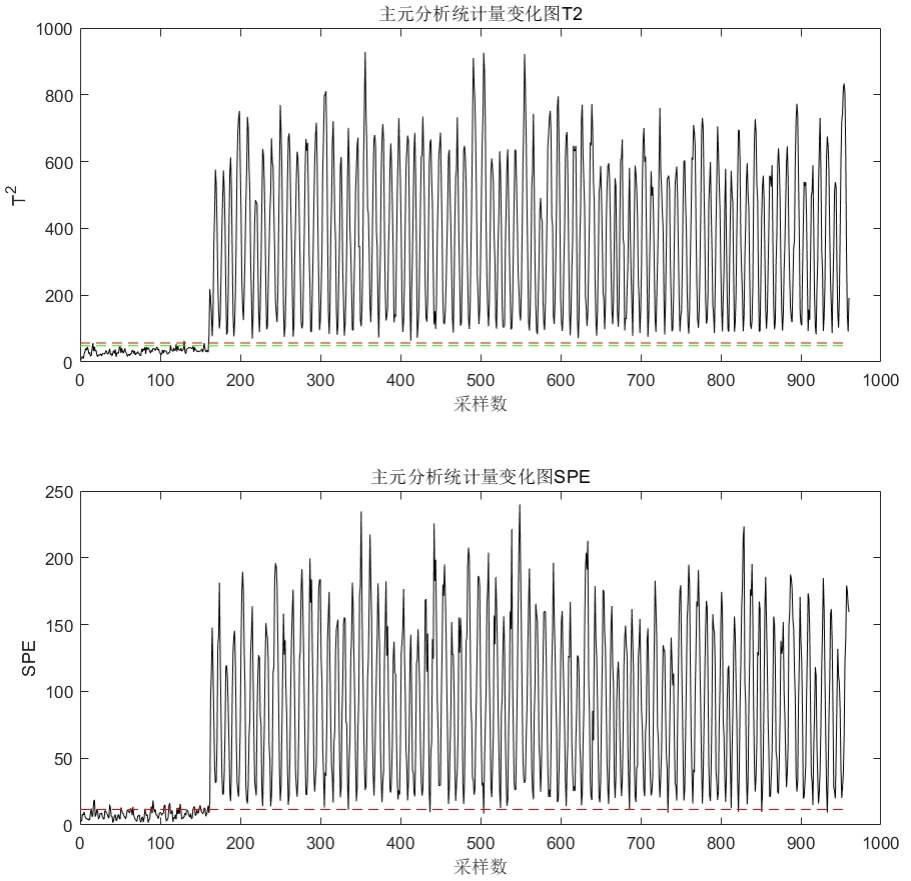
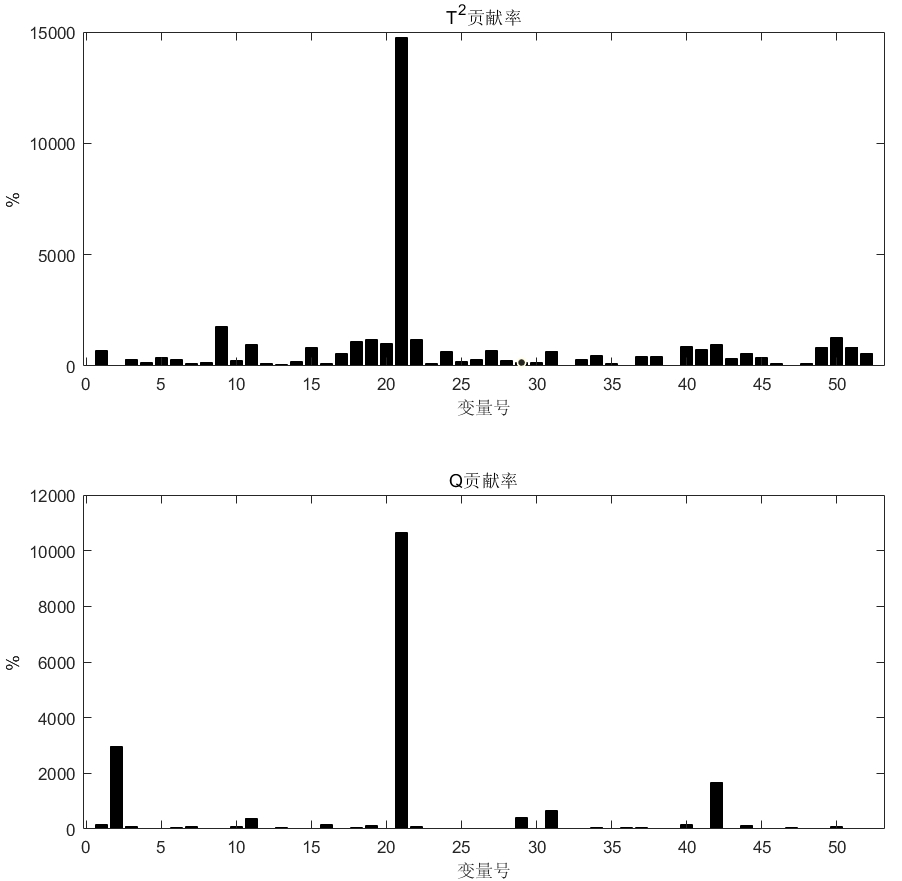
而对于某些故障模式,该方法有表现出不可靠的诊断效果,如下图所示中的对故障模式 9 的诊断结果。这也说明了该方法对随机故障信号的故障诊断效果不理想。

而从那些诊断效果较好的结果中可以看出,使用贡献图进行故障隔离时,使用 \(SPE\) 统计量计算的贡献率结果相较于 \(T^2\) 统计量的计算结果更具有参考意义,如下图中第一张图中所示,其计算出的 52 观测变量对于当前故障的贡献率大小区分度更为明显。
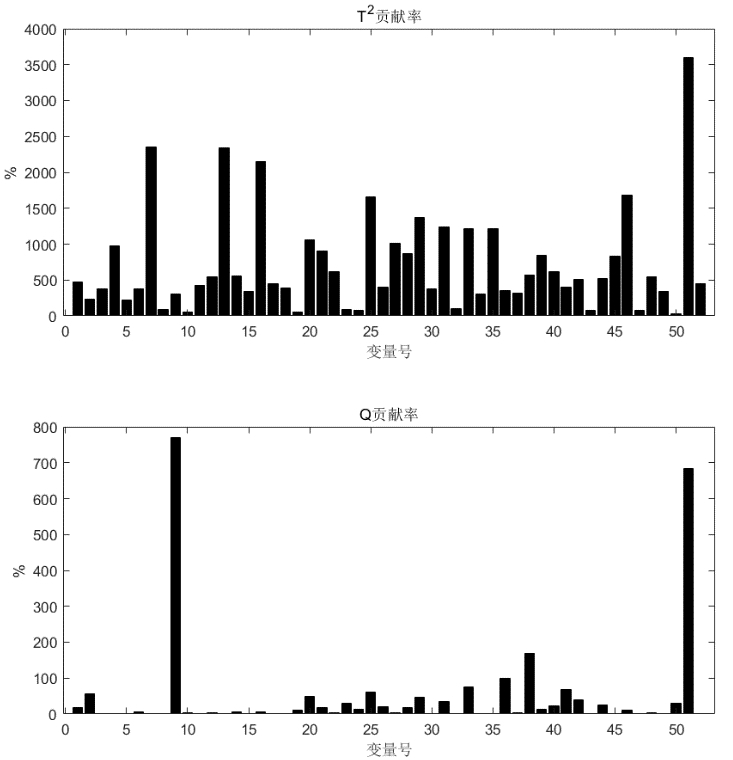
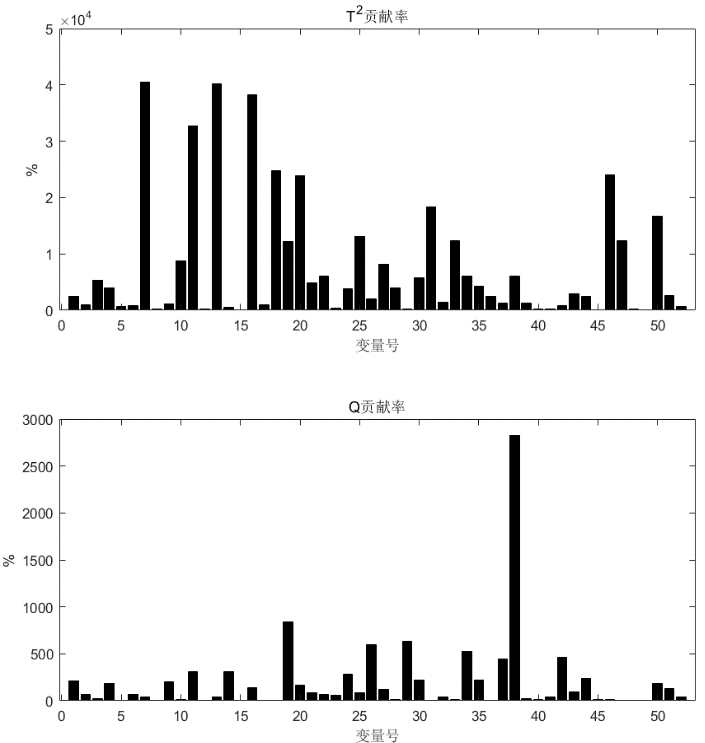
而基于贡献图的方法也被证明了具有很大局限性,Alcala 和 Qin[4] 证明贡献图对某些简单的传感器故障也不能保证得到正确的故障诊断结果,并为此提出了基于重构的贡献图方法(reconstruction based contribution,RBC)。更为本质的原因是像 PCA 这类的纯数据驱动方法无法描述过程的机理反应,所建的数据模型缺乏清晰的物理含义,相互之间的因果关系不明确,因此当应用在复杂系统中定位和诊断故障源时就造成了很大限制。同时基本的 PCA 模型没有考虑到很多更复杂的问题,如非线性问题、局部性问题、稀疏性问题、动态性问题、自适应问题等,这些实际应用中的问题也是其诊断效果十分局限的原因[7]。
实验代码
% 基于 PCA 模型的在 TE 过程中的故障诊断仿真实验
close all; clear; clc;
data=load('TE_data.mat');
data = struct2cell(data);
testdata = data(1:22);
train = cell2mat(data(23));
train = train';
train_mean = mean(train); %按列 Xtrain 平均值
train_std = std(train); %求标准差
[train_row,train_col] = size(train); %求 train 行、列数
train=(train-repmat(train_mean,train_row,1))./repmat(train_std,train_row,1); %标准化
sigmatrain = cov(train); %求协方差矩阵
%对协方差矩阵进行特征分解,lamda 为特征值构成的对角阵,T的列为单位特征向量,且与 lamda 中的特征值一一对应:
[T,lamda] = eig(sigmatrain);
%取对角元素(结果为一列向量),即 lamda 值,并上下反转使其从大到小排列,主元个数初值为 1,若累计贡献率小于90%,则增加主元个数
D = flipud(diag(lamda));
num_pc = 1;
while sum(D(1:num_pc))/sum(D) < 0.9
num_pc = num_pc +1;
end
P = T(:,train_col-num_pc+1:train_col); %取与 lamda 相对应的特征向量
%每一列代表一个特征向量
%求置信度为 99%、95%时的 T2 统计控制限
T2UCL1=num_pc*(train_row-1)*(train_row+1)*finv(0.99,num_pc,train_row - num_pc)/(train_row*(train_row - num_pc));
T2UCL2=num_pc*(train_row-1)*(train_row+1)*finv(0.95,num_pc,train_row - num_pc)/(train_row*(train_row - num_pc));
%开始计算SPE统计量
theta = zeros(3,1);
for i = 1:3
theta(i) = sum((D(num_pc+1:train_col)).^i);
end
h0 = 1 - 2*theta(1)*theta(3)/(3*theta(2)^2);
ca = norminv(0.99,0,1);
SPE = theta(1)*(h0*ca*sqrt(2*theta(2))/theta(1) + 1 + theta(2)*h0*(h0 - 1)/theta(1)^2)^(1/h0);
frecord = fopen('./records.txt','w');
for k = 1:21
%第k组测试数据
fprintf(frecord,'故障模式(%d)—',k);
test = cell2mat(testdata(k+1));
%开始在线检测
n = size(test,1);
test=(test-repmat(train_mean,n,1))./repmat(train_std,n,1);
%测试样本归一化
[r,y] = size(P*P');
I = eye(r,y); %单位矩阵
T2_test = zeros(n,1);
SPE_test = zeros(n,1);
T2_falm = 0; SPE_falm = 0;
xf_T2 = []; cf_SPE = [];
for i = 1:n
T2_test(i)=test(i,:)*P/lamda(train_col-num_pc+1:train_col,train_col-num_pc+1:train_col)*P'*test(i,:)';
SPE_test(i) = test(i,:)*(I - P*P')*test(i,:)';
if T2_test(i) > T2UCL1
if i < 161
T2_falm = T2_falm + 1;
else
xf_T2 = cat(1, xf_T2, i);
end
end
if SPE_test(i) > SPE
if i < 161
SPE_falm = SPE_falm + 1;
else
cf_SPE = cat(1, cf_SPE, i);
end
end
end
fprintf(frecord,'T2,SPE(误报数/误报率/漏报率/延迟诊断时间):%3d/%.2f/%.2f/%d, %3d/%.2f/%.2f/%d\n',T2_falm,T2_falm/1.6,100-length(xf_T2)/8,xf_T2(1)-161, SPE_falm,SPE_falm/1.6,100-length(cf_SPE)/8,cf_SPE(1)-161);
%绘图
figure;
% suptitle(['故障模式',num2str(k-1)]);
subplot(221);
plot(1:n,T2_test,'k');
title('主元分析统计量变化图T2');
xlabel('采样数');
ylabel('T^2');
hold on;
line([0,n],[T2UCL1,T2UCL1],'LineStyle','--','Color','r');%画出标志线
line([0,n],[T2UCL2,T2UCL2],'LineStyle','--','Color','g');
subplot(223);
plot(1:n,SPE_test,'k');
title('主元分析统计量变化图SPE');
xlabel('采样数');
ylabel('SPE');
hold on;
line([0,n],[SPE,SPE],'LineStyle','--','Color','r');
%贡献图
%1.确定造成失控状态的得分
pchs = randsample(cf_SPE,1);
fprintf(frecord,'用于计算贡献率的故障点:%d\n',pchs);
S = test(pchs,:)*P(:,1:num_pc);
r = [ ];
for i = 1:num_pc
if S(i)^2/lamda(i) > T2UCL1/num_pc
r = cat(2,r,i);
end
end
%2.计算每个变量相对于上述失控得分的贡献
cont = zeros(length(r),52);
for i = 1:length(r)
for j = 1:52
tmp = abs(S(r(i))/D(r(i))*P(j,r(i))*test(pchs,j));
if tmp < 0
tmp = 0;
end
cont(i,j) = tmp;
end
end
%3.计算每个变量的总贡献
CONTJ = zeros(52,1);
for j = 1:52
CONTJ(j) = sum(cont(:,j));
end
%4.计算每个变量对Q的贡献
e = test(pchs,:)*(I - P*P');
contq = e.^2;
%5. 绘制贡献图
% figure;
subplot(222);
bar(CONTJ*100,'k');
title('T^2贡献率');
xlabel('变量号');
ylabel('%');
subplot(224);
bar(contq*100,'k');
title('Q贡献率');
xlabel('变量号');
ylabel('%');
end
fclose(frecord);
参考
-
JJ. Downs,E.F. Vogel, A plant-wide industrial process control problem[J]. Computers & Chemical Engineering, 1993. 17(3): p. 245-255.
-
P.R. Lyman,C. Georgakis, Plant-wide control of the Tennessee Eastman problem[J]. Computers & Chemical Engineering, 1995. 19(3): p. 321-331.
-
B.M. Wise,N.B. Gallagher, The process chemometrics approach to process monitoring and fault detection[J]. Journal Of Process Control, 1996. 6(6): p. 329 348.
-
C.F. Alcala, S.J. Qin, Reconstruction-based contribution for process monitoring[J]. Automatica, 2009. 45(7): p. 1593-1600.
-
Ian T. Jolliffe. Principal component analysis : A beginner’ s guide[J]. Weather, 1993. 48(8): p. 246–253.
-
Ian. T. Jollife, J. Cadima. Principal component analysis: A review and recent developments[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2016. 374(2065).
-
刘康玲. 基于自适应PCA和时序逻辑的动态系统故障诊断研究[D].浙江大学,2017.


 本文以 Tennessee-Eastman 过程作为系统的实验数据,实验采用主成分分析方法做数据降维,通过监控统计量 T2 和 SPE 来进行故障检测,进一步确定故障变量,最后通过贡献图实现故障隔离。
本文以 Tennessee-Eastman 过程作为系统的实验数据,实验采用主成分分析方法做数据降维,通过监控统计量 T2 和 SPE 来进行故障检测,进一步确定故障变量,最后通过贡献图实现故障隔离。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号