【原子物理】1. 电子排布、量子数与光谱项
~
故事是这样的,2022年秋冬学期某华东地区大学物理学院的《原子物理》课程,非常有幸地请到我的两位室友作为助教
再然后呢,我也有幸()地被两位室友请去友情讲(shui)了半节课,现在我打算来记录一下这次讲课的内容
(2022年11月9日更新,施工结束啦~)
1 从高中化学开始
关于原子结构的故事需要从高中化学选修三讲起。这本书我高中的时候是没有学过的,直到前几年才自学了一遍,这才对原子结构有了更为图像化的认知——
1.1 能层与能级
首先,在多电子的原子核外电子的能力是不同的,按电子的能力差异,可将核外电子分成不同的能层,用 K、L、M、N、O...来标志(即从 K 开始的连续的英文字母)。
能层能够表示两方面意义:(1)电子到原子核的平均距离不同,(2)电子的能力不同。
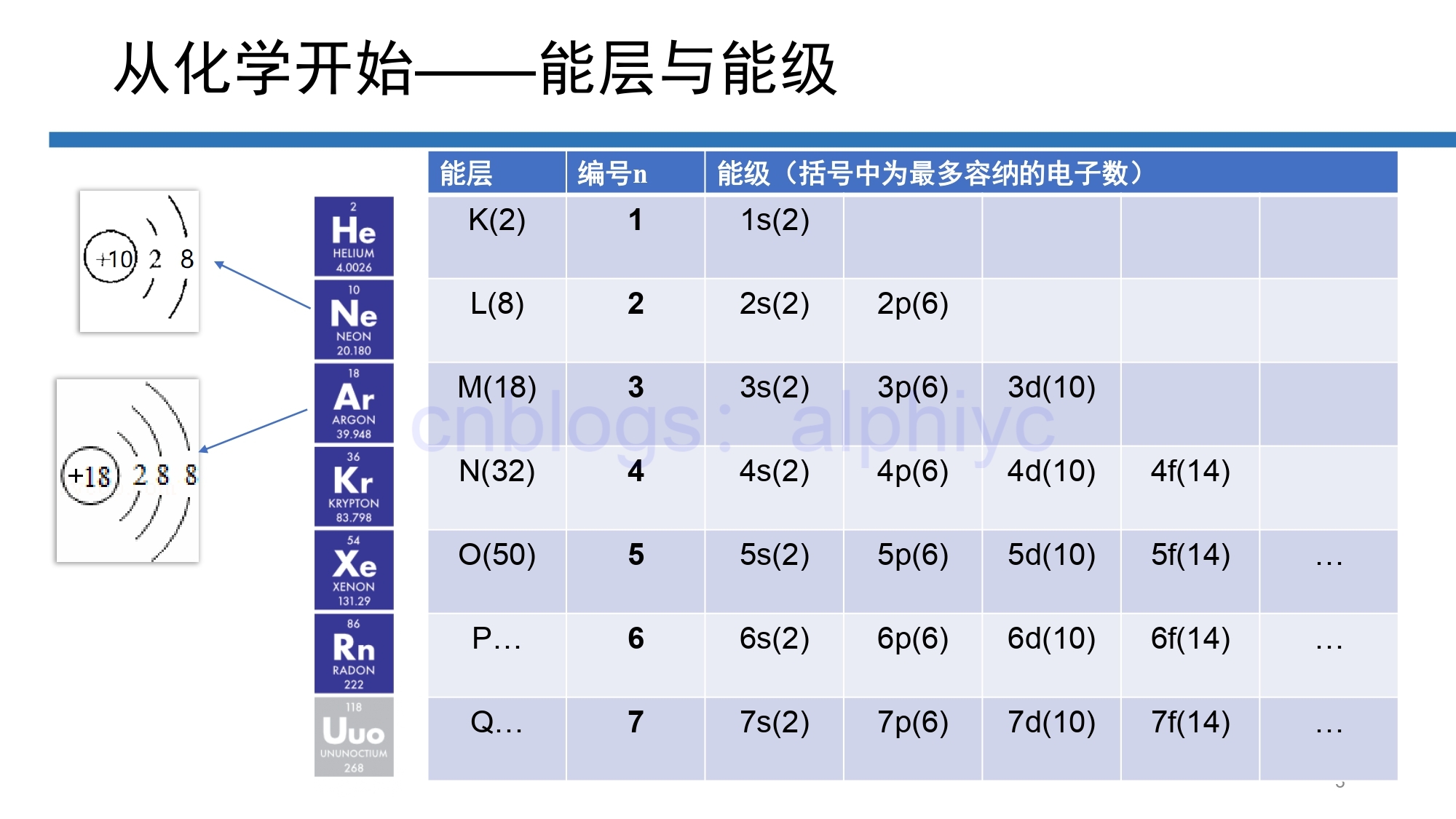
另外的,高中化学还告诉我们,在多电子原子中,同一能层的电子能量也不同,还可以把它们分成能级,用能级的 “编号”值 n 后加 s、p、d、f、g... 来标志(前四个分别为“锐利”的sharp、“模糊”的diffuse、“最强最亮”的principal、“与波尔模型一致”的fundamental,再之后的能级就都是按照字母顺序表(排除j)来命名的)。[1]
1.2 电子排布式
电子排布式,是用能级符号及能级中电子的数目表达核外电子运动状态的一种表达式,其具体写法规则为:分别用1、2、3、4、5、6、7等数字表示K、L、M、N、O、P、Q等电子层,用s、p、d、f、g等符号分别表示各电子亚层,并在这些符号右上角用数字表示各亚层上电子的数目。

另外地,电子排布式中的内层电子排布可用相应的稀有气体的元素符号加方括号来表示,其中,以稀有气体的元素符号加方括号的部分称为“原子实”。这样写,一是可以简化电子排布式,二是可以突出原子的价电子排布。例如,钾的电子排布式是 \(1s^22s^22p^63s^23p^64s^1\) ,其价电子是 4s 能级的那一个电子,最终简化的电子排布式就是 \([Ar]4s^1\) 。
1.3 电子云与轨道
某个能级上的电子,并没有确定的动量和位置,而是弥散成一个电子云。
明晰了电子云的概念,就可以给出能级这个概念的一部分含义——能级能够表示两方面意义:(1)表示电子云形状不同,s电子云是以原子核为中心的球形,p电子云是表示以原子核为中心的无柄哑铃型(纺锤形),d和f电子云形状更复杂;(2)表示能量不同,对多电子原子,一般而言,s、p、d、f 等能级的电子能量依次增高。[2]
注意到,ns能级的电子云,它是一个球,球具有球对称性,因此只有一种,即ns能级上只有一个轨道。又注意到,np能级的电子云是纺锤状的,其中含有3个原子轨道,相互垂直(分别用px、py、pz表示)。

另外地,由于电子自旋的存在,一个轨道里可以容纳两个电子,因此,若以 l = 0、1、2... 来表示 s、p、d... ,nl 能级可以容纳的轨道数目就是 4l+2,与前几面ppt直接给出的结果是相符的。(好耶✌️高中化学就复习到这儿了)
2 如何量子力学地描述一个电子的“位置”
我们赶紧来回忆一下,上面的分析中,从一个完整的原子,到某个“具体”的电子,经历了能层(用n编号)、能级(用l编号)、轨道(现在我们用m编号,如图所示)、轨道里的两个电子(用 m_s 编号,如图所示)四个“阶段”。

用四个数字来表示这四个阶段,也即 \(n\,l\,m\,m_s\) ,它们分别为 主量子数、角量子数、磁量子数、电子自旋磁量子数 ,它们的取值范围都在PPT里标明了,其值都为整数或者半整数(1/2或者-7/2这样的)
下面,我们要借由量子力学的手段,来告诉大家,为什么一定要写出这四个量子数来。
2.1 氢原子中电子的“位置”
在量子力学中,为了描述某个粒子,需要用薛定谔方程解出波函数来。在写出波函数后,粒子的一切性质就都清楚了。

PPT中,我们完成了对氢原子波函数的求解,其解的情况是这样的——氢原子波函数分为两部分:一是径向的 \(R_nl(r)\) ,是一个拉盖尔-勒朗德函数,由 n 与 l 两个量子数决定;二是角向的 \(Y_{l,m}(\theta,\phi)\) ,是一个球谐函数,由 l 与 m 两个量子数决定。(事实上另外还需要电子自旋角量子数 \(s\) 与电子自旋磁量子数 \(m_s\) ,但这两个量子数所确定的是电子自旋的内禀空间里面的事情,就先不管它了)
这两个特殊函数的图示都展示在了PPT中,相当于在图像上就完全了解了氢原子的波函数,我们来分析一下:
- 不同的 n, l, m 值,决定了一个确定的波函数,也就是一个确定的态,因此它们这几个量子数,是可以完整地确定下一个电子的“位置”的(其实说电子处于哪一个态会更严格一些,不过作为搞实验的我就不管那么多了🐶);
- “l=0, m=0” 那一个其实就是 s 能级(无论是哪个能层的),同样地 “l=1, m=-1、0、1” 那一排其实就是 p 能级(无论是哪个能层的),3个不同的 m 值分别对应 px、py 与 pz ;
- n 的取值对 l 的取值有限制作用,而 l 的取值对 m 的取值有限制作用,这些限制都是由于特殊函数本身的性质带来的,也就是说,原子物理里面这些量子数的取值范围是有其数学来源的;
- 对于这样一个确定的“态”而言,其能量值也是确定的,我们把它写出来——

这里我们计算出了氢原子中电子不同态的能量,我们惊奇地发现,这个能量值仅仅与 n 有关,这一现象称为“偶然简并”,是氢原子这种情况所独有的。在多电子情况下,偶然简并不复存在,角量子数 l 也会对能量值产生影响——也就是说,如果某个多电子原子的价电子在同一个能层的不同能级之间跃迁,其能量也会有不同。下面我们借着铷原子的例子来实际分析一下——
2.2 铷原子中电子的“位置”
铷(Rubidium),元素符号为Rb,原子序数为37,是一种碱金属元素,单质是银白色轻金属,质软而呈蜡状,其化学性质比钾活泼。在光的作用下易放出电子。[3]
多电子原子的复杂,首先就在于其哈密顿量的复杂性——不仅有原子核和电子之间的相互作用,还有电子与电子之间的,另外即便是氢原子本身,也要考虑到电子自旋与电子轨道角动量之间、电子总角动量之间的相互作用等等等等。将这些作用全部考虑进去后,我们就需要替换或加入一些新的量子数,才能完整地描述电子所处的态——这些好量子数都写在PPT里了:

在引入了这些新的量子数后,新的量子数也大都会对能量值产生影响。也就是说,原本 n、l 相同,能量值就相同,但由于这些新考虑进来的修正项, n、l 相同的量子态能量就有可能不再相同了——这就是原子的精细能级劈裂,乃至超精细能级劈裂。一般说来,从原子内态的描述来看,到了PPT里这一堆好量子数所描述的超精细结构,描述原子能级的自由度就完备了。
当然PPT里还标出了这些量子数的取值范围,有心的读者可以待会儿对照着我们即将看到的实例,来验证一下这些取值范围有没有被违反😉
3 铷原子光谱及其塞曼效应
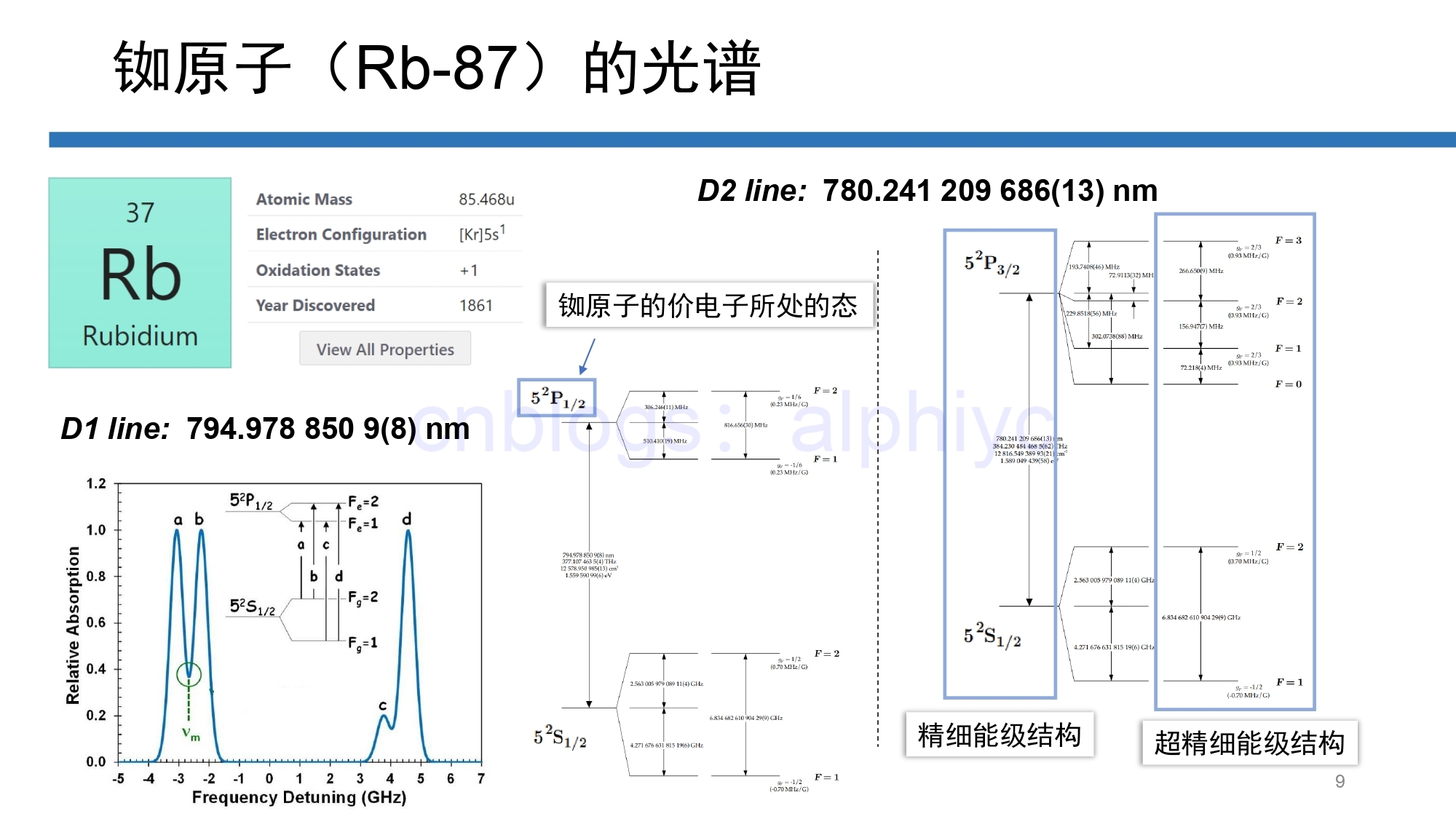
如图所示,铷原子的的光谱,大概是这样一个情况:
你如果拿一个有角色散功能的器件(比如光栅)去看它的发射光谱,可以粗略地看到两条谱线:D1线(795nm,377THz 注:1THz = 10^12 Hz)与 D2线(780nm,384THz)。
这两条谱线的成因是这样的:铷原子的那个价电子,其基态位于 \(5^2S_{1/2}\) ,分别可以跃迁到两个激发态 \(5^2P_{1/2}\) (能量较低,对应 D1线)与 \(5^2P_{3/2}\) (能量较高,对应 D2线),因此产生了这样的两条谱线。
当然了,上面看到的所谓 “\(5^2P_{3/2}\)” 之类的符号究竟是什么东西呢,下面我们来介绍一下这种原子光谱项符号的具体含义——
如图所述,5 代表 主量子数 n,大写的 P 代表角量子数 L = 1(多电子原子一般改用大写字母),P 左上的 2 是 2S+1 = 2(2S+1 叫光谱的多重性,可以说它对应着一个轨道里能塞下几个电子,或者对应着总角动量 J 可以取多少个不同的数值),P 右下的 3/2 是电子总角动量 J ,J 的两个取值就对应了两条 D 线。
这两个激发态的不同,属于精细结构。现在,我们再计入铷原子核核自旋 I = 5/2 的作用,由于各个态原子总角动量 F 的不同,就劈裂出了超精细结构(看PPT里的最右边),运用这些超精细能级,可以完成许多非常神奇的原子物理与光学实验。

我们回溯到氢原子能量的计算那里,在那里我们发现,氢原子的能量值与磁量子数 \(m\) 也是没有关系的,其数学上的来源是势场的球对称性。现在,我们在空间中加上磁场,具有不同的原子总角动量磁量子数 \(m_F\) 的态,其能量也不再相同,并且随着磁场大小的变化,其能级位置也会移动,这个现象,就称为塞曼效应,下面的能级移动图里,就形象化地展示了这种现象:

最后,不知道有心的读者有没有一直在验证这些量子数取值范围的合理性,那么最后塞曼效应这里也正式地计算了一下态的数目,可以借此对照一下自己的答案哦(绝对不是懒得码字了而是希望留做习题😏🐶)
之后可能还会写一些相关的AMO入门级内容,希望自己不会断更😎,这篇随笔就到此结束啦,希望有人能喜欢~


 浙公网安备 33010602011771号
浙公网安备 33010602011771号