【NOIP2015提高组】 Day1 T2 信息传递
题目描述
有n个同学(编号为1到n)正在玩一个信息传递的游戏。在游戏里每人都有一个固定的信息传递对象,其中,编号为i的同学的信息传递对象是编号为Ti同学。
游戏开始时,每人都只知道自己的生日。之后每一轮中,所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象(注意:可能有人可以从若干人那里获取信息,但是每人只会把信息告诉一个人,即自己的信息传递对象)。当有人从别人口中得知自己的生日时,游戏结束。请问该游戏一共可以进行几轮?
输入输出格式
输入格式:
输入共2行。
第1行包含1个正整数n表示n个人。
第2行包含n个用空格隔开的正整数T1,T2,……,Tn其中第i个整数Ti示编号为i
的同学的信息传递对象是编号为Ti的同学,Ti≤n且Ti≠i
数据保证游戏一定会结束。
输出格式:
输出共 1 行,包含 1 个整数,表示游戏一共可以进行多少轮。
输入输出样例
输入样例#1:
5 2 4 2 3 1
输出样例#1:
3
说明
样例1解释
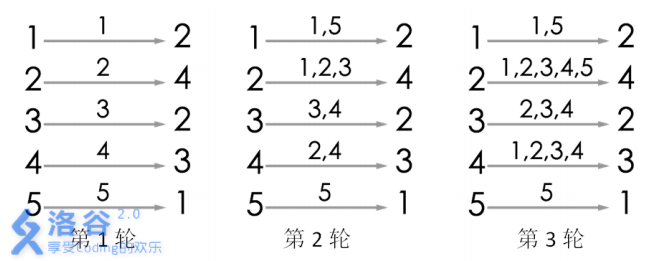
游戏的流程如图所示。当进行完第 3 轮游戏后, 4 号玩家会听到 2 号玩家告诉他自
己的生日,所以答案为 3。当然,第 3 轮游戏后, 2 号玩家、 3 号玩家都能从自己的消息
来源得知自己的生日,同样符合游戏结束的条件。
对于 30%的数据, n ≤ 200;
对于 60%的数据, n ≤ 2500;
对于 100%的数据, n ≤ 200000。
题解:
不难看出,题目要求的是该图中包含点数最少但点数≥2的环所包含的点数。
直接对于每个点进行dfs求最小的环即可
但这种做法是O(n^2)的,考虑到n≤500,000,故需进行优化
考虑到题目中所求环为最小,那么当搜索到一个点在上一轮已经被遍历过时,其必找到另一个环,则不用向该点继续搜索。故每个点有且只有被遍历一次,时间复杂度为O(n)
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<stack> 5 #define M 210000 6 #define INF 123123123 7 using namespace std; 8 int nx[M]={0},n,vis[M]={0},t=0; 9 bool b[M]={0}; 10 stack<int> s; 11 int bfs(int x){ 12 vis[x]=++t; 13 if(nx[x]==x) return INF; 14 b[x]=1; s.push(x); 15 while(!vis[nx[x]]){ 16 x=nx[x]; 17 vis[x]=++t; 18 b[x]=1; s.push(x); 19 } 20 if(b[nx[x]]){ 21 while(!s.empty()) b[s.top()]=0,s.pop(); 22 return vis[x]-vis[nx[x]]+1; 23 }else{ 24 while(!s.empty()) b[s.top()]=0,s.pop(); 25 return INF; 26 } 27 } 28 29 int main(){ 30 freopen("message.in","r",stdin); 31 freopen("message.out","w",stdout); 32 scanf("%d",&n); int minn=INF; 33 for(int i=1;i<=n;i++) scanf("%d",nx+i); 34 for(int i=1;i<=n;i++) if(!vis[i]) 35 minn=min(minn,bfs(i)); 36 cout<<minn<<endl; 37 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号