利用c++编写bp神经网络实现手写数字识别详解
利用c++编写bp神经网络实现手写数字识别
写在前面
从大一入学开始,本菜菜就一直想学习一下神经网络算法,但由于时间和资源所限,一直未展开比较透彻的学习。大二下人工智能课的修习,给了我一个学习的契机。现将bp神经网络的推导和实践记录于此:
前置知识
微积分相关内容,如偏导,梯度等
(大一不懂偏导梯度,这就是我学不进去的原因)
BP神经网络概况及计算方法
可以理解为一个多层的网络,包含输入层X,隐藏层H和输出层Y,其中隐藏层可以不止一层。
为了直观展示,隐藏层和输出层都被我拆成了两层进行讲解
以下为网络中每个元素的定义,及正向传播过程
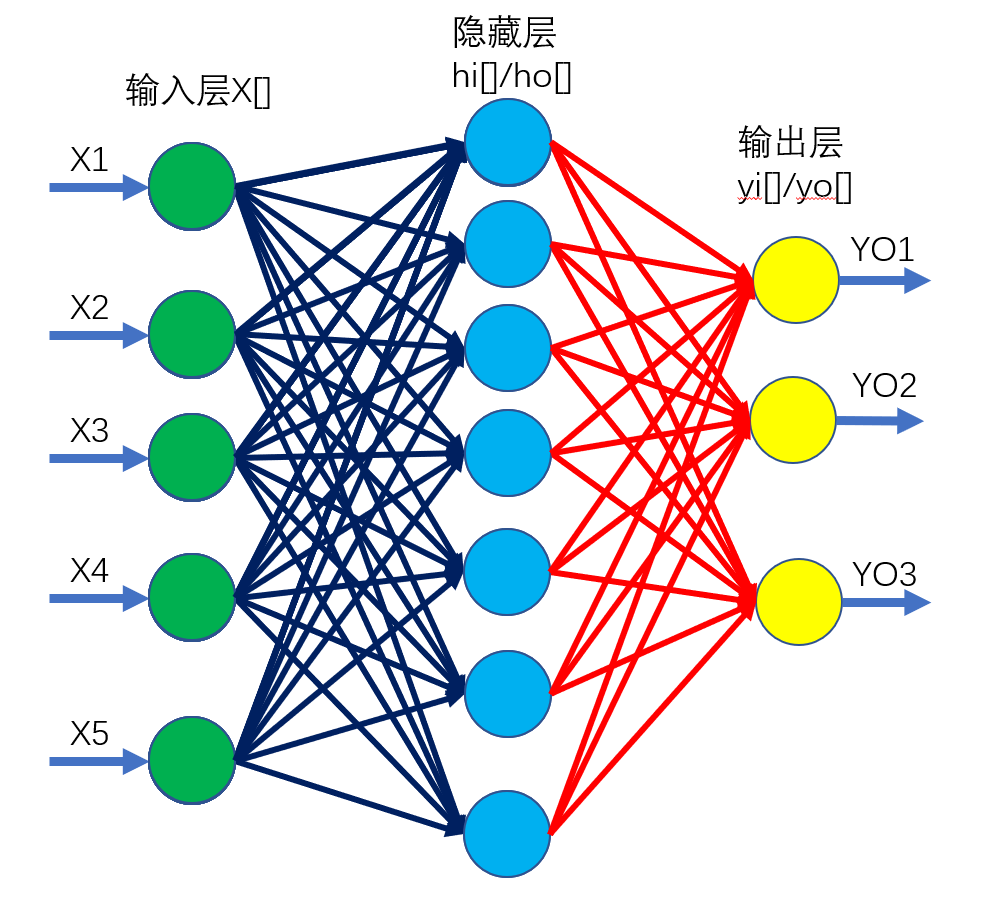
\(x[1],x[2],……x[n]\)共n个点,表示输入层,所有的数据都是从该层输入。
在本手写数字识别模型中,输入的是\(28\times 28\)的灰度图,故输入层包含784个节点,值域为\([0,1]\)
第一组连边w1,为输入层X和隐藏层H之间的全连接,共\(n\times p\)条边
其中\(w1[i][j]\)表示从输入层第i个节点,连向隐藏层第j个节点的边的边权
第二组连边w2,为隐藏层H和输出层y之间的全连边,共\(p\times q\)条边
神经网络的学习过程,即在外界输入样本的刺激下不断改变网络的连接权值,以使网络的输出不断地接近期望的输出。
在拥有足够多隐藏层神经元的情况下,两层神经网络可以拟合任意连续函数,三层神经网络可以拟合任意函数。
如果这个网络上有m个隐藏层,则总共会有m+1组连边,本代码中m=1
连边的权值是整个网络的关键所在,当连边边权确定后,即可得到一个网络
为了直观展示,隐藏层H被我拆为了两个部分进行讲解
\(hi[1],hi[2],……hi[p]\)共p个点,表示计算后的隐藏层
其中\(hi[k]=\sum\limits_{l=1}^{n}x[l]\times w1[l][k]\)
我们也可以用矩阵乘法来表示,\(hi=x\times w1\)
\(ho[1],ho[2],……ho[p]\)共p个点,其中\(ho[i]=f(hi[i])\),\(f(x)\)表示一个激活函数
本代码中,激活函数采用\(sigmoid\)函数
求解输出层y的过程和h的过程类似
有\(yi[k]=\sum\limits_{l=1}^{p}ho[l]\times w2[l][k]\)
有\(yo[k]=f(yi[k]),f(x)\)表示一个激活函数,本代码中y的激活函数同样采用\(sigmoid\)
在最终的输出中\(yo[k]\)的含义是:输入图片所表示的数字是k的概率为多少
正向计算代码如下:
//前向传播函数
void forward(){
//计算hi前需要对其进行清空
memset(hi,0,sizeof(hi));
//通过w1计算输入层-隐藏层输入节点
for(int i=0;i<n;i++)
for(int j=0;j<p;j++)
hi[j]+=x[i]*w1[i][j];
//通过激活函数对隐藏层进行计算
for(int i=0;i<p;i++)
ho[i]=sigmoid(hi[i]);
//计算yi前需要对其进行清空
memset(yi,0,sizeof(yi));
//通过w2计算隐藏层-输出层
for(int i=0;i<p;i++)
for(int j=0;j<q;j++)
yi[j]+=ho[i]*w2[i][j];
//通过激活函数求yo
for(int i=0;i<q;i++)
yo[i]=sigmoid(yi[i]);
}
Sigmoid函数
\(Sigmoid\)函数将被用于本菜菜编写的神经网络中,其表达式如下:
它可以将一个实数映射到(0,1)的区间上,在特征相差不是特别大时效果较好,其函数图形如下:
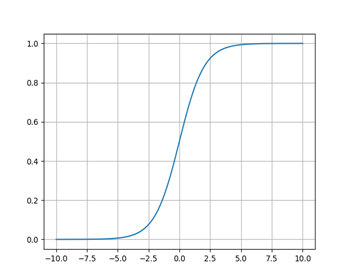
在本人实现的\(bp\)神经网络中,隐藏层的\(h\)和输出层的\(y\)都会由\(sigmoid\)函数进行处理
sigmoid函数求导
在后续求梯度的过程中,需要对sigmoid函数求导
sigmoid函数有一神器性质,即\(sigmoid'(x)=sigmoid(x)\times(1-sigmoid(x))\),推导过程如下:
该公式可降低求梯度公式的计算量
我们用\(dsigmoid(y)=sigmoid'(x)\),其中\(y=sigmoid(x)\)
sigmoid和dsigmoid代码
//激活函数
double sigmoid(double x){
return 1/(1+exp(-x));
}
//已知x=sigmoid(y),返回sigmoid'(y)
double dsigmoid(double x){
return x*(1-x);
}
反向传播
现在我们已经通过正向传播,求解出了对应的输出,但这个输出可能和我们的期望有所不同(如将8识别为了6)。我们要对其误差进行修正。
我们定义误差函数\(e=\frac{1}{2}\sum\limits_{k=0}^{9}(yo[k]-d[k])^2\)
其中序列\(d\)表示第\(k\)个输出节点的正确值,在本案例中,假设正确数字为\(num\),则有\(d[num]=1\),其余的\(d\)均为\(0\)
修正误差,显然就是降低e的值,而在模型中,输入是固定的,在不改动模型的情况下,提高正确率可通过修改w1和w2的权值实现。
因此,我们需要求\(\dfrac{\partial e}{\partial w1} 和 \dfrac{\partial e}{\partial w2}\),然后借此对边权进行修正
修正w1
边权是一条一条进行修正的,假设我们要修正\(w2[i][j]\),由链式法则,修正公式如下:
我们对每个模块分别求偏导,考虑\(\dfrac{\partial e}{\partial yo[j]}\),有:
在第1个等式到第2个等式,以及第3个等式到第4个等式的时候,都是将常数项进行了舍弃
考虑\(\dfrac{\partial yo[j]}{\partial yi[j]}\),我们发现这个就是求\(sigmoid'(yi[j])\),根据上文中的式子,我们可以得到:
$\dfrac{\partial yo[j]}{\partial yi[j]}=sigmoid(yi[j])\times (1-sigmoid(yi[j]))=dsigmoid(yo[j]) $
考虑\(\dfrac{\partial yi[j]}{\partial w2[i][j]}\),我们将\(yi[j]\)的求解公式代入,我们可以得到:
综上,我们得到:
那么问题来了,如何用求出来的这个公式修正w2?
其实直接令\(w2[i][j]-=\eta \times \dfrac{\partial e}{\partial w2[i][j]}\)其实就可以进行修正了,其中\(\eta\)表示修正因子,为一个常量,本人设置为0.1
为什么可以呢?一个直观的表达为: 当误差对权值的偏导数大于零时,权值调整量为负,实际输出大于期望输出,权值向减少方向调整,使得实际输出与期望输出的差减少。当误差对权值的偏导数小于零时,权值调整量为正,实际输出小于期望输出,权值向增加方向调整,使得实际输出与期望输出的差减小。
修正w2
和w1类似,由链式法则,得:
为什么这里需要出现\(\sum\),主要是隐藏层节点j,可以向外连接多个输出层节点k,而这多个输出层节点k都对e会产生影响。
然后,上述式子分解步数过多,我们将\(\dfrac{\partial yi[k]}{\partial w2[j][k]} \times \dfrac{\partial w2[j][k]}{\partial ho[j]}\)进行合并,得到:
子项\(\dfrac{\partial e}{\partial yo[k]}\times \dfrac{\partial yo[k]}{\partial yi[k]}\)在求w2的过程中已经求得,即为\((yo[k]-d[k]) \times dsigmoid(yo[k])\)
由于两层激活函数相同,子项\(\dfrac{\partial ho[j]}{\partial hi[j]}\)等价于求w2过程中计算过的\(\dfrac{\partial yo[j]}{\partial yi[j]}\),等于\(dsigmoid(ho[j])\)
由于两层前向传播相同,子项\(\dfrac{\partial hi[j]}{\partial w1[i][j]}\)等价于求w2过程中计算过的\(\dfrac{\partial yi[j]}{\partial w2[i][j]}\),等于\(x[i]\)
考虑\(\dfrac{\partial yi[k]}{\partial ho[j]}\),我们得到:
综上,我们得到:
更新方式和w2相同
反向传播代码
严格按照上述式子编写的更新代码如下:
void back_old(){
//对w2进行更新
for(int i=0;i<p;i++)
for(int j=0;j<q;j++){
double delta=(yo[j]-d[j])*dsigmoid(yo[j])*ho[i];
w2[i][j]-=delta*learnRate;
}
//对w1进行更新
for(int i=0;i<n;i++)
for(int j=0;j<p;j++){
double delta=0;
for(int k=0;k<q;k++)
delta+=(yo[k]-d[k])*dsigmoid(yo[k])*dsigmoid(ho[j])*x[i]*w2[j][k];
w1[i][j]-=delta*learnRate;
}
}
该代码的时间复杂度为\(O(npq)\),考虑对求w1偏导的代码进行优化
对求w1偏导的和式进行移项,我们得到:
我们开一个预处理序列W2,其中
在处理出W2后,求偏导的式子可以化简为:
则可以将时间复杂度降低到\(O(np+pq)\)
代码如下:
void back(){
//对w2进行更新
for(int i=0;i<p;i++)
for(int j=0;j<q;j++){
double delta=(yo[j]-d[j])*dsigmoid(yo[j])*ho[i];
w2[i][j]-=delta*learnRate;
}
//对反向传播进行预处理
double W2[p];
memset(W2,0,sizeof(W2));
for(int j=0;j<p;j++)
for(int k=0;k<q;k++)
W2[j]+=(yo[k]-d[k])*dsigmoid(yo[k])*w2[j][k];
//对w1进行更新
for(int i=0;i<n;i++)
for(int j=0;j<p;j++){
double delta=dsigmoid(ho[j])*x[i]*W2[j];
w1[i][j]-=delta*learnRate;
}
}
Minst数据集
本bp代码所使用的数据来自该数据集
该部分将介绍所使用的的训练集数据格式,可以直接看我的代码来了解读入规则
MNIST是一个手写体数字的图片数据集,该数据集来由美国国家标准与技术研究所(National Institute of Standards and Technology (NIST))发起整理,一共统计了来自250个不同的人手写数字图片,其中50%是高中生,50%来自人口普查局的工作人员。该数据集的收集目的是希望通过算法,实现对手写数字的识别。
数据下载
官网上提供了数据集的下载链接
| 文件下载 | 文件用途 |
|---|---|
| train-images-idx3-ubyte.gz | 训练集图像 |
| train-labels-idx1-ubyte.gz | 训练集标签 |
| t10k-images-idx3-ubyte.gz | 测试集图像 |
| t10k-labels-idx1-ubyte.gz | 测试集标签 |
在上述文件中,训练集一共包含了 60,000 张图像和标签,而测试集一共包含了 10,000 张图像和标签。测试集中前5000个来自最初NIST项目的训练集.,后5000个来自最初NIST项目的测试集。前5000个比后5000个要规整,这是因为前5000个数据来自于美国人口普查局的员工,而后5000个来自于大学生。
数据集解读
下载上述四个文件后,将其解压会发现,得到的并不是一系列图片,而是 .idx1-ubyte和.idx3-ubyte 格式的文件。这是一种IDX数据格式,其基本格式如下:
magic number
size in dimension 0
size in dimension 1
size in dimension 2
.....
size in dimension N
data
其中magic number为4字节,前2字节永远是0,第3字节代表数据的格式:
0x08: unsigned byte
0x09: signed byte
0x0B: short (2 bytes)
0x0C: int (4 bytes)
0x0D: float (4 bytes)
0x0E: double (8 bytes)
第4字节的含义表示维度的数量(dimensions): 1 表示一维(比如vectors), 2 表示二维( 比如matrices),3表示三维(比如numpy表示的图像,高,宽,通道数)。
训练集和测试集的标签文件的格式(train-labels-idx1-ubyte和t10k-labels-idx1-ubyte)
idx1-ubtype的文件数据格式如下:
[offset] [type] [value] [description]
0000 32 bit integer 0x00000801(2049) magic number (MSB first)
0004 32 bit integer 60000 number of items
0008 unsigned byte ?? label
0009 unsigned byte ?? label
........
xxxx unsigned byte ?? label
第0 ~ 3字节,是32位整型数据,取值为0x00000801(2049),即用幻数2049记录文件数据格式,这里的格式为文本格式。
第4~7个字节,是32位整型数据,取值为60000(训练集时)或10000(测试集时),用来记录标签数据的个数;
第8个字节 ~ ),是一个无符号型的数,取值为对应0~9 之间的标签数字,用来记录样本的标签。
训练集和测试集的图像文件的格式(train-images-idx3-ubyte和t10k-images-idx3-ubyte)
idx3-ubtype的文件数据格式如下:
[offset] [type] [value] [description]
0000 32 bit integer 0x00000803(2051) magic number
0004 32 bit integer 60000 number of images
0008 32 bit integer 28 number of rows
0012 32 bit integer 28 number of columns
0016 unsigned byte ?? pixel
0017 unsigned byte ?? pixel
........
xxxx unsigned byte ?? pixel
即:
第0 ~ 3字节,是32位整型数据,取值为0x00000803(2051),即用幻数2051记录文件数据格式,这里的格式为图片格式。
第4~7个字节,是32位整型数据,取值为60000(训练集时)或10000(测试集时),用来记录图片数据的个数;
第8~11个字节,是32位整型数据,取值为28,用来记录图片数据的高度;
第12~15个字节,是32位整型数据,取值为28,用来记录图片数据的宽度;
第16个字节 ~ ),是一个无符号型的数,取值为0~255之间的灰度值,用来记录图片按行展开后得到的灰度值数据,其中0表示背景(白色),255表示前景(黑色)。
代码
#include<bits/stdc++.h>
using namespace std;
//激活函数
double sigmoid(double x){
return 1/(1+exp(-x));
}
//已知x=sigmoid(y),返回sigmoid'(y)
double dsigmoid(double x){
return x*(1-x);
}
#define learnRate 0.2 //学习率
#define n 784 //输入层点个数
#define p 500 //隐藏层节点个数
#define q 10 //输出层节点个数
//与推导公式保持一致
double x[n],hi[p],ho[p],yi[q],yo[q],d[q];
//所训练的网络,采用两个矩阵表示
double w1[n][p],w2[p][q];
//随机生成一个-1到1的数
double ranDouble(){
return rand()%10/5.-1;
}
void init(){
for(int i=0;i<n;i++)
for(int j=0;j<p;j++)
w1[i][j]=ranDouble();
for(int i=0;i<p;i++)
for(int j=0;j<q;j++)
w2[i][j]=ranDouble();
}
//前向传播函数
void forward(){
//计算hi前需要对其进行清空
memset(hi,0,sizeof(hi));
//通过w1计算输入层-隐藏层输入节点
for(int i=0;i<n;i++)
for(int j=0;j<p;j++)
hi[j]+=x[i]*w1[i][j];
//通过激活函数对隐藏层进行计算
for(int i=0;i<p;i++)
ho[i]=sigmoid(hi[i]);
//计算yi前需要对其进行清空
memset(yi,0,sizeof(yi));
//通过w2计算隐藏层-输出层
for(int i=0;i<p;i++)
for(int j=0;j<q;j++)
yi[j]+=ho[i]*w2[i][j];
//通过激活函数求yo
for(int i=0;i<q;i++)
yo[i]=sigmoid(yi[i]);
}
//判断输出的答案是多少
int getAns(){
int ans=0;
for(int i=1;i<q;i++)
if(yo[i]>yo[ans]) ans=i;
return ans;
}
//反向传播函数
void back_old(){
//对w2进行更新
for(int i=0;i<p;i++)
for(int j=0;j<q;j++){
double delta=(yo[j]-d[j])*dsigmoid(yo[j])*ho[i];
w2[i][j]-=delta*learnRate;
}
//对w1进行更新
for(int i=0;i<n;i++)
for(int j=0;j<p;j++){
double delta=0;
for(int k=0;k<q;k++)
delta+=(yo[k]-d[k])*dsigmoid(yo[k])*dsigmoid(ho[j])*x[i]*w2[j][k];
w1[i][j]-=delta*learnRate;
}
}
//反向传播函数
void back(){
//对w2进行更新
for(int i=0;i<p;i++)
for(int j=0;j<q;j++){
double delta=(yo[j]-d[j])*dsigmoid(yo[j])*ho[i];
w2[i][j]-=delta*learnRate;
}
//对反向传播进行预处理
double W2[p];
memset(W2,0,sizeof(W2));
for(int j=0;j<p;j++)
for(int k=0;k<q;k++)
W2[j]+=(yo[k]-d[k])*dsigmoid(yo[k])*w2[j][k];
//对w1进行更新
for(int i=0;i<n;i++)
for(int j=0;j<p;j++){
double delta=dsigmoid(ho[j])*x[i]*W2[j];
w1[i][j]-=delta*learnRate;
}
}
FILE *fImg,*fAns;
int last[100000];
void train(int cas){
//读入一张新的图片
//除了前16字节,接下来的信息都是一张一张的图片
//每张图片大小为28*28,每个char表示该像素对应的灰度,范围为0至255
unsigned char img[n],num;
fread(img,1,n,fImg);
for(int i=0;i<n;i++) x[i]=img[i]/255.;
//读入该图片对应的答案
//除了前8字节,第k个字节对应第k张图片的正确答案
fread(&num,1,1,fAns);
for(int i=0;i<q;i++) d[i]=(num==i);
forward();
int ans=getAns();
last[cas]=(num==ans);
back();
//输出最近100局的正确率
int P=100,hh=0;
if(cas%P==0){
for(int i=0;i<P;i++)
hh+=last[cas-i];
printf("%d %d\n",cas,hh);
}
}
//int imgs=16,nums=8;
int main(){
fImg=fopen("train-images.idx3-ubyte","rb");
fseek(fImg,16,SEEK_SET);
fAns=fopen("train-labels.idx1-ubyte","rb");
fseek(fAns,8,SEEK_SET);
init();
for(int cas=1;cas<=60000;cas++){
train(cas);
}
}
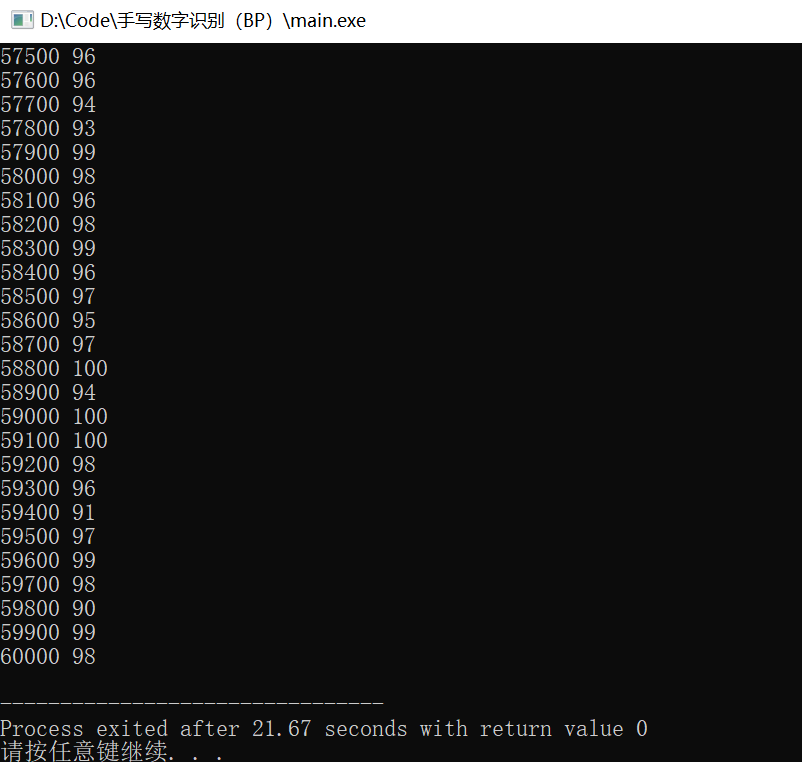
训练效果
在隐藏层点数设置为500时,完成60000次训练,需要21s
最后2500次训练的正确率如图所示,平均约为97%:
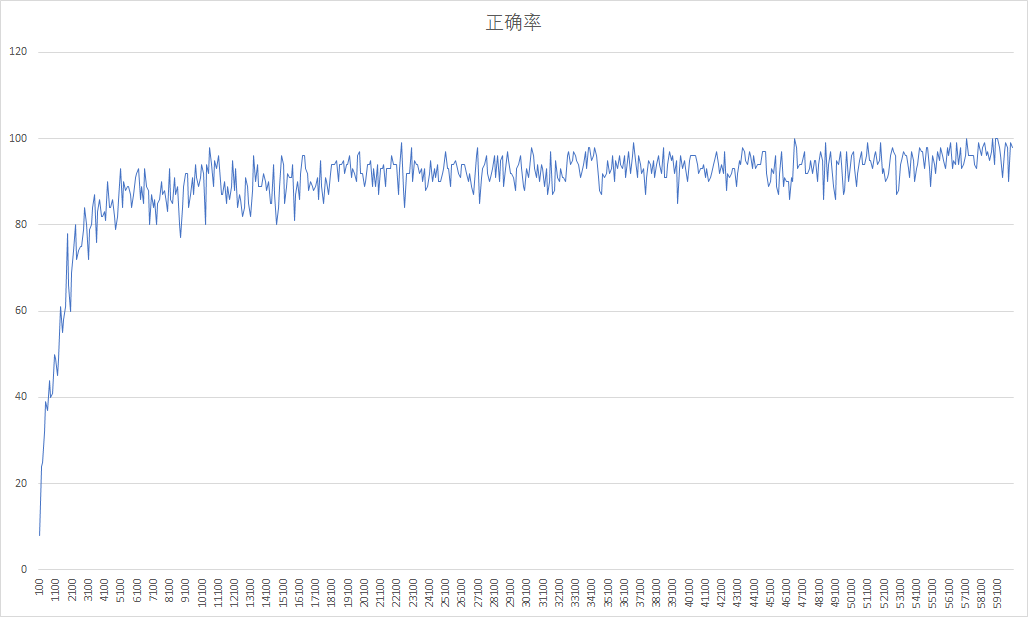
训练次数-正确率曲线如图所示:


 浙公网安备 33010602011771号
浙公网安备 33010602011771号