【NOI2019集训题2】 序列 后缀树+splay+dfs序
题目大意:给你一个长度为$n$的序列$a_i$,还有一个数字$m$,有$q$次询问
每次给出一个$d$和$k$,问你对所有的$a_i$都在模$m$意义下加了$d$后,第$k$小的后缀的起点编号。
数据范围:$n≤100000,d≤a_i<m≤10^9,q≤5\times 10^5$
这一题我想的时候被最后一步卡主了(其实如果到那个时候估计也时间不够了)
我们不难找出一个单次询问$O(n)$的方法,我们每次暴力更新$a_i$,然后对原序列搞一棵后缀树出来,在上面暴力查询第$k$小即可。
如果没有加$d$的操作,只是单纯询问第k大的话,我们考虑对这棵后缀树按字典序先序遍历一遍,搞出dfs序,用平衡树维护这些点出现的先后顺序。
对于一次询问第$k$小,我们在平衡树上找出dfs序第$k$小的后缀节点出来,输出即可。
下面考虑加$d$的操作。
考虑到这一题并没有要求强制在线,我们考虑对所有的询问按$d$从小大到大排序。
随着d的增长,原先最大的数随着取模操作的发生,会变成最小的数。
也就是说会出现一个换位的情况
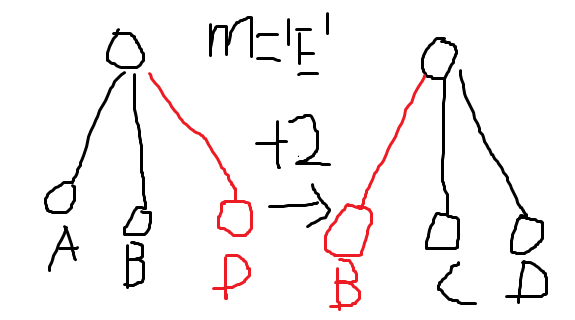
就像这样
显然这个红点下面还会接很多个节点,但是不管怎么换位,以红点为根的子树内孩子的数量是不会变的。
我们只需要不断地做搬动节点的操作(在平衡树中,取出一个区间,并把这个区间插入到另一个区间中),并且动态维护dfs序列即可。
在询问离线后,我们不难发现每个节点至多只需要被搬动一次。
那么时间复杂度就变成愉快的O((n+q)\ log\ n)了。
然而我在想的时候,并没有往dfs序上想,sam也不熟练
注意细节!
1 #include<bits/stdc++.h> 2 #define M 200005 3 #define lc(x) ch[(x)][0] 4 #define rc(x) ch[(x)][1] 5 using namespace std; 6 7 int dfn[M]={0},low[M]={0},t=0; int n,m,q; 8 9 namespace H{ 10 int ch[M][2]={0},fa[M]={0},root,siz[M]={0},psiz[M]={0},p[M]={0},rec[M]={0},use=0; 11 12 void pushup(int x){siz[x]=siz[lc(x)]+siz[rc(x)]+1;psiz[x]=psiz[lc(x)]+psiz[rc(x)]+p[x];} 13 void rotate(int x,int &k){ 14 int y=fa[x],z=fa[y],l,r; 15 l=(ch[y][0]!=x); r=l^1; 16 if(y==k) k=x; 17 else{ 18 if(ch[z][0]==y) ch[z][0]=x; 19 else ch[z][1]=x; 20 } 21 fa[x]=z; fa[y]=x; fa[ch[x][r]]=y; 22 ch[y][l]=ch[x][r]; ch[x][r]=y; 23 pushup(y); pushup(x); 24 } 25 inline void splay(int x,int &k){ 26 while(x!=k){ 27 int y=fa[x],z=fa[y]; 28 if(y!=k){ 29 if((ch[y][0]==x)^(ch[z][0]==y)) rotate(x,k); 30 else rotate(y,k); 31 } 32 rotate(x,k); 33 } 34 } 35 int build(int l,int r,int f){ 36 if(l>r) return 0; 37 int mid=(l+r)>>1; fa[mid]=f; 38 lc(mid)=build(l,mid-1,mid); 39 rc(mid)=build(mid+1,r,mid); 40 pushup(mid); 41 return mid; 42 } 43 int find(int x,int k){ 44 if(siz[lc(x)]>=k) return find(lc(x),k); 45 if(siz[lc(x)]+1==k) return x; 46 return find(rc(x),k-siz[lc(x)]-1); 47 } 48 int findp(int x,int k){ 49 if(psiz[lc(x)]>=k) return findp(lc(x),k); 50 if(psiz[lc(x)]+p[x]==k) return x; 51 return findp(rc(x),k-psiz[lc(x)]-p[x]); 52 } 53 int getrank(int x){ 54 splay(x,root); 55 return siz[lc(x)]; 56 } 57 int split(int l,int r){ 58 int x=find(root,l),y=find(root,r+2); 59 splay(x,root); splay(y,ch[root][1]); 60 int res=lc(y); 61 lc(y)=0; 62 splay(y,root); 63 return res; 64 } 65 void ins(int k,int id){ 66 int x=find(root,k+1); 67 splay(x,root); 68 int y=rc(x); 69 while(lc(y)) y=lc(y); 70 lc(y)=id; fa[id]=y; 71 splay(lc(y),root); 72 } 73 void build(int nn){ 74 root=build(1,nn+1,0); 75 splay(1,root); 76 lc(1)=nn+2; siz[1]++; siz[nn+2]++; 77 } 78 }; 79 80 int a[M]={0}; 81 map<int,int> mp; vector<int> vt[M]; 82 83 namespace SAM{ 84 map<int,int> ch[M],son[M]; int l[M],fa[M],last=1,use=1,cnt=0; 85 int pos[M],ed[M],val[M],siz[M]; 86 void exc(int c,int id){ 87 int p=last,np=++use; l[np]=l[last]+1; last=np; 88 pos[np]=ed[np]=id; 89 for(;p&&ch[p][c]==0;p=fa[p]) ch[p][c]=np; 90 if(!p) fa[np]=1; 91 else{ 92 int q=ch[p][c]; 93 if(l[p]+1==l[q]) fa[np]=q; 94 else{ 95 int nq=++use; 96 l[nq]=l[p]+1; fa[nq]=fa[q]; 97 fa[q]=fa[np]=nq; ed[nq]=ed[q]; 98 ch[nq]=ch[q]; 99 for(int j=p;ch[j][c]==q;j=fa[j]) ch[j][c]=nq; 100 } 101 } 102 } 103 104 void build(){ 105 for(int i=n;i;i--) 106 exc(a[i],i); 107 for(int i=2;i<=use;i++){ 108 val[i]=a[ed[i]+l[fa[i]]]; 109 if(mp[val[i]]==0) mp[val[i]]=++cnt; 110 vt[mp[val[i]]].push_back(i); 111 son[fa[i]][val[i]]=i; 112 } 113 } 114 115 void dfs(int x){ 116 dfn[x]=++t; siz[x]=1; 117 H::rec[t]=x; 118 if(pos[x]) H::p[t]=1; 119 for(map<int,int>::iterator it=son[x].begin();it!=son[x].end();it++){ 120 dfs(it->second); 121 siz[x]+=siz[it->second]; 122 } 123 low[x]=t; 124 } 125 void updata(int ID){ 126 for(int i=0;i<vt[ID].size();i++){ 127 int id=vt[ID][i]; 128 int F=fa[id]; 129 int wei=H::getrank(dfn[F]); 130 int cutID=wei+siz[F]-siz[id]; 131 int P=H::split(cutID,cutID+siz[id]-1); 132 133 H::ins(wei,P); 134 } 135 } 136 }; 137 138 struct ask{ 139 int d,k,id; 140 ask(){d=k=id=0;} 141 void rd(int ID){id=ID; scanf("%d%d",&d,&k);} 142 friend bool operator <(ask a,ask b){return a.d<b.d;} 143 }Q[500005]; 144 145 int ans[500005]={0}; 146 147 int main(){ 148 // freopen("in.txt","r",stdin); 149 // freopen("out.txt","w",stdout); 150 scanf("%d%d%d",&n,&m,&q); 151 for(int i=1;i<=n;i++) scanf("%d",a+i); 152 153 SAM::build(); 154 SAM::dfs(1); 155 H::build(SAM::use); 156 157 for(int i=1;i<=q;i++) Q[i].rd(i); 158 sort(Q+1,Q+q+1); 159 sort(a+1,a+n+1); 160 int r=unique(a+1,a+n+1)-a-1,cnt=r; 161 162 for(int i=1;i<=q;i++){ 163 while(r&&a[r]+Q[i].d>=m){ 164 if(mp[a[r]]) 165 SAM::updata(mp[a[r]]); 166 r--; 167 } 168 int ID=H::findp(H::root,Q[i].k); 169 ans[Q[i].id]=SAM::pos[H::rec[ID]]; 170 } 171 for(int i=1;i<=q;i++) printf("%d\n",ans[i]); 172 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号