【2019北京集训2】Elephant 平衡树
题目大意:给你一个长度为$n$的序列$A_i$,有$q$次操作,每次操作为以下三种之一:
询问区间的$F_M(A_i)$的最大公约数。
区间翻转,区间加一个正数。
我们定义$gcd(0,0)=0$,且$F_M(A_i)$为在一个$M$个点的无向完全图中从第一个点开始走$k$步后回到第一个点的方案数。
数据范围:$n,q≤10^5$,$0≤A_i≤10^8$,$2≤M≤10^9$。
我们先考虑下如何求$F_M(x)$。
经过打表(大雾),我们发现:
若$x$为偶数,则$F_M(x)=M\times(F_M(x-1)+1)$
若$x$为奇数,则$F_M(x)=M\times(F_M(x-1)-1)$
特别地,$F_M(0)=1$,$F_M(1)=0$
我们显然可以$O(2\times 10^8)$预处理或者直接矩阵快速幂计算。
继续打表,我们发现:$gcd(F_M(x-1),F_M(y-1))=F_M(gcd(x-1,y-1))$,感兴趣的同学可以证明一下(反正我不会)
我们发现,如果询问的区间中存在数字0,则这个区间的GCD显然为1
考虑到要资瓷区间翻转,区间查询0的个数,区间抹去0,对于这部分我们需要单独开一棵splay来维护。
考虑维护>1部分的数。
我们先不考虑翻转的情况。
我们将差分后的数列丢入一棵splay中,每个节点维护整棵子树内的权值和,还有子树内的GCD
我们需要查询区间$[l,r]$的$GCD$时,我们只需要查询$[l+1,r]$的区间GCD,然后再和第$l$个位置的值求GCD即可输出。
原因显然
考虑翻转区间$[l,r]$的情况:不难发现受到影响的区间为$[l,r+1]$。
然后,经过冷静分析(大雾),我们发现翻转前后有这样的性质:
1,第$l$个位置的查分值和第$r+1$个位置的差分值需要单独更新。
2,区间$[l+1,r]$内的差分值等于原区间$[l+1,r]$内的差分值翻转再取相反数。
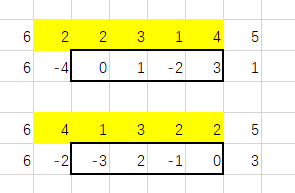
上面这张图是一个例子,证明显然。
然后,我们开几个标记打一下就可以了。
然后就没有然后了,注意细节
时间复杂度:$O(n\log^2\ n)$
1 #include<bits/stdc++.h> 2 #define M 200005 3 #define MOD 323232323 4 #define L long long 5 #define lc(x) ch[(x)][0] 6 #define rc(x) ch[(x)][1] 7 using namespace std; 8 9 int GCD(int x,int y){return __gcd(abs(x),abs(y));} 10 11 struct mat{ 12 L a[3][3]; mat(){memset(a,0,sizeof(a));} 13 void danwei(){a[0][0]=a[1][1]=a[2][2]=1;} 14 friend mat operator *(mat a,mat b){ 15 mat c; 16 for(int i=0;i<3;i++) 17 for(int j=0;j<3;j++) 18 for(int k=0;k<3;k++) 19 c.a[i][j]=(c.a[i][j]+a.a[i][k]*b.a[k][j])%MOD; 20 return c; 21 } 22 friend mat operator ^(mat x,int b){ 23 mat ans; ans.danwei(); 24 while(b){ 25 if(b&1) ans=ans*x; 26 x=x*x; b>>=1; 27 } 28 return ans; 29 } 30 }; 31 L P; 32 L getans(int n){ 33 if(n==0) return 0; 34 mat a; 35 a.a[0][1]=a.a[2][2]=1; 36 a.a[1][0]=P*P%MOD; 37 a.a[2][0]=(P-1+MOD)%MOD; 38 a=a^(n-1); 39 L res=a.a[2][0]*P%MOD; 40 if(n&1) res=P*(res+1)%MOD; 41 return res; 42 } 43 44 namespace FF{ 45 int siz[M]={0},ch[M][2]={0},sum[M]={0},tagf[M]={0},val[M]={0},rev[M]={0},fa[M]={0},use=0; 46 47 int root=0; 48 void pushup(int x){ 49 siz[x]=siz[lc(x)]+siz[rc(x)]+1; 50 sum[x]=sum[lc(x)]+sum[rc(x)]+val[x]; 51 } 52 void upd(int x){rev[x]^=1; swap(lc(x),rc(x)); } 53 void cls(int x){tagf[x]=1; sum[x]=val[x]=0;} 54 void pushdown(int x){ 55 if(rev[x]) upd(lc(x)),upd(rc(x)); rev[x]=0; 56 if(tagf[x]) cls(lc(x)),cls(rc(x)); tagf[x]=0; 57 } 58 void rotate(int x,int &k){ 59 int y=fa[x],z=fa[y],l,r; 60 l=(ch[y][0]!=x); r=l^1; 61 if(y==k) k=x; 62 else{ 63 if(lc(z)==y) ch[z][0]=x; 64 else ch[z][1]=x; 65 } 66 fa[y]=x; fa[x]=z; fa[ch[x][r]]=y; 67 ch[y][l]=ch[x][r]; ch[x][r]=y; 68 pushup(y); pushup(x); 69 } 70 void pud(int x,int k){if(x!=k) pud(fa[x],k); pushdown(x);} 71 72 void splay(int x,int &k){ 73 pud(x,k); 74 while(x!=k){ 75 int y=fa[x],z=fa[y]; 76 if(y!=k){ 77 if((lc(y)==x)==(lc(z)==y)) rotate(y,k); 78 else rotate(x,k); 79 } 80 rotate(x,k); 81 } 82 } 83 int insert(int x,int id,int zhi){ 84 pushdown(x); 85 if(!x){x=++use; val[x]=zhi;} 86 else{ 87 if(siz[lc(x)]+1<=id) rc(x)=insert(rc(x),id-siz[lc(x)]-1,zhi),fa[rc(x)]=x; 88 else lc(x)=insert(lc(x),id,zhi),fa[lc(x)]=x; 89 } 90 pushup(x); return x; 91 } 92 int find(int x,int k){ 93 pushdown(x); 94 if(siz[lc(x)]+1==k) return x; 95 if(siz[lc(x)]>=k) return find(lc(x),k); 96 return find(rc(x),k-siz[lc(x)]-1); 97 } 98 void ins(int x,int k){ 99 root=insert(root,k,x); 100 splay(use,root); 101 } 102 103 int query(int x,int y){ 104 int X=find(root,x),Y=find(root,y+2); 105 splay(X,root); splay(Y,rc(root)); 106 return sum[lc(Y)]; 107 } 108 void updata(int x,int y){ 109 int X=find(root,x),Y=find(root,y+2); 110 splay(X,root); splay(Y,rc(root)); 111 cls(lc(Y)); 112 pushup(Y); 113 pushup(root); 114 } 115 void setrev(int x,int y){ 116 int X=find(root,x),Y=find(root,y+2); 117 splay(X,root); splay(Y,rc(root)); 118 upd(lc(Y)); 119 } 120 } 121 122 int siz[M]={0},ch[M][2]={0},gcd[M]={0},sum[M]={0},val[M]={0},rev[M]={0},fa[M]={0},use=0; 123 124 int root=0; 125 void pushup(int x){ 126 siz[x]=siz[lc(x)]+siz[rc(x)]+1; 127 sum[x]=sum[lc(x)]+sum[rc(x)]+val[x]; 128 gcd[x]=GCD(GCD(gcd[lc(x)],gcd[rc(x)]),val[x]); 129 } 130 void upd(int x){rev[x]^=1; swap(lc(x),rc(x)); sum[x]=-sum[x]; val[x]=-val[x];} 131 void pushdown(int x){if(rev[x]) upd(lc(x)),upd(rc(x)); rev[x]=0;} 132 void rotate(int x,int &k){ 133 int y=fa[x],z=fa[y],l,r; 134 l=(ch[y][0]!=x); r=l^1; 135 if(y==k) k=x; 136 else{ 137 if(lc(z)==y) ch[z][0]=x; 138 else ch[z][1]=x; 139 } 140 fa[y]=x; fa[x]=z; fa[ch[x][r]]=y; 141 ch[y][l]=ch[x][r]; ch[x][r]=y; 142 pushup(y); pushup(x); 143 } 144 void pud(int x){if(x!=root) pud(fa[x]); pushdown(x);} 145 146 void splay(int x,int &k){ 147 pud(x); 148 while(x!=k){ 149 int y=fa[x],z=fa[y]; 150 if(y!=k){ 151 if((lc(y)==x)==(lc(z)==y)) rotate(y,k); 152 else rotate(x,k); 153 } 154 rotate(x,k); 155 } 156 } 157 int insert(int x,int id,int zhi){ 158 pushdown(x); 159 if(!x){x=++use; val[x]=zhi;} 160 else{ 161 if(siz[lc(x)]+1<=id) rc(x)=insert(rc(x),id-siz[lc(x)]-1,zhi),fa[rc(x)]=x; 162 else lc(x)=insert(lc(x),id,zhi),fa[lc(x)]=x; 163 } 164 pushup(x); return x; 165 } 166 int find(int x,int k){ 167 pushdown(x); 168 if(siz[lc(x)]+1==k) return x; 169 if(siz[lc(x)]>=k) return find(lc(x),k); 170 return find(rc(x),k-siz[lc(x)]-1); 171 } 172 void ins(int x,int k){ 173 root=insert(root,k,x); 174 splay(use,root); 175 } 176 void del(int k){ 177 int x=find(root,k); splay(x,root); 178 int y=find(root,k+1); lc(y)=lc(x); 179 fa[lc(x)]=y; fa[rc(x)]=0; root=rc(x); 180 splay(y,root); 181 182 } 183 184 int getval(int id){ 185 int x=find(root,id+1); 186 splay(x,root); 187 return val[x]+sum[lc(x)]; 188 } 189 int query(int x,int y){ 190 if(x>y) return 0; 191 int X=find(root,x),Y=find(root,y+2); 192 splay(X,root); 193 splay(Y,rc(root)); 194 return gcd[lc(Y)]; 195 } 196 void updata(int id,int delta){ 197 int x=find(root,id); 198 splay(x,root); 199 val[x]+=delta; 200 pushup(x); 201 } 202 203 void setrev(int x,int y){ 204 int X=find(root,x),Y=find(root,y+2); 205 splay(X,root); 206 splay(Y,rc(root)); 207 upd(lc(Y)); 208 pushup(lc(Y)); 209 splay(lc(Y),root); 210 } 211 212 void setval(int x,int V){ 213 int X=find(root,x+1); 214 splay(X,root); 215 val[X]=V; 216 pushup(X); 217 } 218 219 int n,m,a[M]={0}; 220 221 int main(){ 222 ins(0,0); ins(0,0); 223 FF::ins(0,0); FF::ins(0,0); 224 int cas; scanf("%d",&cas); 225 scanf("%d%d%d",&P,&n,&m); P--; 226 for(int i=1;i<=n;i++) scanf("%d",a+i),a[i]--; 227 228 for(int i=1;i<=n+1;i++){ 229 ins(a[i]-a[i-1],i); 230 FF::ins(a[i]==-1,i); 231 } 232 233 while(m--){ 234 int op,x,y; 235 scanf("%d%d%d",&op,&x,&y); 236 if(op==1){ 237 int F=FF::query(x,y); 238 if(F) {printf("1\n"); continue;} 239 int ans=query(x+1,y); 240 int las=getval(x); 241 printf("%lld\n",getans(GCD(las,ans))); 242 } 243 if(op==3){ 244 int k; scanf("%d",&k); 245 updata(x+1,k); 246 updata(y+2,-k); 247 FF::updata(x,y); 248 } 249 if(op==2){ 250 if(x==y) continue; 251 int Vl=getval(x-1); 252 int VR=getval(y); 253 int Vr=getval(y+1); 254 setrev(x+1,y); 255 FF::setrev(x,y); 256 setval(x,VR-Vl); 257 258 VR=getval(y); 259 260 setval(y+1,Vr-VR); 261 } 262 } 263 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号