【xsy1504】 pitcure 树状数组

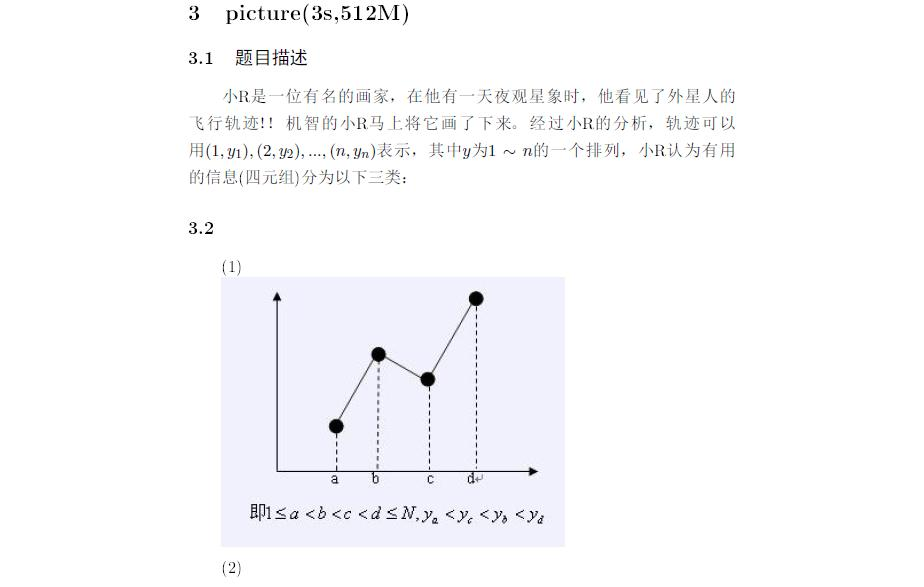
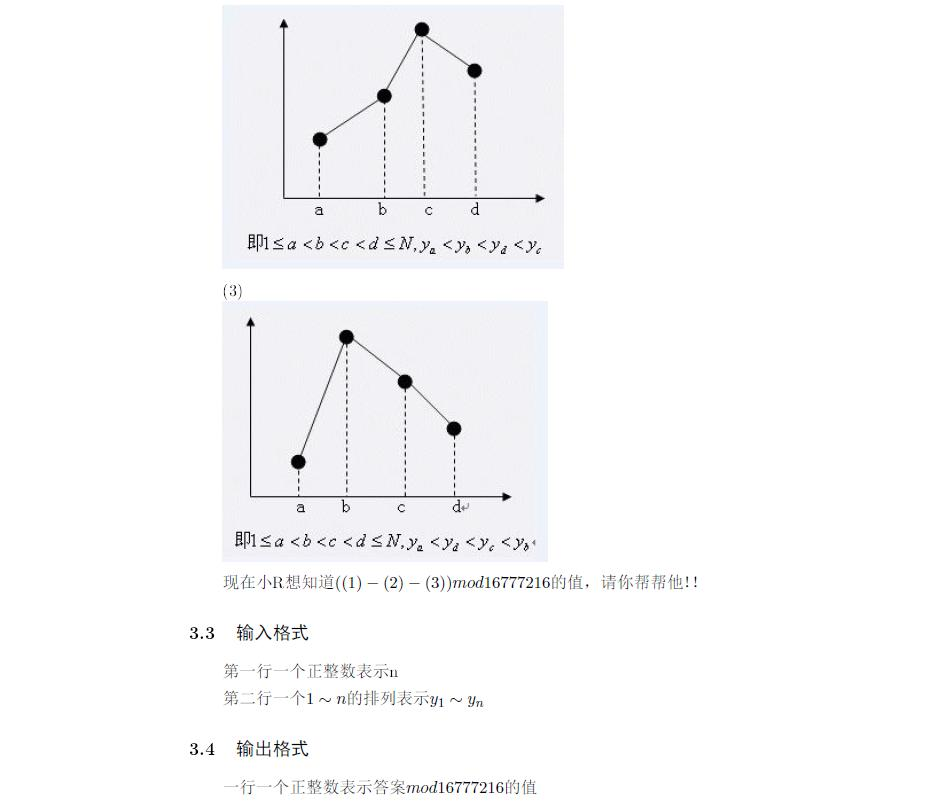
数据范围： $n≤2\times 10^5$

以下是题解：

 1 #include<bits/stdc++.h>
 2 #define L unsigned int
 3 #define MOD 16777216
 4 #define lowbit(x) ((x)&(-(x)))
 5 #define M 200005
 6 using namespace std;
 7 
 8 L b[M]={0},a[M]={0},n;
 9 void add(L x,L k){for(L i=x;i<=n;i+=lowbit(i)) b[i]+=k;}
10 L query(L x){L k=0; for(L i=x;i;i-=lowbit(i)) k+=b[i]; return k;}
11 
12 L solve1(){
13     static L r[M]={0},j[M]={0}; L res=0;
14     memset(b,0,sizeof(b));
15     for(L i=n;i;i--){
16         r[i]=query(n)-query(a[i]);
17         add(a[i],1);
18     }
19     memset(b,0,sizeof(b));
20     for(L i=1;i<=n;i++){
21         j[i]=query(a[i]);
22         add(a[i],i);
23     }
24     memset(b,0,sizeof(b));
25     for(L i=1;i<=n;i++){
26         L l=query(a[i]),now=0;
27         now+=1LL*l*(i-1);
28         now-=1LL*l*(l-1)/2;
29         now-=j[i];
30         res+=1LL*now*r[i];
31         add(a[i],1);
32     }
33     return res;
34 }
35 L solve2(){
36     static L r[M]={0},j[M]={0}; L res=0;
37     memset(b,0,sizeof(b));
38     for(L i=n;i;i--){
39         r[i]=query(n)-query(a[i]);
40         add(a[i],1);
41     }
42     memset(b,0,sizeof(b));
43     for(L i=1;i<=n;i++){
44         j[i]=query(a[i]);
45         add(a[i],a[i]);
46     }
47     memset(b,0,sizeof(b));
48     for(L i=1;i<=n;i++){
49         L l=query(a[i]),now=0;
50         now+=1LL*l*(a[i]-1);
51         now-=1LL*l*(l-1)/2;
52         now-=j[i];
53         res+=1LL*now*r[i];
54         add(a[i],1);
55     }
56     return res;
57 }
58     
59 L solve3(){
60     L res=0; memset(b,0,sizeof(b));
61     for(L i=n;i;i--){
62         L hh=query(n)-query(a[i]);
63         res+=(1LL*hh*(hh-1)*(hh-2)/6);
64         add(a[i],1);
65     }
66     return res;
67 }
68 L solve4(){
69     static L f[M]={0};
70     for(L i=n;i;i--) f[i]=1;
71     for(L x=1;x<=3;x++){
72         memset(b,0,sizeof(b));
73         for(L i=n;i;i--){
74             L hh=query(n)-query(a[i]);
75             add(a[i],f[i]);
76             f[i]=hh;
77         }
78     }
79     L res=0; for(L i=1;i<=n;i++) res+=f[i];
80     return res;
81 }
82 
83 main(){
84     scanf("%u",&n);
85     for(L i=1;i<=n;i++) scanf("%u",a+i);
86     L res1=solve1();//1x2x
87     L res2=solve2();//14xx
88     L res3=solve3();//1xxx
89     L res4=solve4();//1234
90     printf("%u\n",((res1+res2-res3+res4)%MOD+MOD)%MOD);
91 }