通俗易懂理解“万向锁”

网上关于万向锁的解释实在难以理解，摸索一番后有了比较直观的思考，记录如下：

在三维空间中表示旋转有4种方式：欧拉角，轴角旋转，旋转矩阵，四元数。

万向锁，是用欧拉角表示旋转时产生的一种问题，这个问题是可以解决的，只是很麻烦。

首先，欧拉角的旋转遵循一个顺序，比如x-y-z，y-x-z，x-y-x...  只要不是连续2个轴连着就可以，共有12种旋转顺序。

其次，旋转欧拉角的方式有两种，一种是绕着世界坐标系旋转，也叫“外旋”；另一种是绕着物体本身的局部坐标系转，也叫“内旋”，内旋的本质是先旋转坐标轴，再旋转点，由于我们最终描述点的位置是在世界坐标系上，因此内旋最终会转换为外旋，具体转换公式参考欧拉角旋转矩阵内外旋的等价性 - 简书 (jianshu.com)

这里理解内旋和外旋的关系至关重要，为了讲明白，举一个简单的例子：

有一架飞行中的飞机，我们在机头画一个点，不管飞机如何内旋yaw-roll-picth，最终我们需要知道的是这个点在世界坐标下的位置。由此可见，内旋只是方便操作的一种方式（对于飞机来说方便飞行员操作），但最终还是要转成外旋计算。

万向锁产生的原因，跟选项顺序和旋转方式（内旋-外旋）密切相关，也跟我们期望有关。

我们期望的是：

1.在世界坐标系中，旋转能有3个自由度，也就是在外旋看来，x/y/z三个方向都能旋转，这个是毋庸置疑的；

2.内旋的表示，转换成外旋也能有3个自由度，这在绝大部分情况下都是成立的，而极少的情况即“万向锁”。

我们以Unity的内旋(Local)为例，它的旋转顺序是y-x-z：

 

 

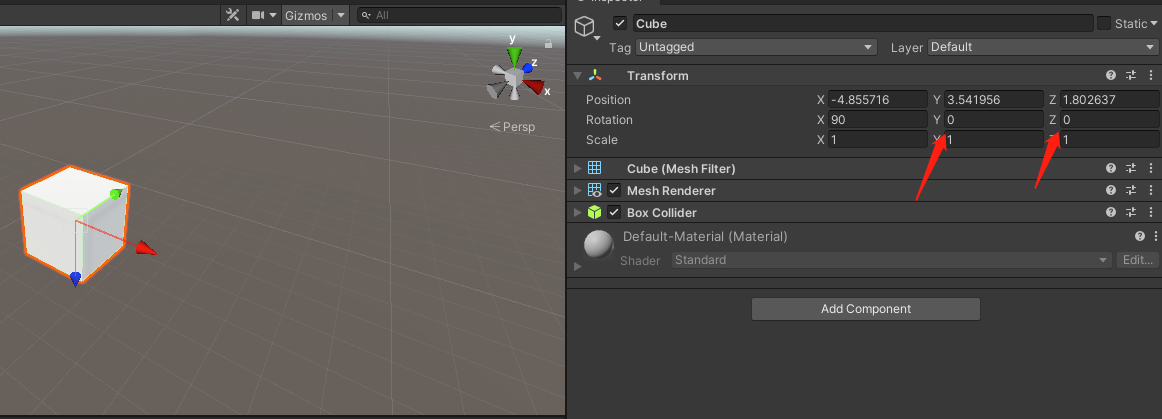
当我们内旋Ry(0°)Rx(90°)Rz(0°)时，即把中间的坐标轴x旋转了90°后，发生了这样的现象：

旋转前：局部y轴与世界y轴重合，局部x轴与世界x轴重合，局部z轴与世界z轴重合；

旋转后：局部y轴与世界z轴重合，局部x轴与世界x轴重合，局部z轴与世界y轴重合；

于是问题产生了：

先内旋y轴，这时旋转的是世界坐标系y轴 -> 再内旋x轴，局部坐标系的z轴变成了世界坐标系的y轴 -> 最后内旋z轴，旋转的是世界坐标系的y轴

 

 

 

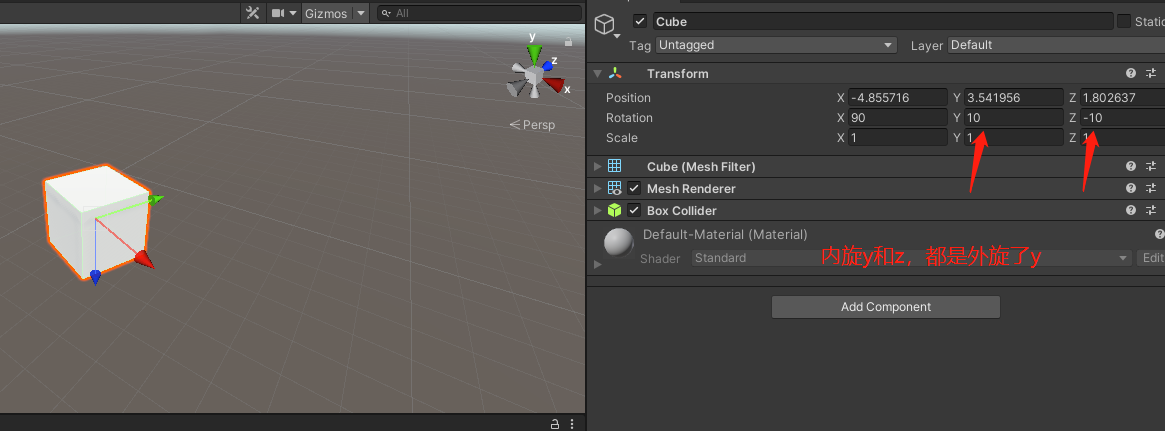
发现了吗！当中间x轴被内旋90°时，无论内旋y或内旋z，实际上都是外旋了世界坐标系的y轴，而世界坐标系的z轴，根本无法被旋转！

那么要如何才能使世界坐标系的z轴旋转呢？有2种方式：

1.x轴和z轴也额外旋转-90°，即Ry(-90°)Rx(90°)Rz(-90°)等价于Ry(0°)Rx(90°)Rz(0°)；

 

 

 

 

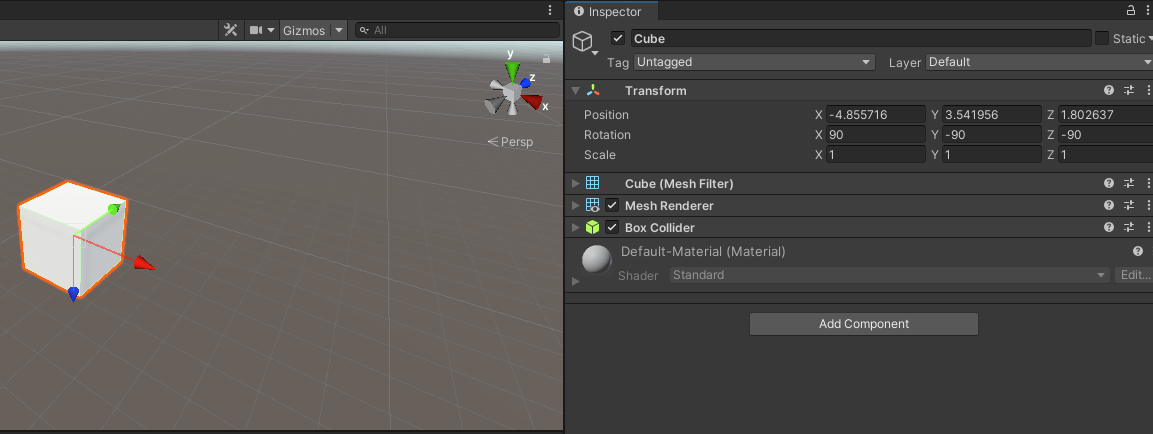
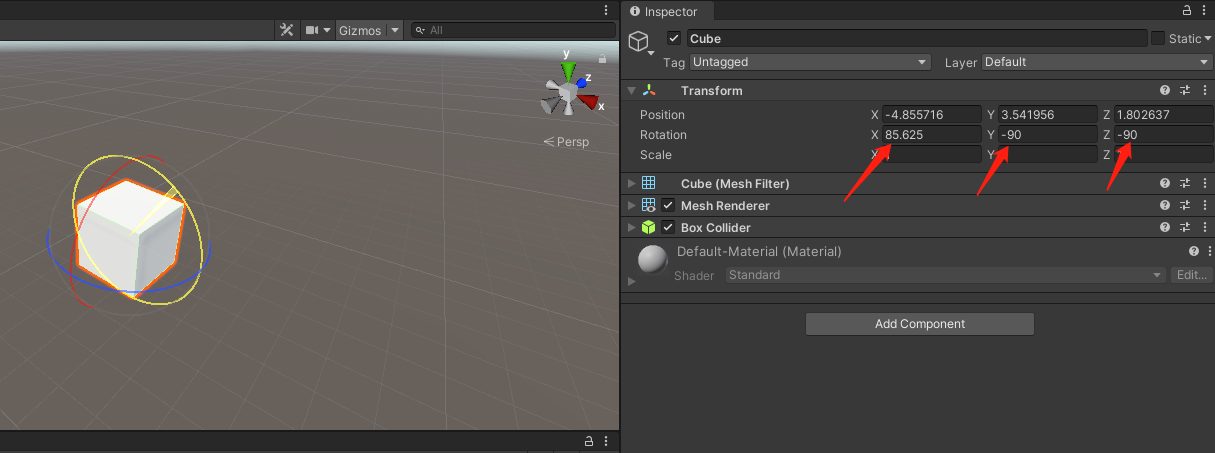
2.当x轴内旋为90°时，旋转顺序改成y-x-y。

无论哪种方式，都要处理临界点，在诸如插值等需要动态调整欧拉角时及其不便利。

总结：

万向锁是用欧拉角表示旋转时，内旋必然会产生的问题，表现为在外旋（世界坐标系）上少了一个旋转自由度，解决方法是处理临界点。用欧拉角表示静态的“朝向”是没有问题的，只是用在插值等动态变化的旋转时会有极大的不便。