图形学-光线追踪-空间划分

一般场景中的模型都是由三角形构成的，且数量非常多；同样用光线追踪的方式计算着色，由于光线会经过反射、折射等，光线的数量也非常多。 那么，如果简单粗暴的遍历计算所有的光线与所有三角形是否相交，计算量将大得惊人。

于是人们想到用空间划分的方式解决这个难题，即把整个场景空间划分成很多区域，先计算光线是否与这些区域相交，如果相交再计算光线是否与这些区域中的三角形相交。这里的空间指的是包裹着整个场景或某些物体的范围，叫做包围盒，基于直角坐标系为了计算简单一般用轴对称包围盒，也叫AABB。

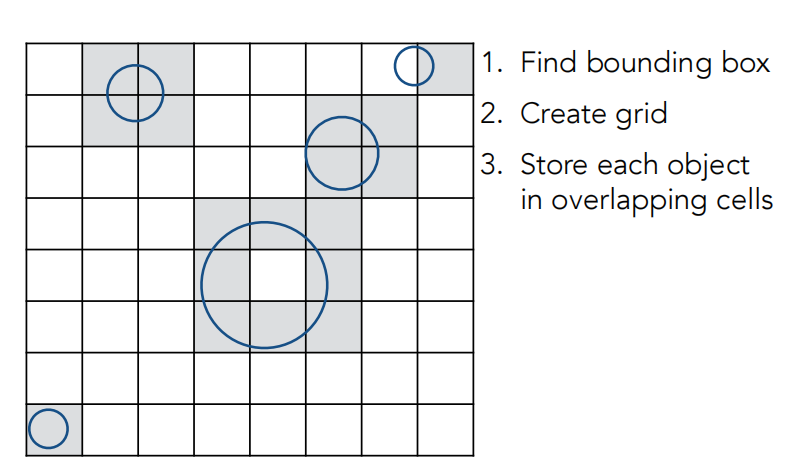
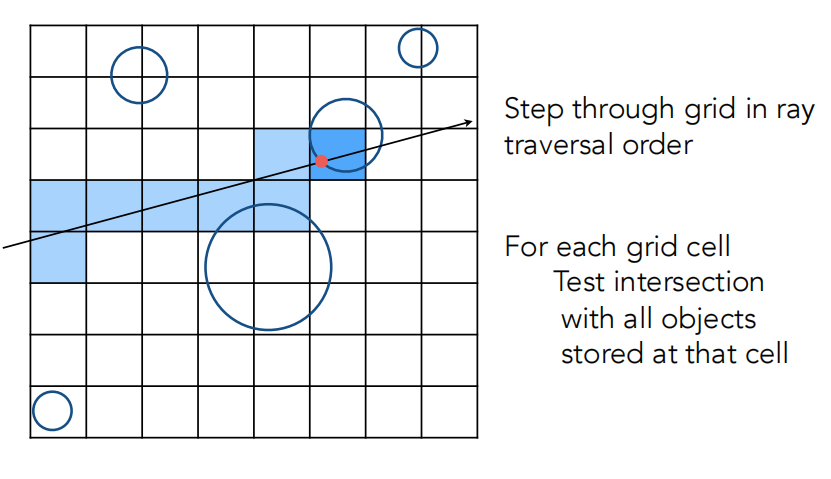
具体步骤如下：

1.找到所有物体的包围盒；

2.把包围盒分割成均匀的小格子；

3.找到每个格子包含哪些物体；

4.计算光线经过的格子，如果格子中包含物体，则求光线和物体（三角面）是否相交。

优化

简单分格子的空间划分确实能降低计算复杂度，但对于大片空出的场景，会出现“茶壶在运动场”问题。

 

如图所示，光线会与大量空白格子计算求交，做了很多无用功。我们希望能在有物体的区域才做空间划分。

 

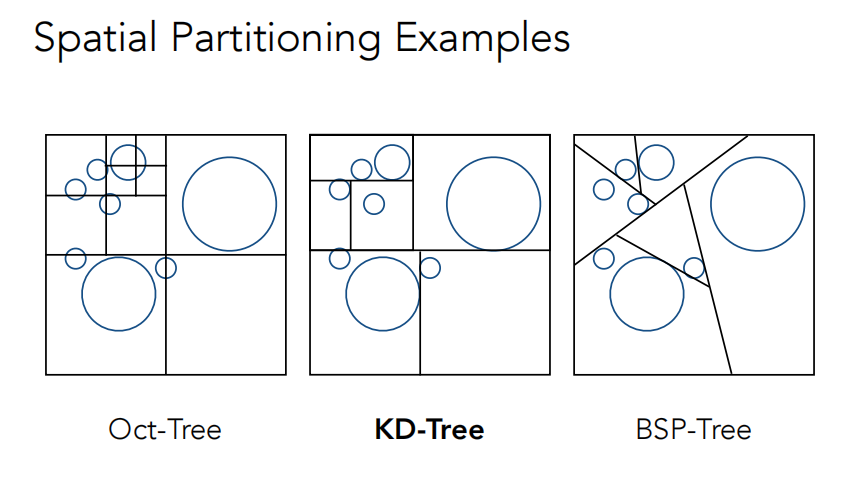
基于先不要一次性划分，而是先判断空间中是否有物体，再逐步划分的思想，人们提出3种“更划算”的空间划分方式，对于的数据结构都是树：

Oct-Tree：每次分4份（三维是8份，N维是2的N次方），用四叉树（三维是八叉树，N维是2的N次方叉数）表示；

KD-Tree：每次切一刀只分2份，下次再分2份，不断地分2份，每次沿着不同的轴分，如在三维空间中，先沿X轴分2份，再沿Y轴分2份，再沿Z轴分2份，再回到X轴分2份；

BSP-Tree：跟KD-Tree一样的分法，只是不平行与坐标轴分。

由KD-Tree相对容易计算，应用最广泛。

 

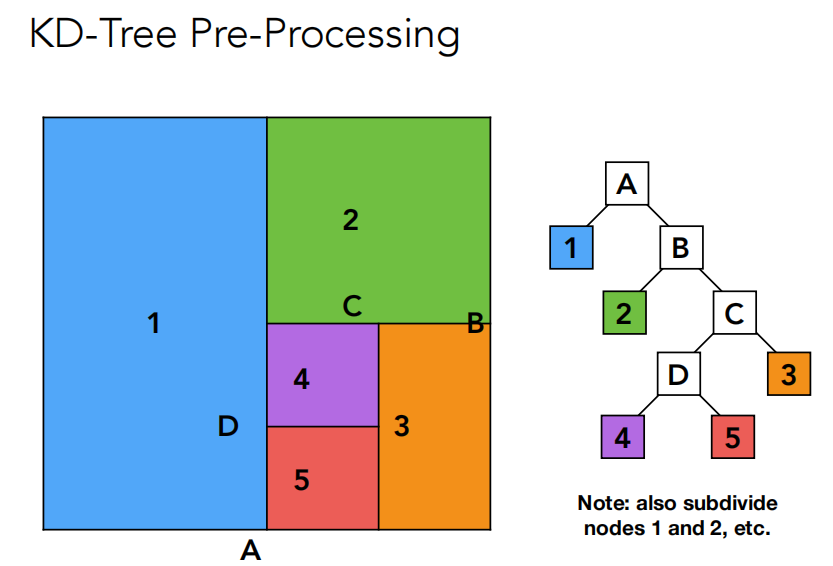
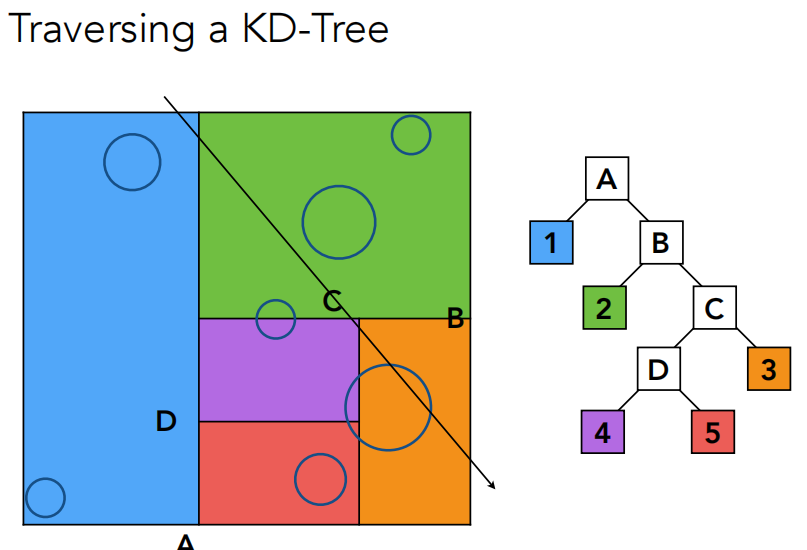
上图是KD-Tree的构建和光线求交判断。

基于空间的空间划分短板：

从上面KD-Tree的空间划分，我们会发现2个现象：

1.一个物体可能被多个空间“包含”，造成多次计算；

2.要判断一个物体是否在一个空间中不好计算，以三角形为例，我们可以认为三角形只要有1个顶点在空间中即判断为包含，但所有顶点都不在空间总并不能判断为不包含（有1个很小的格子在三角形内部）。

于是，我们要想一个方法规避上面的问题，即同一物体只会被一个空间包含，和比较容易判断物体是否在空间内。

基于物体的空间划分 Bounding Volume Hierarchy (BVH)

 

 

 

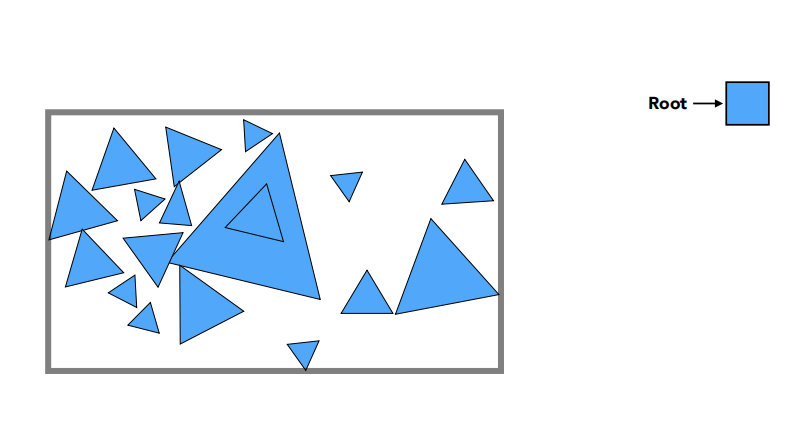
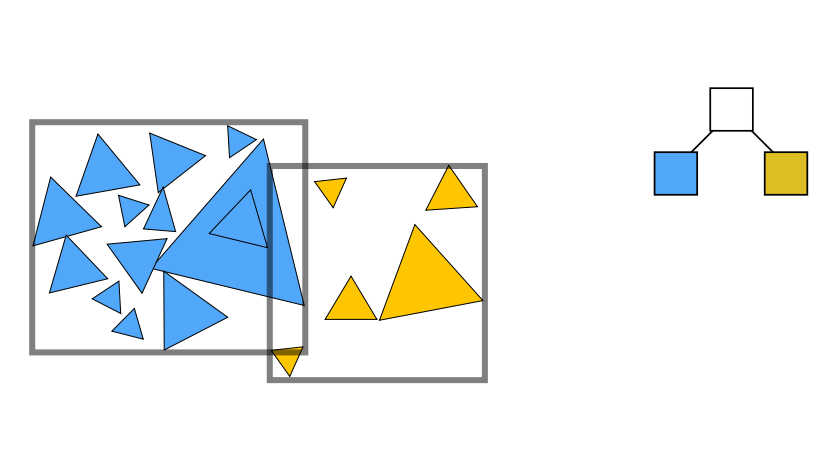
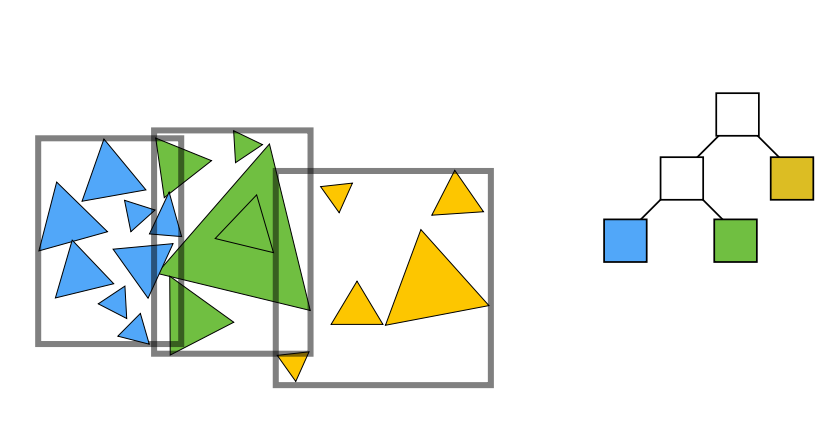
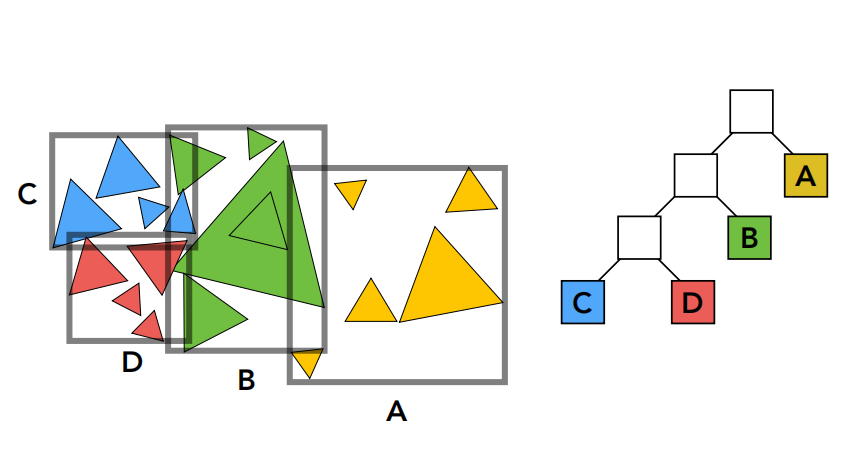
如图所示，我们把空间中的所有物体看做一个大家族，通过不断分家拆分成不同的空间，这样每个物体都在不同的空间中，在数据结构中则在不同的叶子节点中。

 

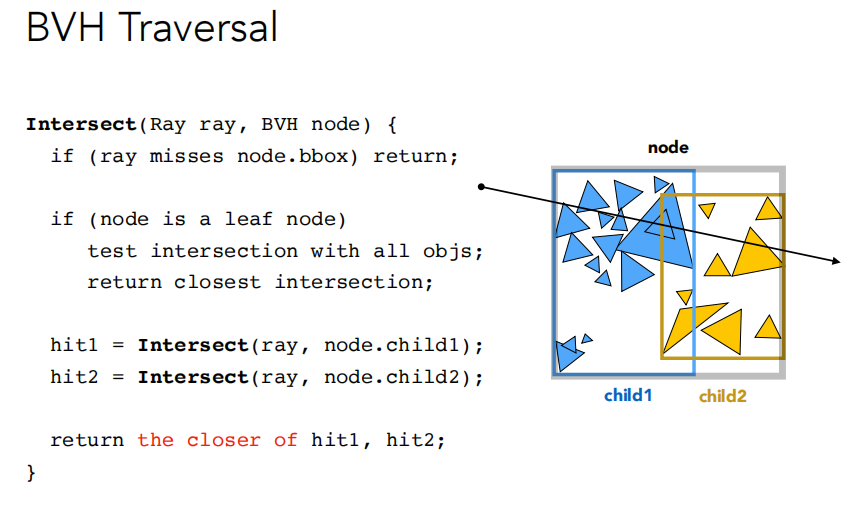
上图是这种“分家”算法的伪代码。 

这种空间划分算法的关键是如何找到拆分后的包围盒，因为如果包围盒太大，包含的物体数量过多，则查找效率上等于没有划分，还多出了几个相互重叠的空间。

 

空间划分在非图形学中的应用

其实空间划分不是图形学的专用技术，它是一种思想，在游戏的AOI上同样应用广泛。例如在魔兽世界的大地图上，可能同时10000人，10000人都在做不同的动作，不能同时把这10000人的信息同步给其余9999人，这就需要把一个大地图划分成不同的区域，并且动态的调整每个区域包含的玩家。