前缀和
1.1 一维前缀和
一维前缀和模板
package com.coedes.presum.mudel;
/**
* @description:一维前缀和
* @author: https://xuq7bkgch1.feishu.cn/docx/CAbedNJ5KobvinxdyKgcKsrlnrd
* @create: 2024/4/18 15:08
*/
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int N = 1000005;
int[] a = new int[N];
int[] S = new int[N];
int n = sc.nextInt();
int m = sc.nextInt();
for (int i = 1; i <= n; i++) {
a[i] = sc.nextInt();
S[i] = S[i - 1] + a[i];
}
while (m-- > 0) {
int l = sc.nextInt();
int r = sc.nextInt();
System.out.println(S[r] - S[l - 1]);
}
sc.close();
}
}
1.2 二维前缀和
二维前缀和模板
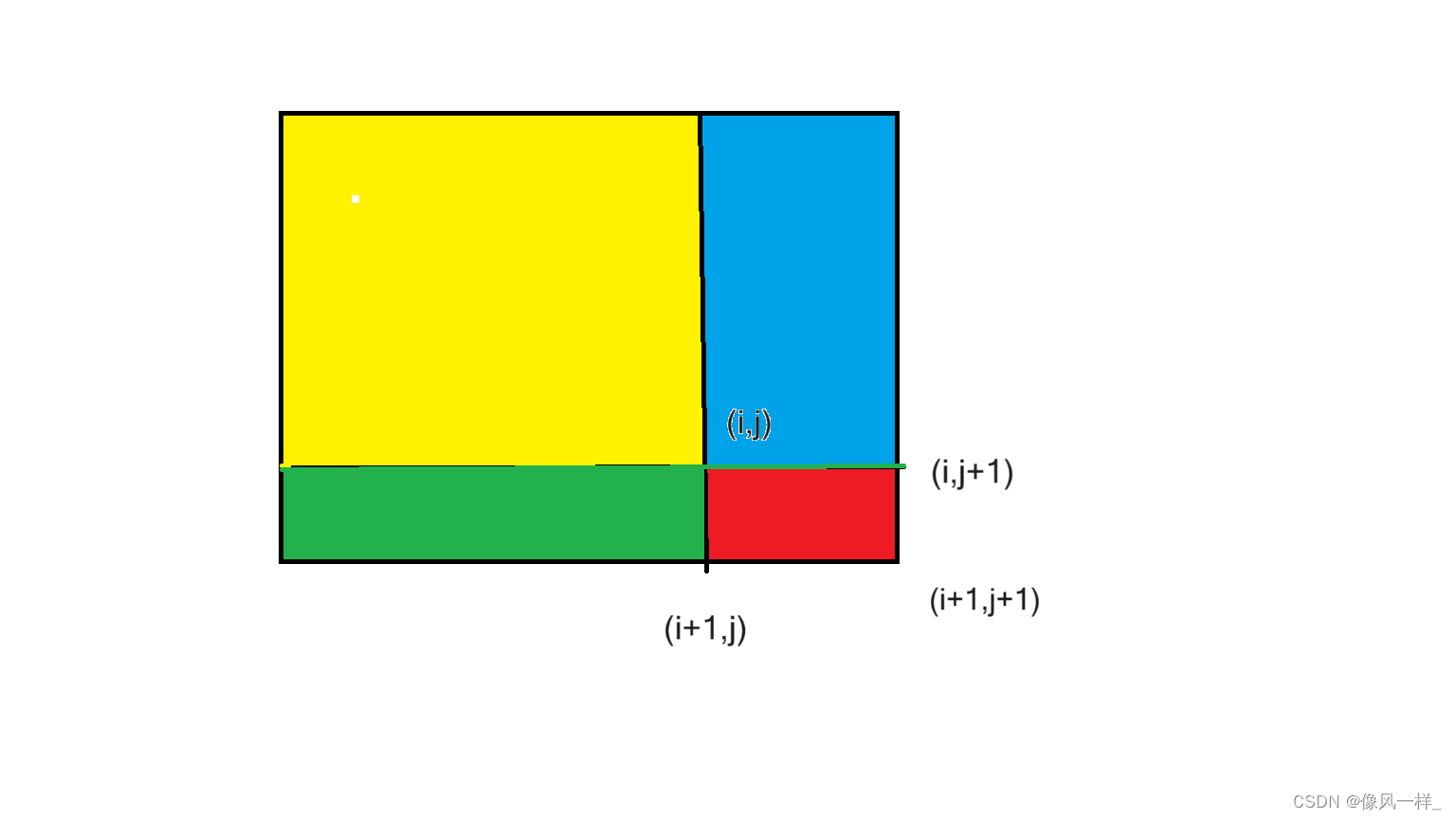
结合上述图形记忆。
/**
* @description:二维前缀和
* @author: https://xuq7bkgch1.feishu.cn/docx/CAbedNJ5KobvinxdyKgcKsrlnrd
* @create: 2024/4/18 15:08
*/
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner scan = new Scanner(System.in);
int n = scan.nextInt();
int m = scan.nextInt();
int q = scan.nextInt();
int[][] a = new int[n+1][m+1];
int[][] s = new int[n+1][m+1];
for(int i = 1 ; i <= n ; i ++ ){
for(int j = 1 ;j <= m ; j ++ ){
a[i][j] = scan.nextInt();
}
}
for(int i = 1 ; i <= n ; i ++ ){
for(int j = 1 ;j <= m ; j ++ ){
s[i][j] = s[i-1][j] + s[i][j-1] - s[i-1][j-1] + a[i][j];
}
}
while(q-->0){
int x1 = scan.nextInt();
int y1 = scan.nextInt();
int x2 = scan.nextInt();
int y2 = scan.nextInt();
System.out.println(s[x2][y2] - s[x1-1][y2] - s[x2][y1-1] + s[x1-1][y1-1]);
}
}
}
数组下标从 1 开始,可以减少很多边界问题的处理。
package com.coedes.presum.likou13;
/**
* @description:https://leetcode.cn/problems/O4NDxx/
* @author: wenLiu
* @create: 2024/4/15 12:33
*/
public class NumMatrix {
int dp[][];
public NumMatrix(int[][] matrix) {
int m = matrix.length + 1;
int n = matrix[0].length + 1;
dp = new int[m][n];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
dp[i][j] = matrix[i - 1][j - 1] + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
row1++;
col1++;
row2++;
col2++;
return dp[row2][col2] - dp[row2][col2-1] - dp[row2][col1 - 1] + dp[row1 - 1][col1 - 1];
}
}
2023 美团-塔子哥抓敌人-T3
- 游戏背景:塔子哥在虚拟游戏中控制角色,需要捕获尽可能多的敌人。
- 技能规则:一次性捕获的敌人在横坐标和纵坐标上有限制,横坐标差值不超过 A ,纵坐标差值不超过 B 。
- 目标:找出能被一次性捕获的最大数量的敌人,满足技能规则。
输入描述
第一行三个整数N,A,B,表示共有N个敌人,塔子哥的全屏技能的参数A和参数B。
接下来N行,每行两个数字x,y,描述一个敌人所在的坐标
1≤N≤500,1≤A,B≤1000,1≤x,y≤1000
输出描述
一行,一个整数表示塔子哥使用技能单次所可以捕获的最多数量。
样例11
输入
3 1 1 1 1 1 2 1 3
输出
2
题解
- **问题转化**:
- 限制矩形的长最多为 A+1 ,宽最多为 B+1 。
- 目标是找出在满足上述矩形限制条件下,矩形内元素之和的最大值,表示一次性捕获的最多敌人数量。
- **解决方法**:
- 使用二维前缀和:
- 构建 `prefixSum` 数组,其中 `prefixSum[i][j]` 表示从原点到 `(i, j)` 的矩形区域的元素之和。
- 遍历所有可能的矩形,通过前缀和数组快速计算矩形内元素之和。
- 检查满足技能规则的矩形,更新最大元素之和。
- **具体步骤**:
1. 构建 `prefixSum` 数组:
- `prefixSum[i][j]` 的计算方式为:`prefixSum[i][j] = matrix[i][j] + prefixSum[i-1][j] + prefixSum[i][j-1] - prefixSum[i-1][j-1]`。
2. 遍历所有可能的矩形:
- 对于每个 `(x1, y1)` 到 `(x2, y2)` 的矩形,利用前缀和数组快速计算矩形内元素之和。
3. 检查满足技能规则的矩形,并更新最大元素之和。
- **时间复杂度**:
- 由于坐标范围不超过 10^3 ,整体时间复杂度为 O(n^2) ,其中 n 是坐标的最大范围。
import java.util.*;
public class Main {
static int N = 1020;
static int[][] s = new int[N][N];
static int n, a, b;
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
a = scanner.nextInt();
b = scanner.nextInt();
for (int i = 0; i < n; i++) {
int x = scanner.nextInt();
int y = scanner.nextInt();
s[x][y]++;
}
for (int i = 1; i <= 1010; i++) {
for (int j = 1; j <= 1010; j++) {
// 计算前缀和
s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
}
}
int res = 0;
for (int x2 = a + 1; x2 <= 1010; x2++) { // 枚举矩形的右下角的横坐标
for (int y2 = b + 1; y2 <= 1010; y2++) { // 枚举矩形右下角的纵坐标
int x1 = x2 - a, y1 = y2 - b; // 矩形左上角的横纵坐标
// 求横坐标在[x1,x2] 纵坐标在[y1,y2]的元素个数
int cnt = s[x2][y2] - s[x2][y1 - 1] - s[x1 - 1][y2] + s[x1 - 1][y1 - 1];
res = Math.max(res, cnt);
}
}
System.out.println(res);
}
}
1.3 前缀和+哈希
使用场景:数组不满足单调性(即数组存在负数),求满足条件的子串/子数组个数。
例题:
LeetCode 930. 和相同的二元子数组
类似题型
LeetCode.560. 和为 K 的子数组
初始化哈希表时,将键 0 对应的值设为 1,表示空数组的情况。
class Solution {
// 前缀和+哈希
public int numSubarraysWithSum(int[] nums, int goal) {
int ret = 0;
HashMap<Integer, Integer> hashMap = new HashMap<>();
int sum = 0;
hashMap.put(0, 1);
for (int j = 0; j < nums.length; j++) {
sum += nums[j];
ret += hashMap.getOrDefault(sum - goal, 0);
hashMap.put(sum, hashMap.getOrDefault(sum, 0) + 1);
}
return ret;
}
}
LeetCode 1590. 使数组和能被 P 整除
%p的值为sum%p,如果不存在,返回-1
class Solution {
public int minSubarray(int[] nums, int p) {
//[3,1,4,2]
//[3,4,5,7]
//问题转化为找 和为sum%p的子数组 问题 => likoiu930 和相同的二元子数组
int ret = nums.length;
//存放 前缀和%p : 下标
HashMap<Long, Integer> hashMap = new HashMap<>();
long sum = 0;//求和都给long
for (int num : nums) {
sum += num;
}
if (sum%p==0) {
return 0;
}
long val = sum % p;
hashMap.put(0L, -1);
long s = 0;
for (int i = 0; i < nums.length; i++) {
//i+1~j 和 <=> s[i]-s[j] = val (sum%p)
s = (s+nums[i])%p;
// 注意取模问题:减法取模时,为了避免负数,要+p 因为 val = sum%p => 0< val < p => -val+p > 0
long target = (s - val + p) % p;
if (hashMap.containsKey(target)) {
ret = Math.min(ret,i-hashMap.get(target));
}
hashMap.put(s,i);
}
return ret==nums.length?-1:ret;
}
}
HDSF大学保研机试-2022-差分计数
给定n个整数a1,...,an和一个整数x。求有多少不同下标对(i,j)满足ai−aj=x。 (1, 5) 和 (5, 1) 不一样,但(1, 1) 和 (1, 1) 一样。
输入格式
第一行两个整数n,x。
第二行n个用空格隔开的整数,第i个代表−2×106≤ai≤2×106
输出格式
一行一个整数,代表满足ai−aj=x的不同下标对(i,j)个数。
样例
input
5 1 1 1 5 4 2
ouput
3
解题思路:桶预处理
方法一:先试试暴力解法,枚举所有二元组:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int x = in.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = in.nextInt();
}
int cnt = 0;
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (a[i] - a[j] == x || a[j]-a[i] == x) {
cnt++;
}
}
}
System.out.println(cnt);
}
}
超时了!
方法二:桶预处理(哈希来存)
 (图片来源于塔子哥https://codefun2000.com/p/P1050/solution)
(图片来源于塔子哥https://codefun2000.com/p/P1050/solution)
计算给定数组中满足条件 ai - aj = x 的不同下标对 (i, j) 的数量。使用哈希表来记录每个数组元素的出现次数,并利用差值 x 来寻找符合条件的配对。
处理差值时的顺序问题:对于 [1 1 5 4 2] 元素5加入但4不在map中 因此 答案(5,4)无法更新到结果,因此需要预处理。
import java.util.HashMap;
import java.util.Scanner;
/**
* @description:https://codefun2000.com/p/P1050
* @author: wenLiu
* @create: 2024/4/17 13:32
*/
public class Solution2 {
// 错误处理方法
/*public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int x = in.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = in.nextInt();
}
int cnt = 0;
//ai - aj = x aj = ai - x
//map 存放 {value : cnt}
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
if (map.containsKey(a[i] - x)) {
cnt += map.get(a[i] - x);
}
map.put(a[i], map.getOrDefault(a[i], 0) + 1);
}
System.out.println(cnt);
}*/
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int x = in.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = in.nextInt();
}
// 第二步:枚举每个数,统计答案
// 答案可能很大:考虑ai全等且x=0,那么任意两个i,j都是一个答案。那么答案会是n^2阶的。
// 尝试将其带进去会发现它爆int了,所以只能用long long 存储
long cnt = 0;
//ai - aj = x aj = ai - x
//map 存放 {value : cnt}
HashMap<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < n; i++) {
map.put(a[i], map.getOrDefault(a[i], 0) + 1);
}
for (int i = 0; i < n; i++) {
if (map.containsKey(a[i] - x)) {
cnt += map.get(a[i] - x);
}
}
System.out.println(cnt);
}
}
2023阿里-切割环形数组
题目内容
将环形数组 a 分割成两段,使得两段数字之和相等。在任意两个数字之间切割,但每段都不能为空。现在请求计算有多少种不同的切割方案可以达到这个目标。
输入描述
第一行输入一个正整数 n ,代表环形数组的元素数量。
第二行输入 n 个正整数 ai,代表环形数组的元素。
1≤n≤105
-109≤ai≤109
输出描述
一个整数,代表切割的方案数。
输入
5 1 4 -2 5 2
输出
2
解释下什么叫做“切两边”和“切中间”:
切两边 :1 4 | -2 5 2 或者 1 4 -2 | 5 2 => presum[i] = sum/2
切中间 :1 4 | -2 5 | 2 => [1,i] 有多少个满足区间(j,i)和为sum/2的个数
注意前缀和数组不能包括开始的0,防止出现不分割的情况
环形数组切割方式:切两边、切中间
1、切两边:满足presum[i] = sum/2 cnt++
2、切中间: 哈希记录前缀和值和出现次数,cnt+=s-sum/2.(计算数组(1,i)和为sum/2的子数组个数)
注意最后 i<n 不是 i<=n!
for (int i = 1; i < n; i++) {//切两边
for (int i = 1; i < n; i++) {//切中间
我们考虑切割出来的两段,如果某一段的最后一位数字是在中间,我们直接根据前缀和,计数+1即可,
如果切割出来的那一段的最后一位数字是数组的最后一个数字,那就说明已经在前面计数过一次了,就不要再加了,
比如1 ,4 ,| -2, 5, 2 (找到14的时候计数+1,找到-252的时候就不要计数了,因为14 和 -252是同一对)
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
long[] w = new long[n + 1];
long[] s = new long[n + 1];
for (int i = 1; i <= n; i++) {
w[i] = scanner.nextLong();
}
for (int i = 1; i <= n; i++) {
s[i] = s[i - 1] + w[i];
}
if (s[n] % 2 != 0) {
System.out.println("0");
} else {
long sum = s[n] / 2;
Map<Long, Long> cnts = new HashMap<>();
long res = 0;
for (int i = 1; i < n; i++) {//切两边
if (s[i] == sum) {
res++;
}
}
for (int i = 1; i < n; i++) {//切中间
res += cnts.getOrDefault(s[i] - sum, 0L);
cnts.put(s[i], cnts.getOrDefault(s[i], 0L) + 1);
}
System.out.println(res);
}
}
}
2023 美团-平均数
题目内容
给定一个正整数数组a1,a2,...an,求平均数正好等于k的最长连续子数组的长度
输入描述
第一行输入两个正整数n和k
第二行输入n个正整数ai,用来表示数组
1≤n≤1e5
1≤k,ai≤1e9
输出描述
输出一个整数,表示最长满足题目条件的长度。
样例
输入
5 2 1 3 2 4 1
输出
3
package com.coedes.presum.meituan2023T5;
import java.util.HashMap;
import java.util.Map;
import java.util.Scanner;
/**
* @description:https://codefun2000.com/p/P1497
* @author: wenLiu
* @create: 2024/4/17 20:55
*/
public class Main {
/*
下标从1开始,使用前缀和计算区间[1,i]的区间和s[i]。
对于以i结尾的区间,如果存在平均数为k的区间[j,i],
定义长度为len=i-j+1,满足 s[i] - s[j-1] = k * len。
化简后得到 s[i] - k * i = s[j-1] - (j - 1) * k。
枚举每个i时,只需检查哈希表中是否存在值s[i] - k * i。
若存在,则更新最大长度;否则,将(s[i] - k * i)和i存入哈希表。
*/
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int k = in.nextInt();
long[] a = new long[n + 1];
for (int i = 1; i <= n; i++) {
a[i] = in.nextLong();
}
long[] s = new long[n + 1];
for (int i = 1; i <= n; i++) {
s[i] = s[i - 1] + a[i];
}
long res = -1;
Map<Long, Integer> mp = new HashMap<Long, Integer>();
mp.put(0L, 0);//一开始初始化哈希表为mp[s[0] - 0 * k] = mp[0 - 0] = mp[0] = 0
for (int i = 1; i <= n; i++) {
long target = s[i] - k * i;
if (mp.containsKey(target)) {
res = Math.max(res, i - mp.get(target));
} else {
mp.put(target, i);
}
/*
不要因为前面思维惯性 这么写:
if (mp.containsKey(target)) {
res = Math.max(res, i - mp.get(target));
}
mp.put(target, i);
}
比如数组为a =[4, 3, 2, 5],k = 3,下标从1开始
一开始初始化哈希表为mp[s[0] - 0 * k] = mp[0 - 0] = mp[0] = 0
遍历到下标1,就是元素4的位置,计算数值s[1] - 1 * k = 4 - 3 = 1,
哈希表中不存在1,记录mp[1] = 1 后,跳过;
遍历到下标2,就是元素3的位置,计算数值s[2] - 2 * k = 4 + 3 - 2 * 3 = 1 ,
哈希表中存在1,更新最大长度res = max(res, i - mp[s[i] - k * i]) = max(res, 2 - 1) = 1 ,
也就是子数组【3】,找到了一个答案,此时不能put!不然原来map中{1:1} 被{1:2}覆盖 导致最大长度为2
*/
}
System.out.println(res);
}
}
做下面这道提前需要知道的前置知识:
LeetCode 1371. 每个元音包含偶数次的最长子字符串
先试试暴力解法...时间复杂度达到O(n3)...一定time out
对于给定的字符串 s,我们可以使用双重循环来枚举所有可能的子字符串,然后对每个子字符串进行统计元音字母出现次数的操作。具体步骤如下:
- 枚举所有可能的起始位置
start和结束位置end,其中start <= end。 - 对于每个子字符串
s[start:end+1],统计其中元音字母('a', 'e', 'i', 'o', 'u')出现的次数。 - 检查统计结果,看是否每个元音字母都出现了偶数次。
- 如果满足条件,更新最长子字符串的长度。
public class Solution{
// Helper function to check if all counts in the array are even
private boolean isEvenCount(int[] count) {
for (int c : count) {
if (c % 2 != 0) {
return false;
}
}
return true;
}
public int findTheLongestSubstring(String s) {
char[] vowels = {'a', 'e', 'i', 'o', 'u'};
int maxLen = 0;
int n = s.length();
for (int start = 0; start < n; start++) {
int[] count = new int[5]; // Array to count occurrences of 'a', 'e', 'i', 'o', 'u'
for (int end = start; end < n; end++) {
char ch = s.charAt(end);
for (int i = 0; i < vowels.length; i++) {
if (ch == vowels[i]) {
count[i]++;
break;
}
}
if (isEvenCount(count)) {
// If all counts are even, update the maximum length
maxLen = Math.max(maxLen, end - start + 1);
}
}
}
return maxLen;
}
}
还是看看力扣大佬写的题解吧...参考 作者:笨猪爆破组...问题转化为 [0,j] 的 state 等于 [0,i−1] 的 state,即两个二进制数相等。
package com.coedes.presum.likou1371;
import java.util.HashMap;
import java.util.Map;
/**
* @description:TODO
* @author: wenLiu
* @create: 2024/4/18 10:59
*/
public class Solution2 {
/*记录各个原音字母对应状态码 状态码存储方式为十进制
a 00001 1
e 00010 2
i 00100 4
o 01000 8
u 10000 16*/
static Map<Character, Integer> vowel = new HashMap<Character, Integer>() {
{
put('a', 1);
put('e', 2);
put('i', 4);
put('o', 8);
put('u', 16);
}
};
/**
* 返回元音字母长度为偶数的最长子字符串的长度
*
* @param s
* @return
*/
public int findTheLongestSubstring(String s) {
int res = -1;
//记录[1,i]出现的状态码和索引 {state:index}
HashMap<Integer, Integer> mp = new HashMap<>();
//令index = -1 aeiou个数都为0 故初始化 {0:-1} 同时可避免index=0的开头判断
mp.put(0, -1);
//记录状态的前缀异或和
int state = 0;
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (vowel.containsKey(c)) {
state ^= vowel.get(c);
//如果mp没有保存过当前状态则保存 因为要求最大距离 直接存取可能会把之前的index覆盖 和2023 美团-平均数中的else类似
if (!mp.containsKey(state)) {
mp.put(state, i);
}
}
res = Math.max(res, i - mp.get(state));
}
return res;
}
public static void main(String[] args) {
Solution2 solution = new Solution2();
System.out.println(solution.findTheLongestSubstring("bcbcbc"));
}
}
2023百度-魔法师
题目内容
将所有魔法元素排成一行,从左到右第 i 个魔法元素的能量值是一个非零整数 ai 。他发现,他可以选出一段连续的魔法元素,将它们的能量值乘起来得到一个总能量值。如果这个总能量值大于零,他就能施展出一种白魔法,否则他只能施展出黑魔法。
现在塔子哥想知道施展一个白魔法或黑魔法的方案数分别有多少。两个方案不同是指挑选的连续区间不同。
输入描述
第一行有一个整数 n ( 1≤n≤2×105 ),表示魔法元素的个数。
第二行有 n 个整数a1,a2,...,an ( −109≤ai≤109 ),代表魔法元素的能量值。
输出描述
输出两个整数,分别表示施展一个黑魔法和施展一个白魔法的方案数。
样例
输入
6 6 -1 -3 5 3 -5
输出
10 11
题解
6
6 -1 -3 5 3 -5
0 1 1 0 0 1
0⊕0=0
zeros:0+=1=>1
ones:0+=0=>0
cnts[0]:1=>2
0⊕1=1
zeros:1+=0=>1
ones:0+=2=>2
cnts[1]:0=>1
1⊕1=0
zeros:1+=2=>3
ones:2+=1=>3
cnts[0]:2=>3
0⊕0=0
zeros:3+=3=>6
ones:3+=1=>4
cnts[0]:3=>4
0⊕0=0
zeros:6+=4=>10
ones:4+=1=>5
cnts[0]:4=>5
0⊕1=1
zeros:10+=1=>11
ones:5+=5=>10
cnts[1]:1=>2
10 11
进程已结束,退出代码0
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int[] w = new int[n];
for (int i = 0; i < n; i++) {
w[i] = scanner.nextInt();
w[i] = (w[i] > 0) ? 0 : 1;
}
int[] cnts = new int[2];
cnts[0]=1;cnts[1]=0;
long zeros = 0, ones = 0;
int s = 0;
for (int i = 0; i < n; i++) {
s ^= w[i];
zeros += cnts[s];
ones += cnts[1 - s];
cnts[s]++;
}
System.out.println(ones + " " + zeros);
}
}
题解: 来自 https://xuq7bkgch1.feishu.cn/docx/CAbedNJ5KobvinxdyKgcKsrlnrd
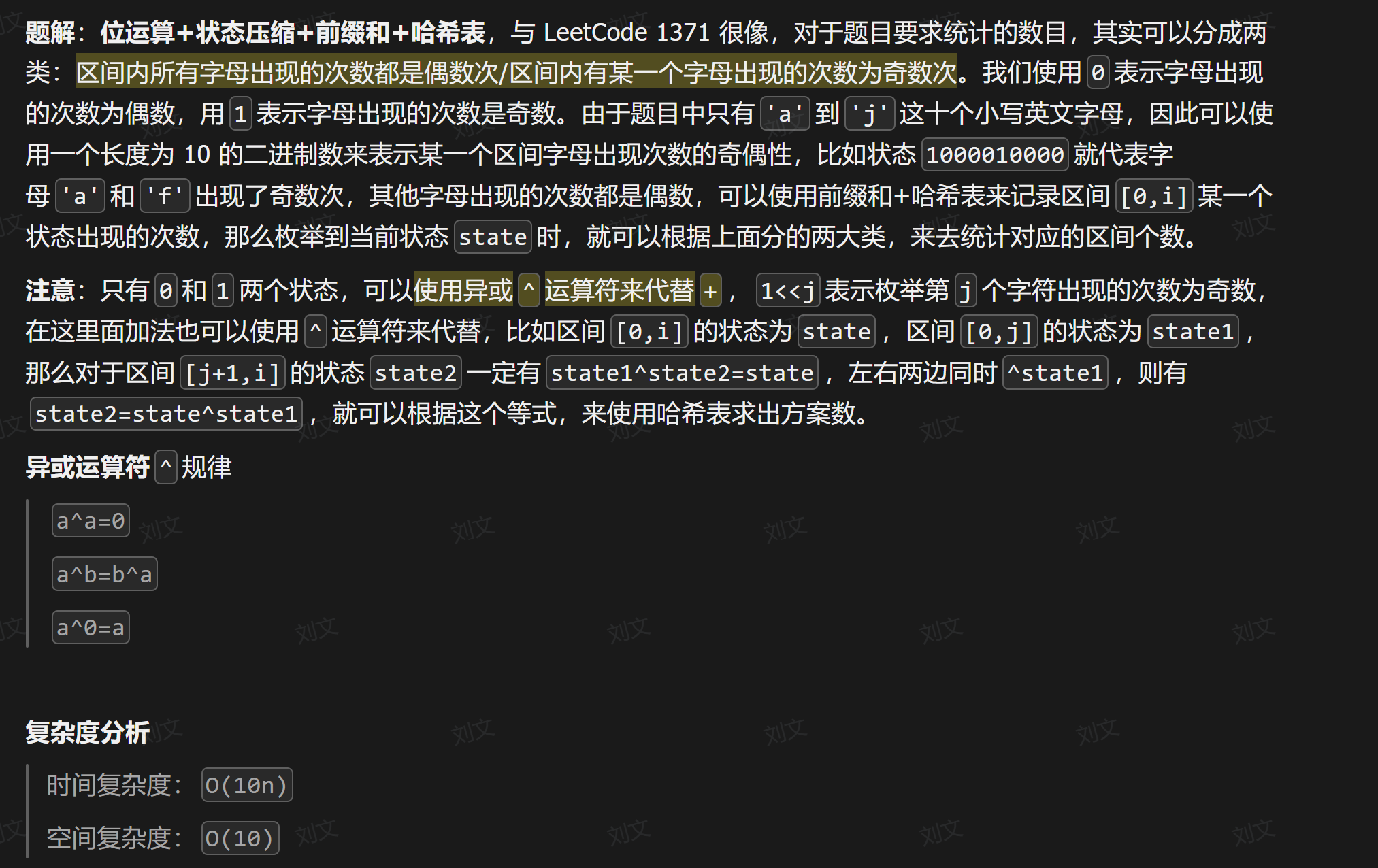
package com.coedes.presum.likou1915;
import java.util.HashMap;
import java.util.Map;
/**
* @description:题解来自 :https://leetcode.cn/problems/number-of-wonderful-substrings/solutions/846871/qian-zhui-he-chang-jian-ji-qiao-by-endle-t57t/
* @author: return up;
*/
public class Solution {
public long wonderfulSubstrings(String word) {
Map<Integer, Integer> cnt = new HashMap<>();
// 空字符串的前缀和为0,数量为1个
cnt.put(0, 1);
// 记录所有字符的前缀和
int pre = 0;
long res = 0;
for (char c : word) {
// 1<<i表示1左移i位,此时求出来的数值为当前前缀和
pre ^= 1 << (c - 'a');
// 加上所有出现偶数次的字符串的次数;
// 首先abb中的a对应二进制001,
// 遍历到第一个b时对应的二进制为011,
// 遍历到第二个b时,异或得到的二进制为001,也就是当前字符出现偶数次
res += cnt.getOrDefault(pre, 0);
// 枚举10个字符出现奇数次的情况
for (int i = 0; i < 10; ++i) {
// 某个字符出现奇数次,那么10位二进制数的第i位为1,也就是1<<i
// 设某位为1,其余位为0的前缀和为x,
// 那么x^pre=1<<i ==> x=(x^pre)^pre=(1<<i)^pre
// 也就是说某位1,其余位为0的前缀和x= (1<<i)^pre
res += cnt.getOrDefault((1 << i) ^ pre, 0);
}
// 更新当前的前缀和的次数
cnt.put(pre, cnt.getOrDefault(pre, 0) + 1);
}
return res;
}
}
1.3 前后缀分解
LeetCode 238. 除自身以外数组的乘积
解法一:除法解决(题目要求不能用除法!)
首先遍历数组计算总乘积 totalProduct 和零元素个数 zeroCount,
然后根据 zeroCount 的值填充结果数组 result。最后返回结果数组 result。
解法二:前后缀分解
1. **初始化**:
- 创建长度为 `n` 的数组 `res`、`l` 和 `r`,并将 `l` 和 `r` 的所有元素初始化为 1。
2. **计算前缀乘积**:
- 从左到右遍历数组 `nums`,用 `l` 数组存储到当前位置左侧所有元素的乘积。
3. **计算后缀乘积**:
- 从右到左遍历数组 `nums`,用 `r` 数组存储到当前位置右侧所有元素的乘积。
4. **计算结果**:
- 结合 `l` 和 `r` 数组,计算最终的结果数组 `res`,其中每个元素 `res[i]` 是其左侧元素乘积 (`l[i]`) 和右侧元素乘积 (`r[i]`) 的乘积。
public class Solution {
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] res = new int[n];
int[] r = new int[n];
int[] l = new int[n];
Arrays.fill(r, 1);
Arrays.fill(l, 1);
for (int i = 1; i < n; i++) { // 预处理l[i],表示i左侧的所有元素的乘积
l[i] = l[i - 1] * nums[i - 1];
}
for (int i = n - 2; i >= 0; i--) { // 预处理r[i],表示i右侧的所有元素的乘积 i+1<n => i < n-1 => i= n-2
r[i] = r[i + 1] * nums[i + 1];
}
for (int i = 0; i < n; i++) { // 枚举计算每一个位置的乘积之和(左边*右边)
int left = 1, right = 1;
if (i > 0) left = l[i];
if (i + 1 < n) right = r[i];
res[i] = left * right;
}
return res;
}
}
LeetCode 2909. 元素和最小的山形三元组 II
1. **初始化**: 使用两个数组 `l` 和 `r` 记录每个位置左侧和右侧的最小值,并初始化结果变量 `res`。
2. **预处理最小值**:
- 从左向右更新 `l` 为左侧元素的最小值。
l[i] = Math.min(l[i - 1], nums[i - 1])
- 从右向左更新 `r` 为右侧元素的最小值。
r[i] = Math.min(r[i + 1], nums[i + 1])
3. **计算结果**:
- 遍历数组,对于每个位置 `j`,检查 `l[j]` 和 `r[j]` 是否小于 `nums[j]`。
- 如果是,更新 `res` 为 `l[j] + nums[j] + r[j]` 的最小值。
4. **返回最终结果**:
- 如果 `res` 没有更新,则返回 `-1`;否则返回 `res`。
public class Solution {
public int minimumSum(int[] nums) {
int n = nums.length;
int[] l = new int[n];
int[] r = new int[n];
Arrays.fill(l, Integer.MAX_VALUE);
Arrays.fill(r, Integer.MAX_VALUE);
int res = Integer.MAX_VALUE;
for (int i = 1; i < n; i++) { // 预处理l[i],表示i左侧元素的最小值
l[i] = Math.min(l[i - 1], nums[i - 1]);
}
for (int i = n - 2; i >= 0; i--) { // 预处理r[i],表示i右侧元素的最小值
r[i] = Math.min(r[i + 1], nums[i + 1]);
}
for (int j = 1; j < n - 1; j++) { // 枚举三元组(i,j,k)中的j
if (l[j] < nums[j] && r[j] < nums[j]) {
res = Math.min(res, l[j] + nums[j] + r[j]);
}
}
return (res == Integer.MAX_VALUE) ? -1 : res;
}
}
LeetCode 1186. 删除一次得到子数组最大和
解法一:前后缀分解+分类讨论
分类讨论:题目分为删除?或不删除两类。
前后缀分解 : 枚举arr[i] , 将子数组和就分为两部分,一个是区间[0,i-1]和pre[i-1],一个是区间[i+1,n-1]和after[i+1],
前者为以i-1结尾最大子数组和(即LeetCode 53。最大子数组和) ,
后者刚好与之相反转化为以i+1开头的最大子数组和,
最后删除一次得到子数组最大和的结果则为 pre[i-1]+after[i+1].
具体来说分为两步:
步骤一:after[i]:包括下标i(以nums[i]为开头)的最大子数组和为after[i]。pre[n] = 0 下标为n开头的最大连续子序列和初始化为0(所以after要开n+1)状态方程 : after[i] = max(after[i-1],0)+arr[i]确定遍历顺序: 从后往前步骤二:pre[i] : 包括下标i(以nums[i]为结尾)的最大子数组和为pre[i]。pre[0] = arr[0] 下标为0结尾的最大子数组和初始化为0状态方程 : pre[i] = max(pre[i-1],0)+arr[i]确定遍历顺序: 从前往后最后正向遍历 ,此时可以同时计算pre[i](步骤二)和计算 pre[i-1]+after[i+1].
package com.coedes.presum.likou1186;
import java.util.Arrays;
/**
* @description:https://leetcode.cn/problems/maximum-subarray-sum-with-one-deletion/description/
* @author: wenLiu
* @create: 2024/4/18 17:45
*/
public class LiKou1186 {
public int maximumSum(int[] arr) {
int n = arr.length;
int[] after = new int[n + 1]; // 以 arr[i] 开头的子数组最大和
Arrays.fill(after, Integer.MIN_VALUE/2);
int res = Integer.MIN_VALUE;
for (int i = n - 1; i >= 0; i--) {
after[i] = Math.max(after[i + 1], 0) + arr[i];
res = Math.max(res, after[i]);
}
int pre = 0;//压缩pre[i]
for (int i = 0; i < n; i++) {
res = Math.max(res, pre + after[i + 1]); // 删除 arr[i] 的区间最大和
pre = Math.max(0, pre) + arr[i];
}
return res;
}
}
解法二:动态规划
2023 美团-南北对决
题目描述
- 武者及属性:参加比赛的武者共有n名,按顺序编号为1到n,他们的战斗力属性也与编号相对应(第i名武者的战斗力属性为i)。
- 派系和胜利规则:
- 如果两名武者来自不同的派系,在擂台上相遇,战斗力属性值大的获胜。
- 如果两名武者来自相同的派系,在擂台上相遇,战斗力属性值小的获胜。
- 决斗次数:所有参赛的武者都会两两进行一场决斗。
- 计算获胜次数:需要计算每名武者获胜的次数
输入描述
单个测试用例包含多组数据输入第一行为一个整数 T ,表示有 T组测试样例。
样例
输入
3 9 0 0 1 0 0 1 0 0 1 6 1 1 0 1 1 0 4 1 0 0 0
输出
5 4 4 4 3 5 3 2 6 3 2 3 2 1 4 0 3 2 1
方法一:暴力法 中心扩散
package com.coedes.presum.meituan20230513T2;
import java.util.Scanner;
/**
* @description:https://codefun2000.com/p/P1287
* @author: wenLiu
* @create: 2024/4/18 22:05
*/
public class MeiTuan202305132 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int T = scanner.nextInt();
// 遍历每个测试用例
while (T-- > 0) {
helper(scanner);
}
}
private static void helper(Scanner scanner) {
int n = scanner.nextInt();
int[] a = new int[n];
for (int i = 0; i < n; i++) {
a[i] = scanner.nextInt();
}
int[] res = new int[n];
for (int i = 0; i < n; i++) {
int l = i - 1, r = i + 1;
int cnt = 0;
int type = a[i];
//中心扩散
while (l >= 0) {
if (type != a[l]) cnt++;
l--;
}
while (r < n) {
if (type == a[r]) cnt++;
r++;
}
res[i] = cnt;
}
for (int i = 0; i < res.length; i++) {
if (i==res.length-1) {
System.out.print(res[i]);
}else {
System.out.print(res[i]+" ");
}
}
System.out.println();
}
}

time out!
方法二:前后缀分解
对于当前武者ai,他能战胜左边不同派系武者和右边相同派系武者
通过从后往前遍历记录 右边相同派系武者数量的后缀和
因为有两个派系 故需要二维数组记录[i,n-1]的后缀和
f[i][0] : [i,n-1] 派系为0的个数
f[i][1] : [i,n-1] 派系为1的个数
初始化: f[n][0] = f[n][1] =0;
递推公式: 回想下一维后缀数组递推式 f[i] = f[i+1] + a[i] <=> f[i] = f[i+1] ; f[i]+=a[i]
f[i][0] = f[i+1][0] ;
f[i][1] = f[i+1][1] ;
f[i][a[i]]++;
前缀和在遍历元素同时一起维护 , 因此只需要一维数组即可 pre = new int[2]; pre[0] 、 pre[1] 分别表示[0,i) 派系为0或者1的个数。
最后 遍历ai
cnt[i] = pre[1-a[i]] +f[i+1][a[i]]; // 左边不同派系武者数量+右边相同派系武者数量
pre[a[i]]++;
package com.coedes.presum.meituan20230513T2;
import java.util.Scanner;
/**
* @description:https://codefun2000.com/p/P1287
* @author: wenLiu
* @create: 2024/4/18 22:05
*/
public class MeiTuan202305132 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int T = scanner.nextInt();
// 遍历每个测试用例
while (T-- > 0) {
solve(scanner);
}
}
//前后缀
private static void solve(Scanner scanner) {
int n = scanner.nextInt();
int[] a = new int[n];
int[][] f = new int[n + 1][2];
// 读取数组 w
for (int i = 0; i < n; i++) {
a[i] = scanner.nextInt();
}
// 从后向前遍历数组 w,更新数组 f
for (int i = n - 1; i >= 0; i--) {
f[i][0] = f[i + 1][0];
f[i][1] = f[i + 1][1];
f[i][a[i]]++;
}
int[] pre = new int[2];
// 遍历数组 w,计算每个位置的 cnts(与后面不同类型的元素数量之和)
for (int i = 0; i < n; i++) {
int type = a[i];
int cnts = pre[1 - type] + f[i + 1][type];
pre[type]++;
System.out.print(cnts + " ");
}
// 换行,处理下一个测试用例
System.out.println();
}
}
给定一个长度为 n 的整数序列 a1, a2,...,an 和一个整数 k。
请你计算有多少个三元组(x,y,z)同时满足以下所有条件.
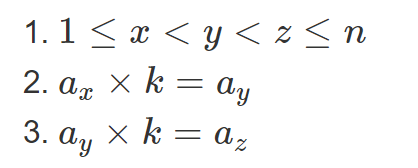
输入格式
一个整数,表示满足所有条件的三元组的数量。
数据范围
暴力美学(一定超时滴)
//暴力
public static int countTriplets(int[] a, int k) {
int count = 0;
int n = a.length;
// 使用三重循环遍历所有可能的三元组 (x, y, z)
for (int x = 0; x < n - 2; x++) {
for (int y = x + 1; y < n - 1; y++) {
for (int z = y + 1; z < n; z++) {
// 检查是否满足条件 a[x]*k == a[y] && a[y]*k == a[z]
if (a[x] * k == a[y] && a[y] * k == a[z]) {
count++;
}
}
}
}
return count;
}
机器学习的特征工程里面经常涉及降维处理,在算法和数据量都确定情况下,对数据进行处理尤为重要,例如可通过皮尔森系数画出热力图排除掉相关系数接近1的特征值,实现数据降维,提高模型计算速度....
1. 分析超时原因:
- 暴力法的时间复杂度为 O(n3)。
2. 降维转化为二元组问题:
- 将三元组 (x,y,z)转化为二元组问题,即寻找满足关系 ax = ay/k和 az = ay * k的二元组。
3. 转化条件:
- 根据条件 ax = ay/k 和 az = ay * k,发现 ax和 az都与 ay 有关,可表示为 ax = ay/k 和 az = ay * k。
4. 优化方法:
- 使用哈希表(Map)进行优化,具体步骤如下:
构建两个哈希表:
使用 `map1` 存储左侧元素,`map2` 存储右侧元素。
遍历 数组:
对于每个 ay,通过哈希映射找到 `map1` 中 key 为 ay/k(注意这里需要保证 ay 是k 的整数倍)和 `map2` 中 key 为 ay * k的元素,然后计数满足条件的二元组数量。
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int k = scanner.nextInt();
long[] a = new long[n];//题目数据范围>10^8
Map<Long, Integer> map1 = new HashMap<>();//保存左边元素及其出现次数
Map<Long, Integer> map2 = new HashMap<>();//保存右边元素及其出现次数
for (int i = 0; i < n; i++) {
a[i] = scanner.nextLong();
map2.put(a[i],map2.getOrDefault(a[i],0)+1);
}
long res = 0;
for (int i = 0; i < n; i++) {
long ay = a[i];
map2.put(ay, map2.get(ay) - 1);
if (ay % k == 0) {
long ax = ay / k;
long az = ay * k;
res += (long) map1.getOrDefault(ax, 0) * map2.getOrDefault(az, 0);
}
map1.put(ay,map1.getOrDefault(ay,0)+1);
}
System.out.println(res);
}
题目描述
给定一个长度为n的数组,通过合并相邻元素一次,使得数组的极差(数组最大值和最小值的差)尽可能小。
合并操作:选择两个相邻元素合并成一个,新元素为原两元素之和。
最终目标:使得数组的极差最小化。
输入描述
输入
第一行为一个整数 n,表示数组的长度。
输入第二行为 n 个整数,第i个整数为 ai . 2<n< 105, 1<ai < 109
(ps:如果1<n< 105那最多只能使用 O(nlogn)的算法去求解,如果1 ≤ ai≤ 109 要开long!)
输出描述
一个整数,代表操作后的极差最小值。
input
100
2 8 1 99 77 16 8 7 69 52 6 34 46 17 37 81 99 63 26 83 68 32 78 38 69 91 47 34 69 98 41 75 80 54 51 36 81 85 78 67 17 100 20 30 54 16 30 93 83 31 98 12 70 51 58 80 64 3 45 57 7 56 100 45 99 62 76 34 90 25 47 81 67 9 10 20 14 95 30 78 49 46 93 88 25 63 8 6 37 93 66 79 47 41 45 18 28 54 63 17
output
98
题解:前后缀分解+分类讨论
- 使用预处理的后缀数组计算右边部分的最大值和最小值。
- 枚举合并区间:对于数组中的每个位置 i (i∈[1,n-1]),考虑合并区间 [i, i+1],计算合并后的最大值和最小值。
- 区间划分:将数组划分为三部分:左边部分 [1, i-1]、合并区间 [i, i+1]、右边部分 [i+2, n]。
- 动态更新左边部分的最大值和最小值:从前往后遍历,维护变量 `pre_min` 和 `pre_max`。
计算极差:对于每个 i,计算左、合并和右三部分的最大值和最小值,然后计算极差,更新最小极差。
package com.coedes.presum.mayi2023;
import java.util.*;
/**
* @description:https://codefun2000.com/p/P1242
* @author: wenLiu
* @create: 2024/4/19 10:55
*/
public class Mayi202304201 {
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
// 读取数组长度
int n = scanner.nextInt();
// 读取数组元素
int[] arr = new int[n + 1];
for (int i = 1; i <= n; i++) {
arr[i] = scanner.nextInt();
}
// 调用函数计算最小极差
int result = minimizeDifference(n, arr);
// 输出结果
System.out.println(result);
scanner.close();
}
public static int minimizeDifference(int n, int[] arr) {
// 使用预处理的后缀数组计算右边部分的最大值和最小值。
int[] postMax = new int[n + 2]; // i ∈ [1,n] 最后一位n+1用于初始化 0 不存元素
int[] postMin = new int[n + 2];
postMax[n] = Integer.MIN_VALUE;
Arrays.fill(postMin, Integer.MAX_VALUE);
for (int i = n ; i >= 1; i--) {
postMax[i] = Math.max(postMax[i + 1], arr[i]);
postMin[i] = Math.min(postMin[i + 1], arr[i]);
}
int ans = Integer.MAX_VALUE;
int preMin = Integer.MAX_VALUE, preMax = Integer.MIN_VALUE;
for (int i = 1; i < n; i++) {
int merge = arr[i] + arr[i + 1];
if (i > 1) {
preMin = Math.min(preMin, arr[i-1]);
preMax = Math.max(preMax, arr[i-1]);
}
// 计算极差:对于每个 i,计算左、合并和右三部分的最大值和最小值,然后计算极差,更新最小极差。
int max = Math.max(Math.max(preMax, merge), postMax[i + 2]);
int min = Math.min(Math.min(preMin, merge), postMin[i + 2]);
ans = Math.min(ans, max - min);
}
return ans;
}
}
给定一个字符串 s,字符串中包含多少个 red 子串,就给这个字符串一个权值,权值就是 red 子串的数量。
例如:redd 权值为1,redredr 权值为2,reed 权值为0
现在考虑计算一个字符串s所有非空子序列的权值和。答案可能很大,请对1e9 +7取模
输入描述
输入第一行为一个字符串s(1 <|s|< 100000)
输出描述
输出字符串所有非空子字符串的权值和。
题解:
字符串子序列:
一个字符串的子序列是从原始字符串中删除零个或多个字符(不改变其相对顺序)而不包括空字符串和整个字符串本身。
对于字符串 "redd",所有非空子序列包括:
1. 单个字符的子序列:'r', 'e', 'd', 'd'
2. 两个字符的子序列:'re', 'rd', 'rd', 'ed', 'dd'
3. 三个字符的子序列:'red', 'red', 'red', 'edd'
4. 四个字符的子序列:'redd'
因此,字符串 "redd" 的所有非空子序列为:
'r', 'e', 'd', 'd', 're', 'rd', 'rd', 'ed', 'dd', 'red', 'red', 'red', 'edd', 'redd'
子序列公式推导:
在计算字符串的子序列数量时,可以使用组合数学的概念来理解和计算。一个字符串的子序列是从原始字符串中删除零个或多个字符(不改变其相对顺序)而不包括空字符串和整个字符串本身。
回到题目,题目要求计算一个字符串 s 所有非空子序列的权值和,
1. 字符串子序列分为三部分:
- 字符串 s 的子序列可以分为三部分:以字符 'r' 结尾的部分 si...r、'e'、以字符 'd' 开头的部分 d...sj,表示为 si..r...e...d...sj。
2. 定义辅助数组:
- 定义数组 r[i] 表示以字符 'r' 结尾的子序列的数量,定义数组 d[i] 表示以字符 'd' 开头的子序列的数量。
- 对于 r[i],考虑以 si...r 结尾的子序列数量,对于 d[i],考虑以 d...sj 开头的子序列数量。
3. 计算数量:
- 对于 r[i],根据字符串长度 i,子序列数量为 2i。
- 对于 d[i],根据字符串长度 n和字符位置 i,子序列数量为 2n-i-1。
4. 使用辅助数组 p[]:
- 定义数组 p[i] 来存储 2i 的结果,初始化 p[0] = 1。
- 这样可以减少重复计算 2i的时间损耗。
5. 求解结果 res:
- 对于字符串中的每个字符 'e',根据其位置 i,计算以当前位置 i 的 r[i] 和 d[i] 的乘积,即 res = r[i] *s d[i]。
package com.coedes.presum.mayi202304043;
import java.util.Scanner;
/**
* @description:https://codefun2000.com/p/P1158
* @author: wenLiu
* @create: 2024/4/19 14:18
*/
public class Mayi202304043 {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
String s = in.nextLine();
System.out.println(helper(s));
}
private static long helper(String s) {
int n = s.length();
final long mod = 1000000007;
long res = 0;
long[] p = new long[n + 1];
p[0] = 1;
for (int i = 1; i < p.length; i++) {
p[i] = (p[i - 1] * 2) % mod;
}
long[] d = new long[n + 1];
for (int i = n - 1; i >= 0; i--) {
d[i] += d[i + 1];//更新数组
char c = s.charAt(i);
if (c == 'd') {
d[i] = (d[i] + p[n - i - 1]) % mod;
}
}
long pre = 0;
for (int i = 0; i < n; i++) {
char c = s.charAt(i);
if (c=='r') {
pre = (pre + p[i])%mod;
}
if (c=='e') {
res = (res + (pre*d[i])%mod)%mod;
}
}
return res;
}
}
可以修改数组中的任意一个元素,将其修改为任意值。个他希望用最少的操作方式使得数组满足以下条件:
1.最终数组仍是一个排列。
2.最终数组的逆序对数量为 1。
数组的逆序对是指,满足i< j且 ai> aj, 的二元组数量
排列指长度为 n 的数组, 1 到 n 每个正整数恰好出现 1 次。
输入描述
第一行输入一个正整数 n ,2 ≤n ≤ 105 代表数组的大小。
第二行输入几 个正整数 a ,1≤ai≤n
保证初始数组是一个排列。
样例
输入
样例一:
4 3 2 1 4
输出
3
题解 : 前后缀
1、由于数组是排列因此先替换数组元素 使得元素升序排列1 2 3 ...n
2、枚举二元组(i,i+1) 1<=i<n ,将数组分为[1,i-1] [i,i+1] [i+2,n] , 计算维护1...i-1 升序序列 替换次数 + 维护i、i+1逆序对替换次数+ 维护i+2...n升序序列替换次数。
import java.util.Scanner;
/**
* @description:from https://codefun2000.com/p/P1054
* @author: wenLiu
* @create: 2024/4/19 15:12
*/
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] a = new int[n + 1];
for (int i = 1; i <= n; i++) {
a[i] = in.nextInt();
}
int[] s = new int[n + 2];
for (int i = n; i >= 1; i--) {
s[i] = s[i + 1] + (a[i] == i ? 0 : 1);
}
int pre = 0;
int res = Integer.MAX_VALUE;
for (int i = 1; i < n; i++) {
if (i > 1) {
pre = pre + (a[i - 1] == i - 1 ? 0 : 1);
}
int cnt = 0;
if (a[i] != i + 1) {
cnt++;
}
if (a[i + 1] != i) {
cnt++;
}
res = Math.min(res, pre + cnt + s[i + 2]);
}
System.out.println(res);
}
}
思路 : 二分答案+双指针
package com.coedes.binary_search.likou1482;
import java.util.Arrays;
/**
* @description:https://leetcode.cn/problems/minimum-number-of-days-to-make-m-bouquets/
* @author: wenLiu
* @create: 2024/4/29 22:01
*/
public class Solution {
public static void main(String[] args) {
//bloomDay = [1,10,2,9,3,8,4,7,5,6], m = 4, k = 2
int[] bloomDay = {1, 10, 2, 9, 3, 8, 4, 7, 5, 6};
int m = 4, k = 2;
System.out.println(new Solution().minDays(bloomDay, m, k));
}
public int minDays(int[] bloomDay, int m, int k) {
//题目问:请你返回从花园中摘 m 束花需要等待的最少的天数。 那就设 摘 m 束花需要等待的最少的天数为x填...
// m(x) 表示 摘 m 束花与等待天数x函数 , 显然m(x) 随着 x 递增而递增... 考虑二分答案...
int n = bloomDay.length;
if ((long) m * k > n) return -1;
// x ∈ [1, max(bloomDay)]
int l = 1, r = Arrays.stream(bloomDay).max().getAsInt();
while (l < r) {
int mid = l + (r - l) / 2;
if (check(mid, m, k, bloomDay)) {
r = mid;
} else {
l = mid + 1;
}
}
return r;
}
private boolean check(int mid, int m, int k, int[] bloomDay) {
int n = bloomDay.length;
int res = 0;
for (int i = 0; i < n - k + 1; i++) {
int j = i, cnt = 0;
while (j < n && bloomDay[j] <= mid && cnt < k) {
cnt++;
j++;
}
/*
这样写会导致死循环 bloomDay = [1,10,2,9,3,8,4,7,5,6]
j = 1 bloomDay[1] > mid false
=> i = j-1 = 0 =>
for i++
=> j =1 bloomDay[1] > mid false => .... 死循环
if (cnt == k) {
res++;
}
i = j - 1;*/
if (cnt == k) {
res++;
i = j - 1;
}else {
i = j;//此时 bloomDay[j] > mid i=j++;
}
}
return res >= m;
}
}
LeetCode 2528. 最大化城市的最小供电站数目
题解:二分答案+前缀和+差分数组+贪心(好家伙四大天王组合拳...疼哭了...)参考灵茶山艾府题解
[最小电量的最大值] => 最小值最大化问题 => 二分答案 => l = min(station[i]) , r = max(station[i]+k+1) mid = (l+r+1)/2
从左到右遍历 &amp;amp;amp;amp;amp;amp;amp;amp;amp;lt;span class="katex"&amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;&amp;amp;amp;amp;amp;amp;amp;amp;amp;lt;span class="katex-mathml"&amp;amp;amp;amp;amp;amp;amp;amp;amp;gt;stations,如果station[i] 不足mid ,则需要在当前位置i开始的后[i,i+2*i]加上(mid-station[i]) =&amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt; 区间求和问题 =&amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt; 差分 =&amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt; 回忆下差分 [l,r]+val =&amp;amp;amp;amp;amp;amp;amp;amp;amp;amp;gt; d[l]+val d[r+1]-val
&amp;amp;amp;amp;amp;amp;amp;amp;amp;nbsp;


