最小高度树

最小高度树

题目出处:
https://leetcode-cn.com/problems/minimum-height-trees/

目标

对于一个具有树特征的无向图中, 找出一个根节点, 使的构成的树高度最小.

上图:

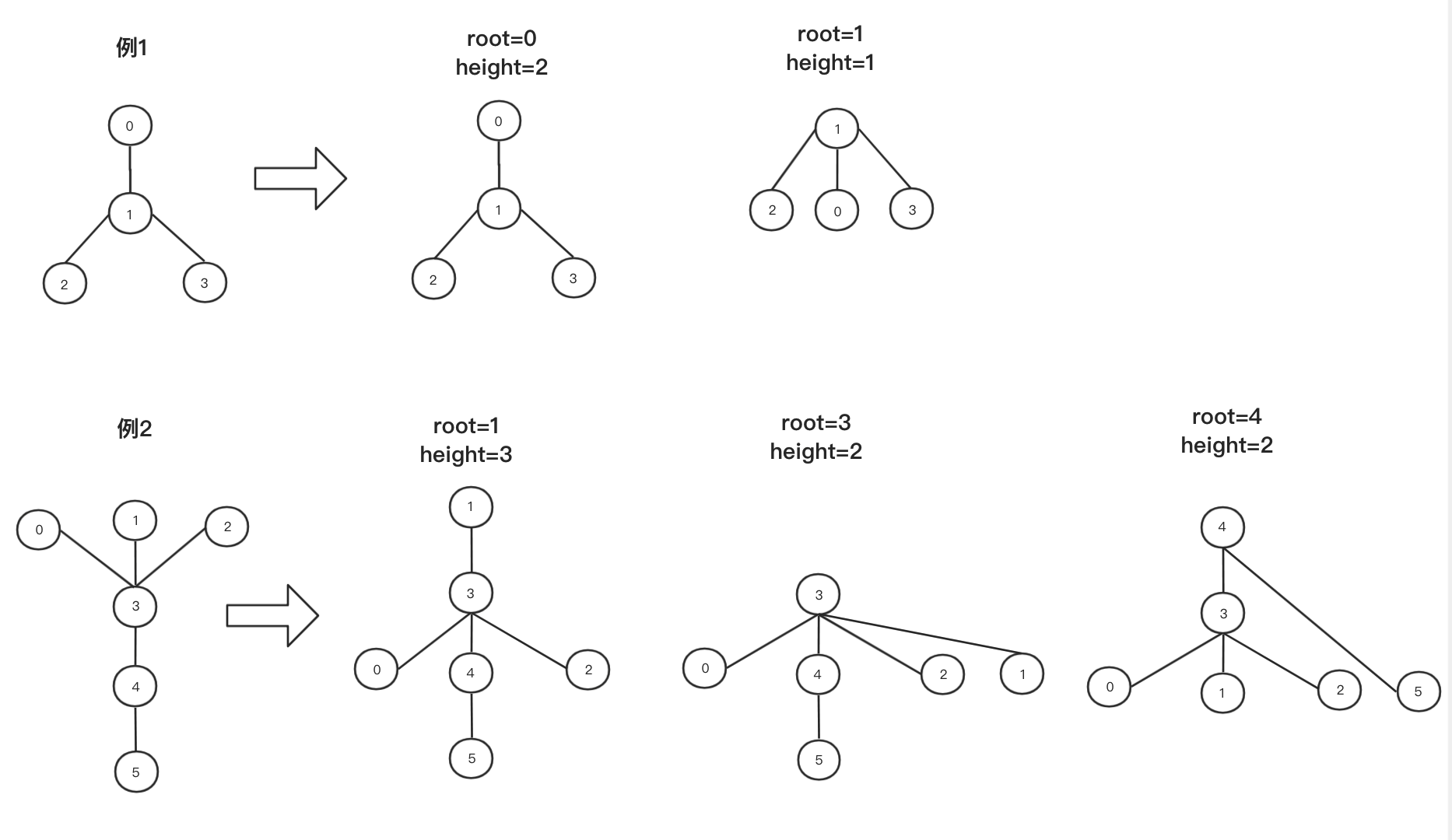
第一个例子中,只有以 1 为 root 时高度为 1,以 0,2,3 为 root 时高度均为 2,所以需要返回结果[1]

第二个例子中,以 3 和 4 为 root 时高度均为 2,其它情况下都大于 2,所以结果为[3,4]

分析

树的高度指什么?

h = max([dist(root,leaf) for leaf in nodes])

即: 从根节点到所有叶子节点的高度最大值.

为了使生成的树的高度最小,root 节点必须是尽可能接近中心的.

如何理解中心?

• 将只有一条边连接的节点定义为叶子节点,中心节点可以理解为离所有叶子节点都相对较近的点.

如何找出中心节点?

• 如果将最外层叶子节点砍掉,就会有新的一层叶子节点出现,这样一直砍下去直到最后一层就是中心节点.

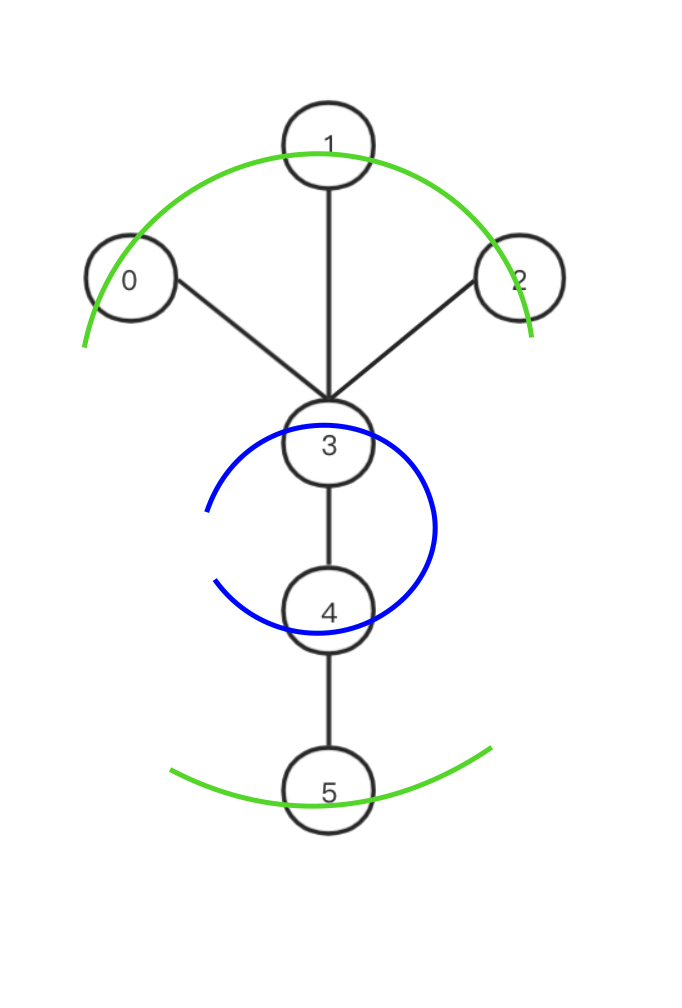
例如下面第一张图中,叶子节点是0,1,2,5,将0,1,2,5砍掉后,叶子节点为3,4,此时没有非叶子节点了,3,4就是我们要求的点. 第二张图中,砍掉最外层叶子节点0,1,2,7,8,9,11后,3,6,10变成了叶子节点,砍掉3,6,10后,4,5变成了叶子节点,此时没有非叶子节点了,4,5就是我们要求的点.

代码实现

class Solution(object):
    def findMinHeightTrees(self, n, edges):
        """
        :type n: int
        :type edges: List[List[int]]
        :rtype: List[int]
        """
        # 思路:
        # 从最外层遍历,最后一层即为结果.

        if n == 1:
            return [0]

        # 构造邻接表和度
        adjs = defaultdict(list)
        degrees = [0 for _ in range(n)]
        for (f, t) in edges:
            adjs[f].append(t)
            adjs[t].append(f)
            degrees[f] += 1
            degrees[t] += 1

        # BFS
        # 第一层(最外层)
        layer = []
        for ind, val in enumerate(degrees):
            if val == 1:
                layer.append(ind)
        # 层层缩进:遍历当前层,确定下一层节点.
        while layer:
            next_layer = []
            for node in layer:
                for neighbor in adjs[node]:
                    degrees[neighbor] -= 1
                    if degrees[neighbor] == 1:
                        next_layer.append(neighbor)
            if not next_layer:  # 下一层没东西了,说明当前遍历的最后一层,也就是我们需要的
                return layer
            layer = next_layer